高木曲線は [0,1] 区間で長さ無限大
前回の記事で、高木関数が連続であることと高木関数が至る所微分不可能であることを紹介しました。今回は高木関数の長さについて考えてみましょう。
高木関数って何だっけ?
三角波関数
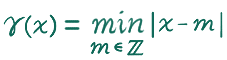
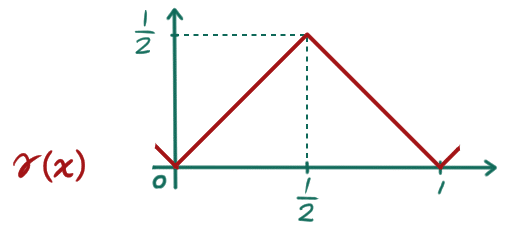
に対して、それを(原点を中心に)1/2 倍に縮小した関数
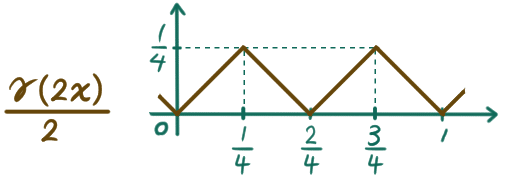
を考え、更に 1/4 倍に縮小した関数
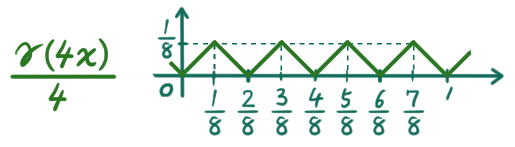
を考え、更に 1/8 倍に……というようにどんどん縮小した関数を考えて、それらを全部足して作られる関数
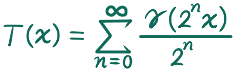
が高木関数でした。グラフは、はじめは(n=0 までの和)
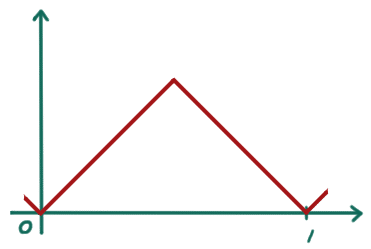
となっていたのが、次の n=1 までの和は
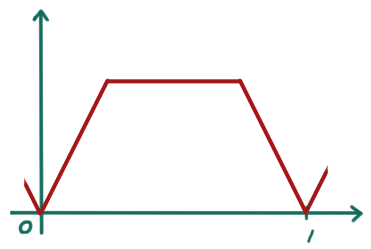
となって、次の n=2 までの和は
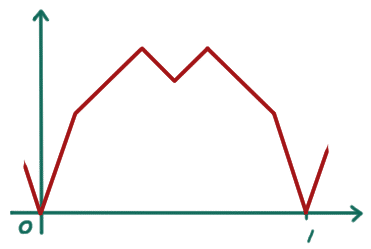
となって、次の n=3 までの和は
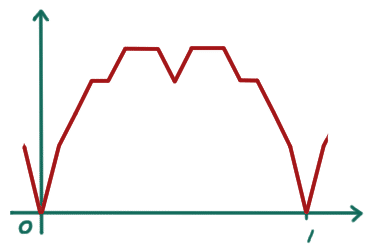
こうなって、っていうのを繰り返して、最終的には
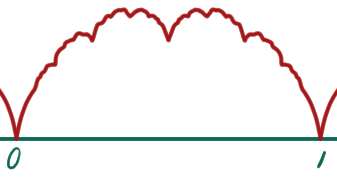
こんな感じのモコモコしたグラフになるのでしたね。これは至る所連続なのに至る所微分不可能という奇妙な性質を持っているのでした。
↓ 動画

高木関数の長さ
結論から言うと、有限区間での高木関数の長さは無限大です。簡単に示せるかなーと思ったらなかなか難しい。この記事は
J. C. Lagarias. The Takagi function and its properties. arXiv preprint arXiv:1112.4205. (2011)
の論文(Theorem 11.4)の証明のアイデアを参考にしています。
まず、[0,1] 区間で高木関数の長さが無限大になることを見ましょう。高木関数を作る過程の折れ線状のグラフは、ステップが進むごとにまっすぐだったところをどんどん折っていくので、ステップが進むと長さが増えるというのはすぐにわかりますね。さて、その折れ線状のグラフの傾きに着目してみましょう。最初の
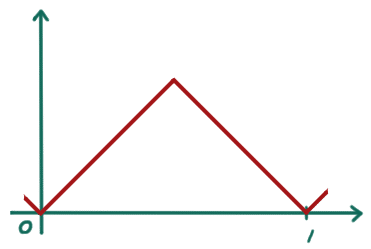
の傾きは、[0,1] 区間を2等分にして左から順に
1 -1
となっていますね。次の
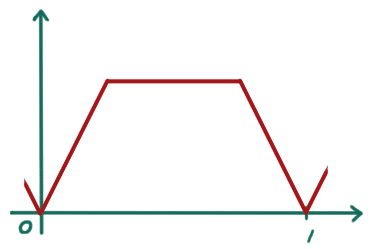
の傾きは、[0,1] 区間を4等分にして左から順に
2 0 0 -2
となっています。次の
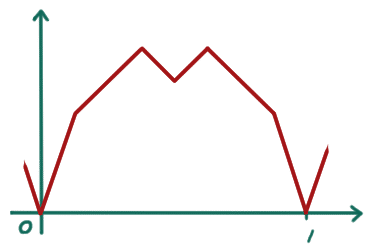
の傾きは、[0,1] 区間を8等分にして左から順に
3 1 1 -1 1 -1 -1 -3
となっています。規則性にお気づきでしょうか? 勘の良い方は次の図が思い浮かぶでしょう。

一番上の 0 から出発して、赤の道が左下に、青の道が右下に続いています。赤の道に進むと 1 を足して、青の道に進むと 1 引きます。そうやってどんどん枝を増やして作られる整数の並びが、高木関数を作る途中のグラフの傾きの並びになっているんですね。
さて、この図で 0 だけやたら目立たせていますね。傾きが 0 の区間が現れると何が起こるでしょうか?

このように、x 軸に平行な部分は、次のステップで

こんな風に、傾き 1 と -1 のギザギザになります。ある時点の傾き 0 の区間の長さの総和が L であれば、その部分の長さは次のステップで (√2)L になりますね。つまり、傾き 0 の区間は、次のステップで長さが (√2)-1 倍になるんです。
さて、傾き 0 の区間は、いつ、どれくらい現れるでしょうか? 先ほどの樹形図をみるとわかる通り、0 が現れるのは n が奇数のときですね。個数はどうでしょうか? 0 が現れる経路は
赤の道の数=青の道の数
の経路ときなので、n = 2k - 1 番目のとき、2k 本の道から k 本選ぶ選び方、すなわち
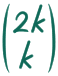
個の区間だけ 0 が現れます。n = 2k - 1 番目において一つ分の区間の長さは 1/(2^(2k)) なので、傾き 0 の区間の長さの総和は
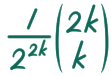
ですね。奇数番目から偶数番目にグラフが変化するごとに、長さは少なくともこの値 × ((√2)-1) は増加することがわかります。したがって考えるべき問題は

です。これが発散すれば、高木関数の [0,1] 区間における長さが無限大になることがわかりますね。この手の発散を調べるには、階乗を近似するスターリングの近似(Stirling's approximation)が有効です。ある正定数 C_1, C_2 が存在して、
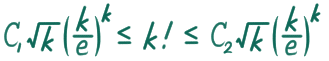
が成り立つというものです。これを使うと、ある正定数 C によって
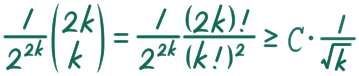
と下から評価でき、1/√k は級数を取ると発散するので( 1/√k ≧ 1/k )、元の級数も発散することがわかります。したがって高木関数の [0,1] 区間における長さが無限大になることがわかりました!
なお、[0,1] 区間に限らず、どんな区間 [x_1, x_2] (x_1 < x_2) を取っても、n をどんどん増やしていけばそのうち傾き 0 の折れ線が [x_1, x_2] の中に現れるので、同様の議論で任意の区間 [x_1, x_2] における高木関数の長さが無限大になることもわかります。
―・―・―・―・―・―・―・―・―・―・―・―・―・―・―・―・―
【爽籟 蜜柑(そうらい みかん)】
数学記事書いてる人。→ ブログ
Youtube チャンネル ↓
―・―・―・―・―・―・―・―・―・―・―・―・―・―・―・―・―