トマエ関数がいたる所微分不可能であることの証明
トマエ関数(Thomae's function)。別名ポップコーン関数。実数から実数への関数なんですが、有理数の点では不連続でありながら、無理数の点では連続という変な関数です。
ただこの性質自体は、微分積分学の教科書の演習問題にしょっちゅう出てくるし、ネット上でもいろんな人によって解説されてます。かくいう私もYoutubeで説明してたり...
無駄に編集凝ってるので見てくれるとうれしみ。
で、この記事では連続性については横に置いといて、トマエ関数の「至る所微分不可能」という性質について見てみようと思います。
以前、高木関数の記事を書きましたが、高木関数は至る所連続で至る所微分不可能という変な関数でした。一方、トマエ関数は無理数の点だけで連続で至る所微分不可能という変な関数です。不連続点が多い分驚きが小さいかもですが、まあ、証明を検索しても日本語の記事が見当たらなかったので補完の意味も込めて一応この記事を書いとこうかと。
(いやほんとはこの性質も含めてトマエ関数のいろんな性質を動画化しようと思って途中まで作ってたんですが結局没にして、でも捨てるのがもったいなかったのでnoteに上げとこかなという側面も……まあいいんですよそんな話は)
今日の話を1枚にまとめると

こんな感じ。では解説。
そもそもトマエ関数って何だっけ?
トマエ関数Tは、実数を受け取り、実数を返す関数で、次のように定義されます。

要は、入力された実数 x が無理数なら 0 を返して、x が 0 なら 1 を返して、x が有理数なら、xを既約分数として書いたときの分母(分母が正になるように取る)を q として 1 / q を返します。
例えば T(π) = 0, T(0) = 1, T(- 3 / 4) = 1 / 4 といったかんじ。
グラフを書くと、

こんな感じになります。ポップコーンがポンポンはねてるみたいだからポップコーン関数というそうな。この関数が、有理数の点で不連続で、無理数の点で連続という変な性質を持っているのです。以下、その性質はご存じ、ってことにして、話を続けます。
有理数の点で微分不可能であること
まずは有理数の点で微分不可能であることを見てみましょう。といっても、すでに有理数の点で不連続ってのがわかってるので、基本的な定理

の対偶取って一瞬ですね。おわり。
無理数の点で微分不可能であること
今日のメイン。まずは
![]()
しておきましょうか。目標は

ですね。極限の非存在を示すには、極限の存在の反例となるような数列を取るのがわかりやすくていいですね。つまり、x に収束する数列を2つ取って、それぞれの数列を使って極限を計算して、それらの極限が異なることを示せばいいってことです。つまり、方針としては

ってことです。a_n も b_n も、 x とは異なる値を取るようにしなきゃだめってのに注意です。
じゃあトマエ関数を考えてるこの状況で、「2つの数列をどんなふうに取ればいいの?」ってことですが、まず思いつくのが、x に収束する有理数列と無理数列を取ろうっていう発想ですね。トマエ関数は有理数に対しては正、無理数に対しては 0 っていうわかりやすい違いがあるので、この違いを引き出すことを狙いましょう。ということで、まずは
![]()
とってみよう!
どんなの取ればいいでしょうか? x は既に無理数として固定してましたね。さっきも言った通り a_n = x とするのは無しですよ。じゃあどうするか。少しずらして、

でおっけーですね。これで x に収束する無理数列 a_n ができましたよと。じゃあ
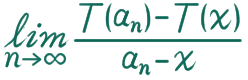
を計算しましょう。といっても、a_n はずっと無理数だし、x も無理数なんだから、簡単ですね。T は無理数に対しては 0 を返す関数なので、
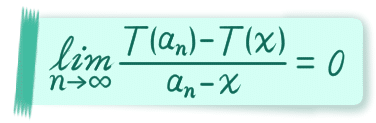
ですね。前半戦終了。次は、
![]()
とってみよう!
x は無理数。無理数に収束する有理数列はいろんな作り方がありますが、一番シンプルなのは (整数)/ n の形での近似ですね。まずこの形で考えてみて、失敗したらその都度調整、って方針でいきましょう(高木関数のときは (整数)/ (2^n) の形で近似してましたね)。

nx の天井関数を n で割ったのを b_n にしましょう。こうすると b_n は有理数で、x と異なる値を取りながら x に収束しますね( x < b_n < x + (1 / n) ではさみうち)。それじゃ、この b_n に対して
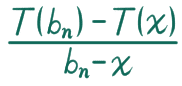
の n → ∞ の極限を考えましょう。
でも...
T(x) = 0 なのはいいんですが、T(b_n) ってなんかよくわかんないんですよね。l_n と n で約分できるかどうかとか考えたくない……。
こんなときにずるいことを考えるのが数学。別に極限ちゃんと求めんでええんちゃう?
無理数列 a_n を使った時の極限は 0 でした。てことは、↑の極限が 0 じゃないってことだけわかればいいですね。例えばある正の(n に依存しない)定数 C があって、常に
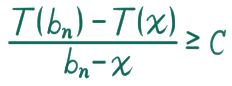
になる、なんてことがわかったら、何に収束するのかは知らない(それどころか収束するかどうかも知らない)けど、少なくとも 0 に収束するなんてことはあり得ない、ってことが言えますね。
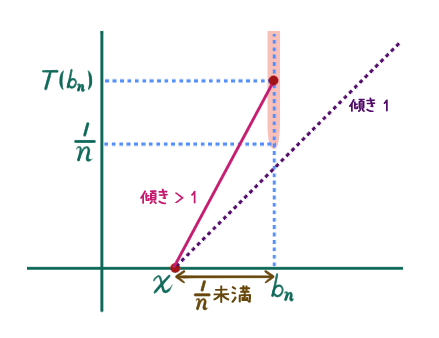
ということで不等式評価! 分子は下から抑えて、分母は上から抑える!
分母は
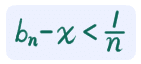
なので、1/n で上から抑えられますね。
次、分子、すなわち T(b_n) を下から抑えたい。今、b_n = l_n / n です。もしこれが既約分数なら T(b_n) =1 / n ですが、既約分数じゃないかもしれない...
既約分数じゃなかったらどうなる? 約分される。つまり n > m となるある正整数 m に対して T(b_n) =1 / m なんてことになるわけですが...
(。´・ω・)ん?
じゃあこのときって、 T(b_n) = 1 / m > 1 / n ってこと……あ、じゃあ、既約分数であろうがなかろうが、結局
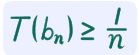
じゃないですか! 下から評価できた! てことで
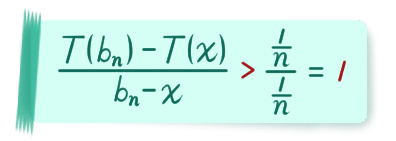
になりました! この左辺が 0 に収束するわけが無かろうて!
イメージとしてはこんな感じ。
ということで、
ある無理数列を使うと、0に収束する。ある有理数列を使うと、0 には収束しない。つまり
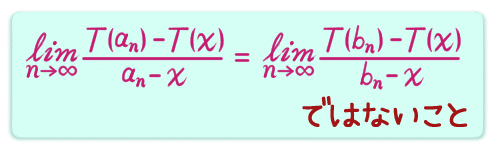
がわかって、トマエ関数が x で微分不可能ってことがわかりました!
x は任意の無理数として取ってたので、無理数の点で微分不可能ってのがわかりましたね。有理数の点でも微分不可能だったので、至る所微分不可能! やったね! おしまい!
―・―・―・―・―・―・―・―・―・―・―・―・―・―・―・―・―
【爽籟 蜜柑(そうらい みかん)】
数学記事書いてる人。→ ブログ
Youtube チャンネル ↓
―・―・―・―・―・―・―・―・―・―・―・―・―・―・―・―・―