九州大文系数学２０２４年解説【［３］答えと否定は分けて考える】

２０２４年の九州大学の入試問題の解説をアップしています。
前回はこちら。

今回第３問です。問題はこちら

今回のセットでは一番難しい問題だったかなと思います。ただ、「答え」は実験で見えてきます。なので、「答え」と「答え以外の否定」は分けて示していくという割り切りが大事だったかなと思います。

（１）
不等式の証明のセオリーである引き算からの証明でいいでしょう。
何が必要かは設定から抽出してきましょう。
（ｂ－１）≧ａならば、（ｂ－１）！≧ａ！は証明なしでいいのではと思います。

（２）
まずは、実験でａ＝１、ｂ＝２がわかりますので、それ以外の答えがないことを示すことを考えていきます。当然（１）を活用することになります。
答えは、設定の条件のａ＜ｂのとき、ｂ！／ａ！≧ｂからｂ＝２が導かれるのですから、ａとｂの場合分けで、残りを否定すればいいのかなと思います。

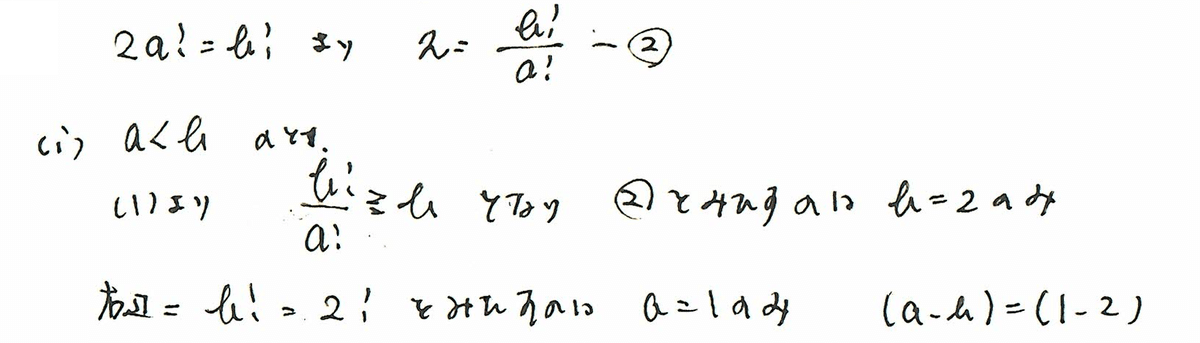
あとは、否定する流れです。

（３）
こちらも実験で答えがわかります。

ａ＝ｂ＝ｃ以外は否定の証明となります。
ａ＜ｂであっても、ａ＞ｂであっても、ｃはその間になるので、

となります。

文理を問わず、九大数学対策において、論証問題は重要だと感じます。
来年度受験生は、論証、整数問題は広く対策が必要だと思います。
この程度の出題ならば、カリキュラム変更には無関係なので、しっかりと演習を積んでおきましょう。