ポートフォリオ理論
ポートフォリオ理論とは、二つ以上の資産を購入する際に、リスクを最小にしてリターンを最も大きくとる購入方法を決定する理論である。
資産が二つ(二つとも有リスク資産)の時のポートフォリオ理論
二つの資産A1、A2について、
収益率 $${R_{1}}$$ $${R_{2}}$$
平均収益率 $${μ_{1}}$$ $${μ_{2}}$$
偏差(リスク) $${σ_{1}}$$ $${σ_{2}}$$
二つの資産の収益率の相関係数 $${ρ}$$
と設定する。
また、各資産を、$${ω_{1}}$$、$${ω_{2}}$$(ただし$${ω_{1}+ω_{2}=1}$$)の割合で購入するとする。
この時、平均収益率$${μ}$$は、
$$
μ=E[ω_{1}R_{1}+ω_{2}R_{2}]=ω_{1}μ_{1}+ω_{2}μ_{2}
$$
偏差は、
$$
\begin{aligned}
σ&=\sqrt{Var[ω_{1}R_{1}+ω_{2}R_{2}]}\\
&=\sqrt{E[((ω_{1}R_{1}+ω_{2}R_{2})-μ)^2]}\\
&=\sqrt{E[((ω_{1}R_{1}+ω_{2}R_{2})-(ω_{1}μ_{1}+ω_{2}μ_{2}))^2]}\\
&=\sqrt{E[((ω_{1}R_{1}-ω_{1}μ_{1})+(ω_{2}R_{2}-ω_{2}μ_{2}))^2]}\\
&=\sqrt{E[(ω_{1}(R_{1}-μ_{1})+ω_{2}(R_{2}-μ_{2}))^2]}\\
&=\sqrt{E[{(ω_{1}}^2(R_{1}-μ_{1})^2+2ω_{1}ω_{2}(R_{1}-μ_{1})(R_{2}-μ_{2})+{ω_{2}}^2(R_{2}-μ_{2})^2]}\\
&=\sqrt{{ω_{1}}^2E[(R_{1}-μ_{1})^2]+2ω_{1}ω_{2}E[(R_{1}-μ_{1})(R_{2}-μ_{2})]+{ω_{2}}^2E[(R_{2}-μ_{2})^2]}\\
&=\sqrt{{ω_{1}}^2{σ_{1}}^2+2ω_{1}ω_{2}ρσ_{1}σ_{2}+{ω_{2}}^2{σ_{2}}^2}\\
&=\sqrt{({ω_{1}}{σ_{1}}+{ω_{2}}{σ_{2}})^2-2ω_{1}ω_{2}σ_{1}σ_{2}(1-ρ)}\\
&=({ω_{1}}{σ_{1}}+{ω_{2}}{σ_{2}})\sqrt{1-\frac{2ω_{1}ω_{2}σ_{1}σ_{2}(1-ρ)}{({ω_{1}}{σ_{1}}+{ω_{2}}{σ_{2}})^2}}
\end{aligned}
$$
9行目から、相関係数ρは1以下であるため、
$$
σ\leqq{ω_{1}}{σ_{1}}+{ω_{2}}{σ_{2}}
$$
となる。以上から、保有割合の変化により、収益率μは線形変化するが、偏差(リスク)σは線形変化より小さい値を取るということが分かる。具体的に、数字を当てはめて計算し、グラフを作成してみると、次のグラフが得られる。凡例の数字は相関係数を示している。
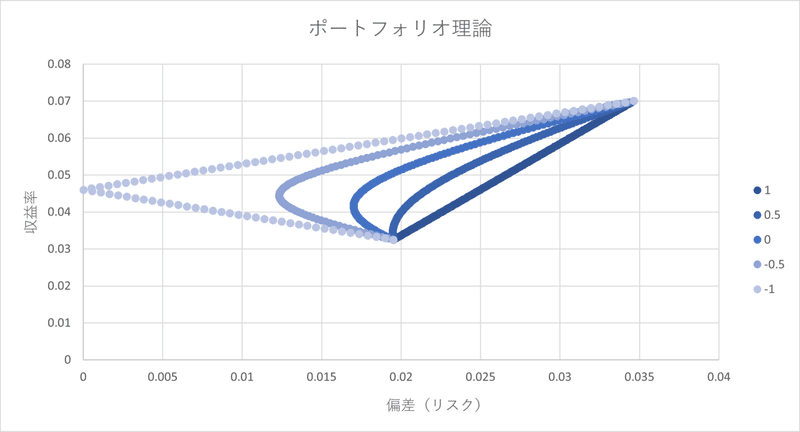
$${ρ=1}$$の場合、
$$
\begin{aligned}
σ&=({ω_{1}}{σ_{1}}+{ω_{2}}{σ_{2}})\sqrt{1-\frac{4ω_{1}ω_{2}σ_{1}σ_{2}}{({ω_{1}}{σ_{1}}+{ω_{2}}{σ_{2}})^2}}\\
&=({ω_{1}}{σ_{1}}+{ω_{2}}{σ_{2}})\sqrt{\frac{({ω_{1}}{σ_{1}}+{ω_{2}}{σ_{2}})^2-4ω_{1}ω_{2}σ_{1}σ_{2}}{({ω_{1}}{σ_{1}}+{ω_{2}}{σ_{2}})^2}}\\
&=({ω_{1}}{σ_{1}}+{ω_{2}}{σ_{2}})\sqrt{\frac{({ω_{1}}{σ_{1}}-{ω_{2}}{σ_{2}})^2}{({ω_{1}}{σ_{1}}+{ω_{2}}{σ_{2}})^2}}\\
&=|{ω_{1}}{σ_{1}}-{ω_{2}}{σ_{2}}|\\
\end{aligned}
$$
より、グラフ上の線は直線となることが分かる。
$${ρ\neq{-1}}$$の場合、グラフは弓型となるが、左端の頂点を最小分散ポートフォリオと呼ぶ(下グラフ:赤色の点)。この点におけるポートフォリオが最も効率的であるというわけではない。リスク回避的な人はこの点のポートフォリオをとるが、よりリスクを負ってでも高い収益率を求めるタイプの人はこの点より右上の領域のポートフォリオを選択する。
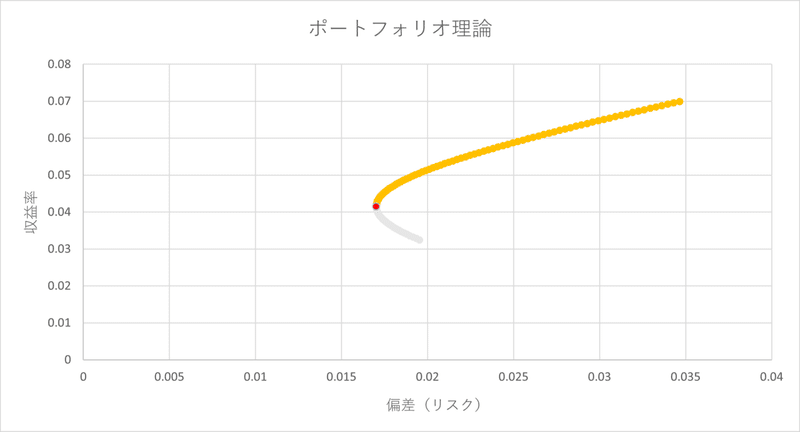
グラフ上の点のうち、最小分散ポートフォリオより右上にあるポートフォリオ(上グラフ:オレンジの線)は効率的である。この線を効率的フロンティアと呼ぶ。例えば、以下の青い点のいずれかを選択しようとする場合、同じリスクならば収益率の高い上の点を取るはずである。よって赤い点の右上のオレンジの線が効率的であると言える。
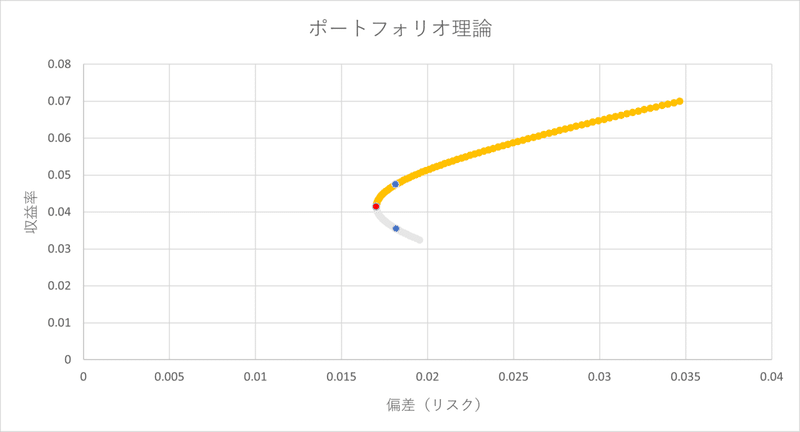
資産が二つ(有リスク資産と無リスク資産)の時のポートフォリオ理論
本章では、無リスク資産を含めたポートフォリオ理論を考える。先の文字設定を用いて計算を行うが、資産$${A_1}$$は無リスク資産とすると、収益率$${R_1}$$は常に同じで、$${R_1=μ_1}$$となる。
この時、平均収益率$${μ}$$は、先と同じで
$$
μ=E[ω_{1}R_{1}+ω_{2}R_{2}]=ω_{1}μ_{1}+ω_{2}μ_{2}
$$
偏差は、
$$
\begin{aligned}
σ&=\sqrt{Var[ω_{1}R_{1}+ω_{2}R_{2}]}\\
&=\sqrt{E[((ω_{1}R_{1}+ω_{2}R_{2})-μ)^2]}\\
&=\sqrt{E[((ω_{1}R_{1}+ω_{2}R_{2})-(ω_{1}μ_{1}+ω_{2}μ_{2}))^2]}\\
&=\sqrt{E[((ω_{1}μ_{1}+ω_{2}R_{2})-(ω_{1}μ_{1}+ω_{2}μ_{2}))^2]}\\
&=\sqrt{E[(ω_{2}R_{2}-ω_{2}μ_{2})^2]}\\
&=\sqrt{{ω_{2}}^2E[(R_{2}-μ_{2})^2]}\\
&=\sqrt{{ω_{2}}^2Var[R_{2}]}\\
&={ω_{2}}{σ_{2}}\\
\end{aligned}
$$
以上から、保有割合の変化により、収益率μと偏差(リスク)は共に線形変化することが分かる。よってグラフは、以下のように直線となる。
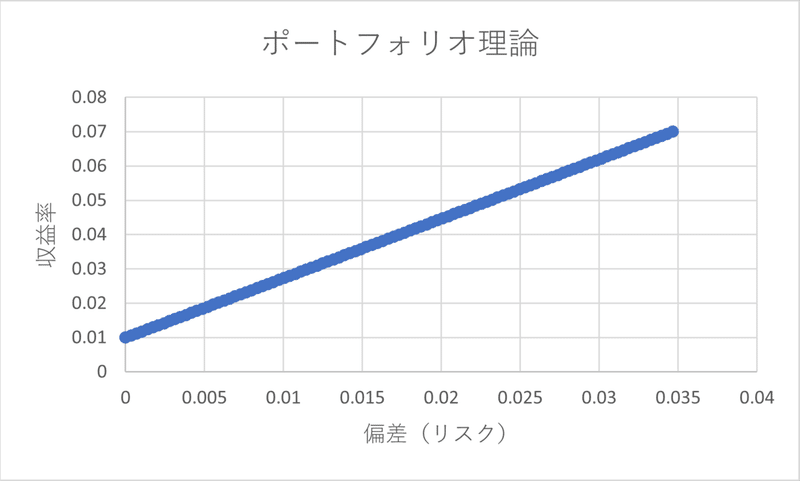
この記事が気に入ったらサポートをしてみませんか?
