画像演算

コンピュータで表現された画像に対し，加算，減算，乗算，べき乗の演算ができます！フォトショップやSNS用の写真加工のツールなど，ビットマップ画像を扱うコンピュータプログラムは，この算術演算に基づいています．
ビットマップ画像は，スクリーン上の発光画像として表現することができ，
(ピクセル）で構成される長方形の表です．それぞれのセルには，3つの基本色（赤，緑，青）の明るさを表す数値セット$${(r; g; b)}$$が格納されており，この数値でピクセルの色が決まります．$${(r, g, b)}$$の各数値は1バイト［８ビット］として格納，つまり，値の範囲は0から255$${(=2^{8}-1)}$$までの整数です．

0の値は，その色がないこと，255の値は，その色の明るさが最大であることを意味します．
例えば:
$${(0; 0; 0)}$$ - 黒ピクセル，$${(255; 255; 255)}$$ - 白ピクセル，
$${(255; 0; 0; 0)}$$ - 赤ピクセル，$${(0; 100; 0)}$$ - 暗緑色ピクセル，$${(200; 200; 0)}$$ - 黄色ピクセル．

画像に対する算術演算は，ピクセル単位で成分ごとに行われます．等しい位置にあるピクセル $${(r_1; g_1; b_1)}$$と$${(r_2; g_2; b_2)}$$の場合，それらの和は$${(r_1 +r_2; g_1 + g_2; b_1 +b_2)}$$で，積は$${([\frac{r_{1}r_{2}}{255}]; [\frac{g_{1}g_{2}}{255}]; [\frac{b_{1}b_{2}}{255}])}$$となります．
加算で255を超えれば255とし，積の定義で，括弧［］は数の整数部だけを表示します．一般に，加算は明るい点を生成し，乗算は明るさを減じます．
例えば，絵に白い背景を加えると，絵全体が白くぼんやりする．
色のついた絵に「黒い正方形」を乗ずると，正方形の「ブラックホール」ができる．
緑の三角形$${A}$$と赤の円$${B}$$とすると；

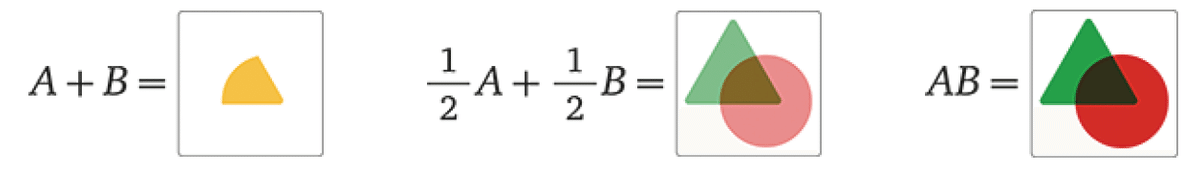
これらの演算を適用した直後の結果にはがっかりさせられる．
緑の三角形$${A}$$と赤い円$${B}$$があるとして，
$${A＋B}$$の和は交点に黄色のスライスを作る．
（訳者注：白の地の部分はすでに255なので，すでに飽和している）
もし， "ハーフイメージ "$${0.5A＋0.5B}$$を作ると，三角形と円の形は変わらないが，色は変化する：図形の交叉は暗い影になり，残り部分は明るくなる．積$${AB}$$では，図形の交叉が暗くなり，他の部分は元の色を保つ．
しかし，単色灰色マスク（つまり黒から白のある階調の画像）を使えば，実用的な問題の大部分は「算術的」に解くことができる．
黒と白のマスク$${M_A}$$ と$${M_B}$$ を考えてみよう．$${A}$$ と $${B}$$ にマスクを乗ずると，物体そのものが白くなり，白い背景が黒くなる．
さらに2つのマスク，$${\overline{M_{A}}}$$と$${\overline{M_{B}}}$$はその「反転」であり，黒と白が入れ替わる．

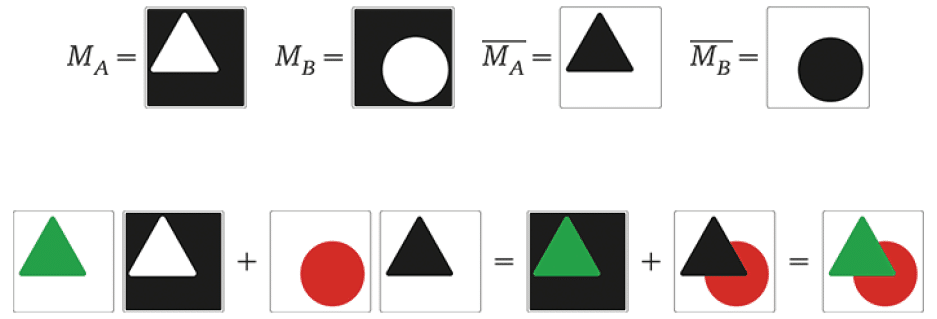
画像Aにマスク$${M_{A}}$$を乗ずると，黒い背景に三角形の画像ができ，画像Bにマスク$${\overline{M_{A}}}$$を乗ずると，黒い三角形が丸で切り取られる．
結局， 画像$${AM_A + B \overline{M_{A}}}$$は，赤い円$${B}$$上に緑の三角形$${A}$$を重ねたものになる．同様に，$${BM_B + A \overline{M_{B}}}$$ は，緑の三角形上の赤い円を重ね合わせたものになる．
上記のマスクは白黒だったが，"真の "灰色マスクも使われる．たとえば，重ね合わせた画像を半透明にするために使うことができる．黒と白のマスクの直線的な組み合わせである2つの灰色マスクは，円に三角形を重ねた半透明の重ね合わせを作り出す．$${A(0.7M_{A} +0.3 \overline{M_{B}}) + B(0.7 \overline{M_{A}} +0.3M_{B})}$$

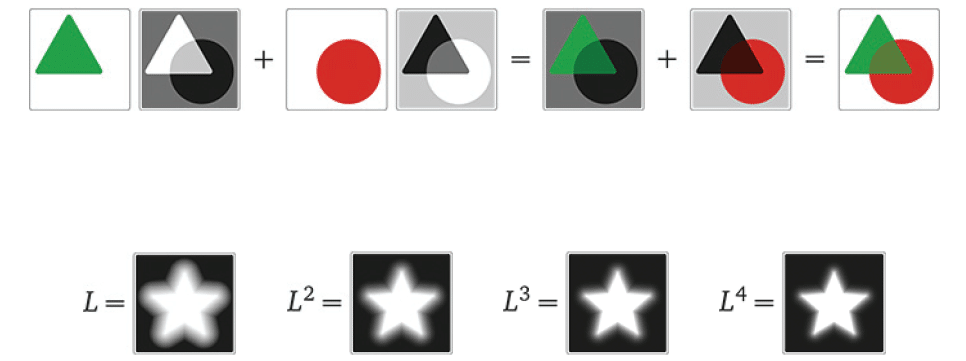
また，モノクロ写真をシャープにする「べき乗」など，1枚の画像だけで作業するときに便利なツールもあります．
基本的な操作は，個々のピクセルに対する処理という最も単純なモデルで考えたのですが，周囲のピクセルの色を考慮してピクセルの色を変更するツールも使用されています．例えば，色の平均化は写真をぼかす効果を与えます．

応用：画像処理
数学：算術演算，ベクトル
『数学構成要素』p.126-127より