
結晶群とその一般化(1)
空間群の発見
群拡大理論による基礎づけ
群の一般化,特性の対称性
対称性.群
結晶空間
フェドロフ結晶空間群
■ 対称性と点群
群
集合$${G=\{a, b, c, \cdots \}}$$が群と呼ばれるのは,次の公理を満たす場合である:
0) $${a, b \in G}$$, $${a \circ b \in G }$$ ⇐ 二項演算が定義される
1) $${\left( a \circ b \right) \circ c=a \circ \left( b \circ c \right)}$$ ⇐結合律
2) $${a \circ e=e \circ a=a}$$ ⇐単位元$${e}$$の存在,for$${ \forall a \in G}$$
3) $${a \circ x=x \circ a=e}$$ ⇐$${a}$$の逆元$${x=a^{-1}}$$の存在
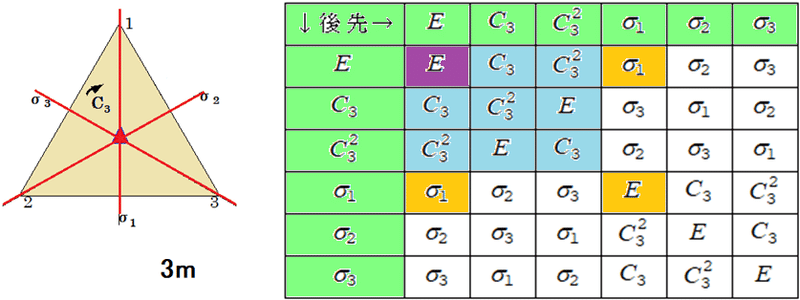
◆ 群の乗積表(3mの例)で群の公理を確認ください.
■ 群の例
結晶空間の対称操作の集合の作る群を考えよう:
結晶空間=周期的な空間=単位胞によりデジタル化された空間
・結晶空間で1点の特異点(不動点)をもつ対称操作の組み合わせ結晶点群
・不動点はない結晶空間の対称操作の組み合わせ 結晶空間群
結晶空間(デジタル化された空間)は無限に広がる格子のイメージ:
格子点はすべて同値と見做すならば,結晶空間群は結晶点群に還元できる.
⇒結晶空間群は,並進群を核(法として)とする準同型写像で結晶点群と同型
無限に経過する時間を,時計の文字盤(12時間)に閉じ込めるようなもので,無限に繰り返す周期的な結晶空間を単位胞のなかに閉じ込める.


■ 2次元で演習:
2次元平面を並進だけでタイル張りできる平行凸多辺形タイルは,
平行4辺形(4種),平行6辺形(4種)である.
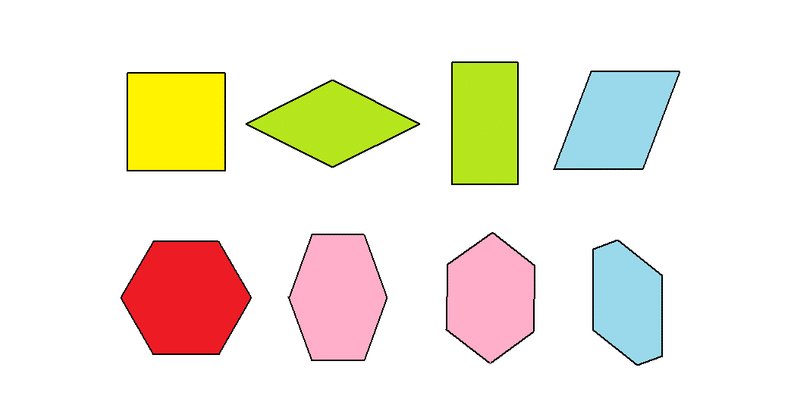
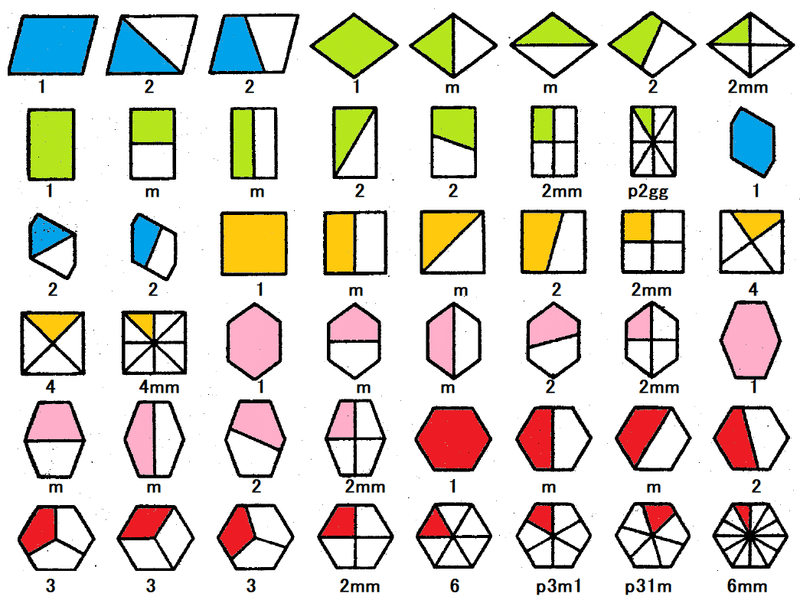
8つの各平行多辺形を等価な部分に分割すると,図のように40種類の様式があり,対称性の同じものをまとめ整理すると,共型平面群13種類(映進操作を含まないもの)が数え上げられる.点群(並進を含まないもの)としては10種である.ただし,上図の分割様式中に非共型平面群1種類,p2ggがすでに出現している.しかし,共型群(13種類)を求めて,それから,非共型群(4種類)を導くのが王道である.2次元空間群(平面群)は計17種類ある.
詳細は以下の項目参照;
■ 2次元結晶空間群のまとめ

■ 3次元結晶空間群
A.M.シェンフリーズ(1853-1928,フランクフルト大,数学)
E.S.フェドロフ(1853-1919,ぺテルスブルグ大,鉱物学)
W.バーロー(1845-1895,ロンドンの実業家)
この3人は,1890-1895の間に互いに独立にそれぞれの仕事を完成させた.

周期的な3次元空間を充填できる平行多面体は,フェドロフ平行多面体と言い5種類ある.2次元の場合と同様にそれぞれを等価な部分に分割して,対称性の異なるものだけ数え上げると,3次元結晶空間の場合は230種類があるが,そのうちの共型なもの73種類が得られる.さらにそれらから非共型なもの157種類の導出は2次元の場合と同様である.
結晶空間群の発見は,その20年後に実用化される運命であったX線結晶構造解析への準備となった.
1895,W.C.レントゲンがX線を発見.1912,M. vonラウエが結晶によるX線の回折を観測.1913以降,ブラッグ父子によりダイヤモンドなどの結晶構造解析が行われる.
この記事が気に入ったらサポートをしてみませんか?
