Pythonで宇宙を楽しもう Vol.1 プログラミングで微分方程式を解く

新マガジン 「Python で宇宙を楽しもう」をはじめました！
こちらは記念すべき第一回です。

それではさっそくみなさんのパソコンで宇宙を再現していきましょう！
と、言いたいところですが...そのためには準備体操が必要です。

最初の数回ではその手始めとして、簡単な問題を解き、Python の書き方を学びながら勧めていきましょう。

今日は、

「vol.1 プログラミングで微分方程式を解く」

です。

微分方程式とは？

wikipediaによると、微分方程式とは

未知関数とその導関数の関係式として書かれている関数方程式

らしいです。（https://ja.wikipedia.org/wiki/微分方程式）

うん、よくわかりませんね。具体的に考えてみましょう。

ある関数 $${y = f(x)}$$ を考えます。これは、$${y}$$ が $${x}$$ によって決定されるということを表しています。ここで、$${y}$$について以下の関係が与えられました、

$${\frac{dy}{dx} = -2xy}$$

これは、$${y}$$ の微分が $${-2xy}$$ で与えられるということであり、この微分方程式を解くということは「$${y}$$ の微分が $${-2xy}$$ で与えられる」という条件から $${y}$$ を導く、ということになります。

この微分方程式は解析的に解くことができて、$${ y = Ce^{-x^{2}} }$$ （$${C}$$は定数）となります。

では、この微分方程式を数値的に解いてみましょう。

オイラー法

オイラー法は微分方程式の数値的解法の基礎ともいえる手法です。この手法を理解するためには、先に上げた微分方程式を次のように変形するとわかりやすいです。

$${dy = -2xy \times dx}$$

ある点 $${x_{i}, y_{i}}$$からx軸方向に$${dx}$$ だけ進んだ先の関数の値は、与えられた微分方程式から上の式を用いて、$${y_{i} + dy}$$ と求められます。

この手法を用いることで関数の形を数値的に求めることができます。また、その進む幅$${dx}$$が小さいほど、精度が良くなることも下の図のように考えればイメージできるでしょう。

 中点法（コーシー法）

中点法も、その大まかな手法は オイラー法と変わりません。異なるのはその名の通り、ステップサイズを一気に進むのではなく、中点まで進んだ位置における傾きを求めて、その傾きを用いてステップサイズ先の点における関数の値を推定するというところです。

同じステップサイズでも、オイラー法の倍細かく計算しているので精度が良くなるというわけですね。

Pythonで実装する

まずは、計算に必要なパッケージをインポートします。

### Typical numerical calculation

## header
import numpy as np
import math 
import matplotlib.pyplot as plt
## 

オイラー法を実装します。

大まかなな流れは、

・与えられた微分方程式を関数として定義

# differential of y
def dif(x, y):
   dydx = -2.0 * y * x
   return dydx

・初期条件（計算をスタートする値）、ステップサイズ、計算の繰り返し回数を決める。

# Initial condition
x0 = 0
y0 = 1

# stepsize
dx = 0.1

# number of iteration
n = 1e2

・ステップサイズごとに傾きを計算し、yに足し合わせていくことを繰り返す。
　（#array for plot の辺りと最後の一文はプロットのためのコードです）

x = x0 
y = y0

# array for plot
Xe = []
Ye = []

for i in range(int(n)):
   Xe.append(x)
   Ye.append(y)
   # calculate next step
   x1 = x + dx
   y1 = y + dx * dif(x,y)

   x = x1
   y = y1

plt.plot(Xe, Ye, label='Euler', linewidth = 1.0)

同様にコーシー法と解析解をプロットする

# analytical
# plot range
xmin = 0
xmax = 10

# step number
N = 1000

# make array
p = np.linspace(xmin, xmax, N)
q = np.exp(-p**2.0)

plt.plot(p, q, label='analytical', linewidth = 1.0)

################
## Cauthy method
################
# Initial condition
x0 = 0
y0 = 1

# stepsize
dx = 0.1

# number of iteration
n = 1e2

x = x0 
y = y0

# array for plot
Xc = []
Yc = []

for i in range(int(n)):
   Xc.append(x)
   Yc.append(y)

   x05 = x + 0.5*dx
   y05 = y + 0.5*dif(x, y)*dx

   x1 = x + dx
   y1 = y + dif(x05, y05)*dx

   x = x1
   y = y1

print(Xc, Yc)
plt.plot(Xc, Yc, label='Cauchy', linewidth = 1.0)

plt.xlim(0, 2)
plt.ylim(1e-2, 1.2)
plt.yscale('log')
plt.legend()
plt.title('Typical numerical solution')
#plt.show()
plt.savefig('./plot/01/numerical.png')

解析解との比較

上記のコードを用いて、$${\frac{dy}{dx} = -2xy}$$ を解き、実際の解析解と比べた結果がこちらになります。

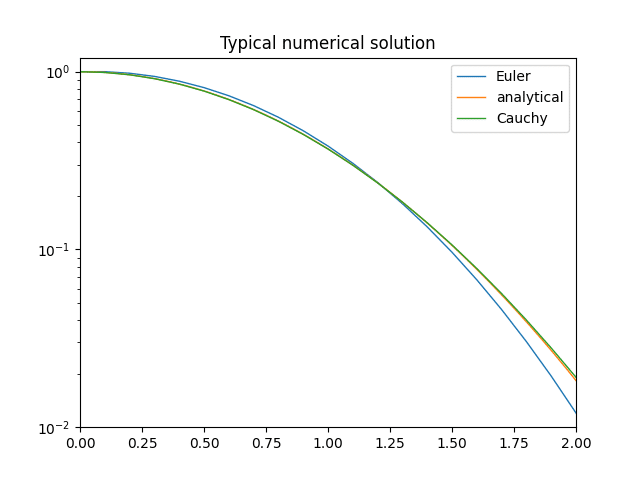
一見、ざっくりとした手法のようですが、どちらも解析解にある程度近い概形を再現できていますね。また、中点法のほうが解析解によく一致していることが見て取れます。

今回は、解析的に解ける微分方程式を用いましたが、実際には解析的には解けない関数がうじゃうじゃ存在しており、そういったものと対峙したときに頼りになるのが今回学んだ「オイラー法」や「中点法（コーシー法）」といった手法というわけです。

他にも、さらに高い精度で求めたいときは「ルンゲクッタ法」という中点法よりもさらにステップサイズのなかで細かに傾きを求める手法があります。興味がある方はぜひ調べてみてください。今回のマガジンではそこまでの精度を求めた計算は行わないので、ここでは割愛します。

少し数学が入ってきて、うーん、と唸ってしまったかたもいるかも知れません。気になることがあればぜひコメントで質問してください。

次回は、関数の零点を求める手法 ニュートン-ラフソン法 についてまとめます。

最後まで読んでいただき、ありがとうございました！

本noteは以下の資料を参考にしています。
興味のある方はお近くの本屋さんや図書館で探してみてください！

パソコンで宇宙物理学―計算宇宙物理学入門

本noteでは、この本で BASIC と呼ばれるプログラミング言語で書かれたコードを Python によるプログラミングによって焼き直しています。

コード全文は以下のとおりです。

### Typical numerical calculation

## header
import numpy as np
import math 
import matplotlib.pyplot as plt
## 

###############
## Euler method
###############

# differential of y
def dif(x, y):
   dydx = -2.0 * y * x
   return dydx

# Initial condition
x0 = 0
y0 = 1

# stepsize
dx = 0.1

# number of iteration
n = 1e2

x = x0 
y = y0

# array for plot
Xe = []
Ye = []

for i in range(int(n)):
   Xe.append(x)
   Ye.append(y)
   # calculate next step
   x1 = x + dx
   y1 = y + dx * dif(x,y)

   x = x1
   y = y1

plt.plot(Xe, Ye, label='Euler', linewidth = 1.0)


# analytical
# plot range
xmin = 0
xmax = 10

# step number
N = 1000

# make array
p = np.linspace(xmin, xmax, N)
q = np.exp(-p**2.0)

plt.plot(p, q, label='analytical', linewidth = 1.0)

################
## Cauthy method
################
# Initial condition
x0 = 0
y0 = 1

# stepsize
dx = 0.1

# number of iteration
n = 1e2

x = x0 
y = y0

# array for plot
Xc = []
Yc = []

for i in range(int(n)):
   Xc.append(x)
   Yc.append(y)

   x05 = x + 0.5*dx
   y05 = y + 0.5*dif(x, y)*dx

   x1 = x + dx
   y1 = y + dif(x05, y05)*dx

   x = x1
   y = y1

print(Xc, Yc)
plt.plot(Xc, Yc, label='Cauchy', linewidth = 1.0)

plt.xlim(0, 2)
plt.ylim(1e-2, 1.2)
plt.yscale('log')
plt.legend()
plt.title('Typical numerical solution')
#plt.show()
plt.savefig('./plot/01/numerical.png')

（その際は、引用元としてこちらのnoteと上記の本を書いていただけますよう、お願いします。）

☆================================
さあ星空を見上げよう
プロフィール
・天文学を学ぶ大学三年生（もうすぐ四年生）

すきなもの
・宇宙に関連するもの
・BUMP OF CHICKEN さん（ミュージシャン）
・SEKAI NO OWARI さん（ミュージシャン）
・伊坂幸太郎 さん（小説家）
・マンドリン音楽

質問・コメント大募集中！
「こんな宇宙の話を聞いてみたい！」
「天文学でよく聞く 〇〇 って何？」
==================================