【探究】sin15°
視点を変えながら,$${\sin15°}$$を考えよう。
後半の3つは直角三角形の定規があると楽しめる解法です。
➀ 数学Ⅰ(余弦定理)
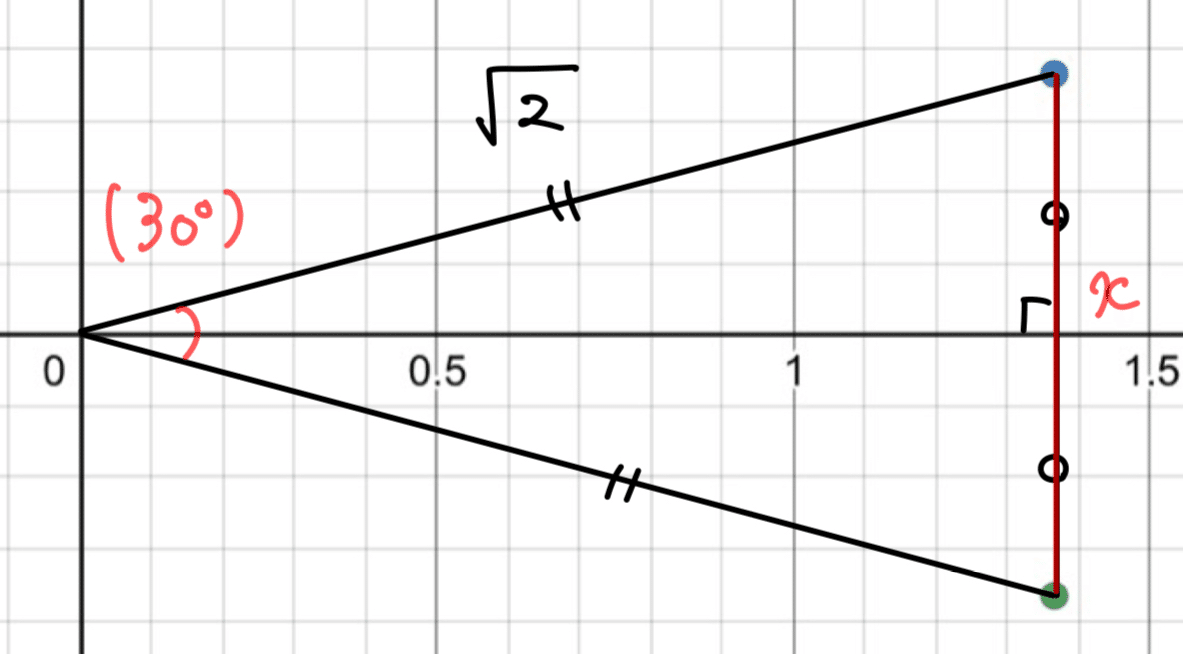
頂角が30°の二等辺三角形を考える。2辺の長さを$${\sqrt{2}}$$,頂角の対辺の長さを$${x}$$とすると,余弦定理より
$${x^{2}=(\sqrt{2})^{2}+(\sqrt{2})^{2}-2\cdot\sqrt{2}\cdot\sqrt{2}\cdot\cos30°=4-2\sqrt{3}=(\sqrt{3}-1)^{2}}$$
$${x>0}$$なので,$${x=\sqrt{3}-1}$$
ここで,頂角から底辺に垂線を下ろす。
直角三角形の15°の対辺の長さが$${\frac{x}{2}=\frac{\sqrt{3}-1}{2}}$$なので
$${\sin15°=\frac{\sqrt{3}-1}{2\sqrt{2}}=\frac{\sqrt{6}-\sqrt{2}}{4}}$$
② 数学Ⅱ(加法定理)
$${\sin(\alpha-\beta)=\sin\alpha\cos\beta -\cos\alpha\sin\beta}$$ より
$${\sin(45°-30°)=\sin45°\cos30°-\cos45°\sin30°}$$
$${\sin15°=\frac{\sqrt{2}}{2}\cdot\frac{\sqrt{3}}{2} -\frac{\sqrt{2}}{2}\cdot\frac{1}{2}=\frac{\sqrt{6}-\sqrt{2}}{4}}$$
③ 数学Ⅱ(2倍角の公式)
$${\sin^{2}\theta=\frac{1}{2}(1-\cos 2\theta)}$$ より
$${\sin^{2}15°=\frac{1}{2}(1-\cos 30°)=\frac{1}{2}(1-\frac{\sqrt{3}}{2})=\frac{2-\sqrt{3}}{4}}$$
$${=\frac{4-2\sqrt{3}}{8}=\frac{(\sqrt{3}-1)^{2}}{8}}$$
$${\sin15°=\frac{\sqrt{3}-1}{\sqrt{8}}=\frac{\sqrt{6}-\sqrt{2}}{4}}$$
④ 中学数学(三平方の定理)
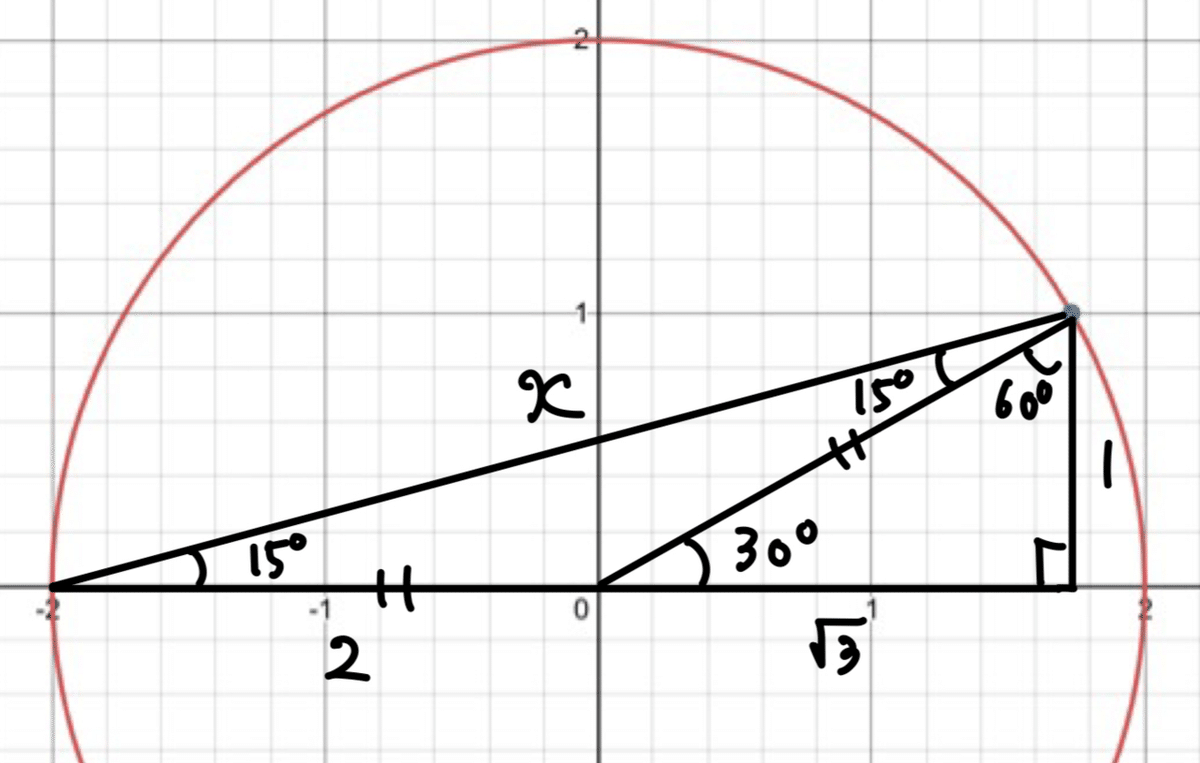
図で,三平方の定理より
$${x^{2}=1^{2}+(2+\sqrt{3})^{2}=8+4\sqrt{3}=8+2\sqrt{12}=(\sqrt{6}+\sqrt{2})^{2}}$$
$${x>0}$$なので,$${x=\sqrt{6}+\sqrt{2}}$$
よって,$${\sin15°=\frac{1}{x}=\frac{1}{\sqrt{6}+\sqrt{2}}=\frac{\sqrt{6}-\sqrt{2}}{4}}$$
⑤ 数学ⅠA(トレミーの定理~正弦定理)
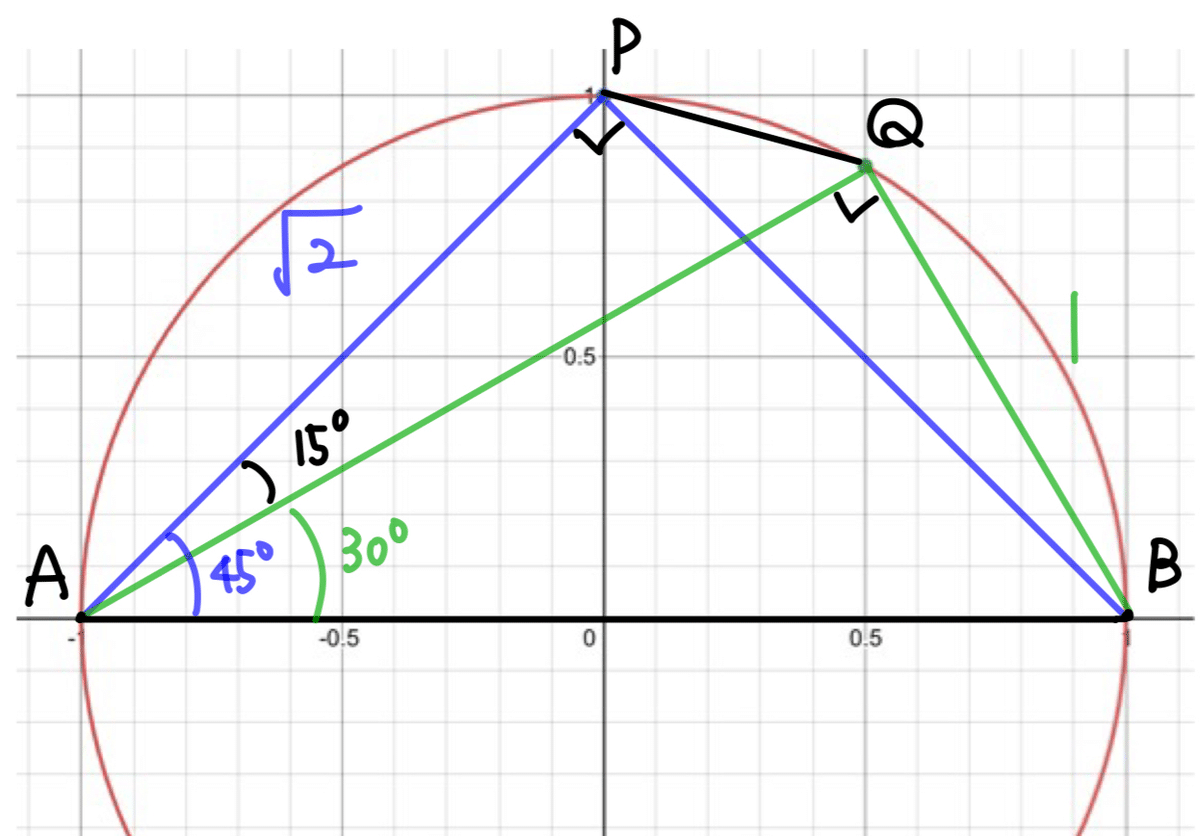
斜辺の長さが2となる直角三角形を考える。
斜辺ABに対して,直角となる2点P,Qが同一円周上にあるので,PQ$${=x}$$として,トレミーの定理より
$${1\cdot\sqrt{2}+2x=\sqrt{2}\cdot\sqrt{3}}$$
$${x=\frac{\sqrt{6}-\sqrt{2}}{2}}$$
△APQで,正弦定理より
$${\frac{x}{\sin15°}=2}$$
$${\sin15°=\frac{x}{2}=\frac{\sqrt{6}-\sqrt{2}}{4}}$$
⑥ 数学Ⅰ(正弦定理)
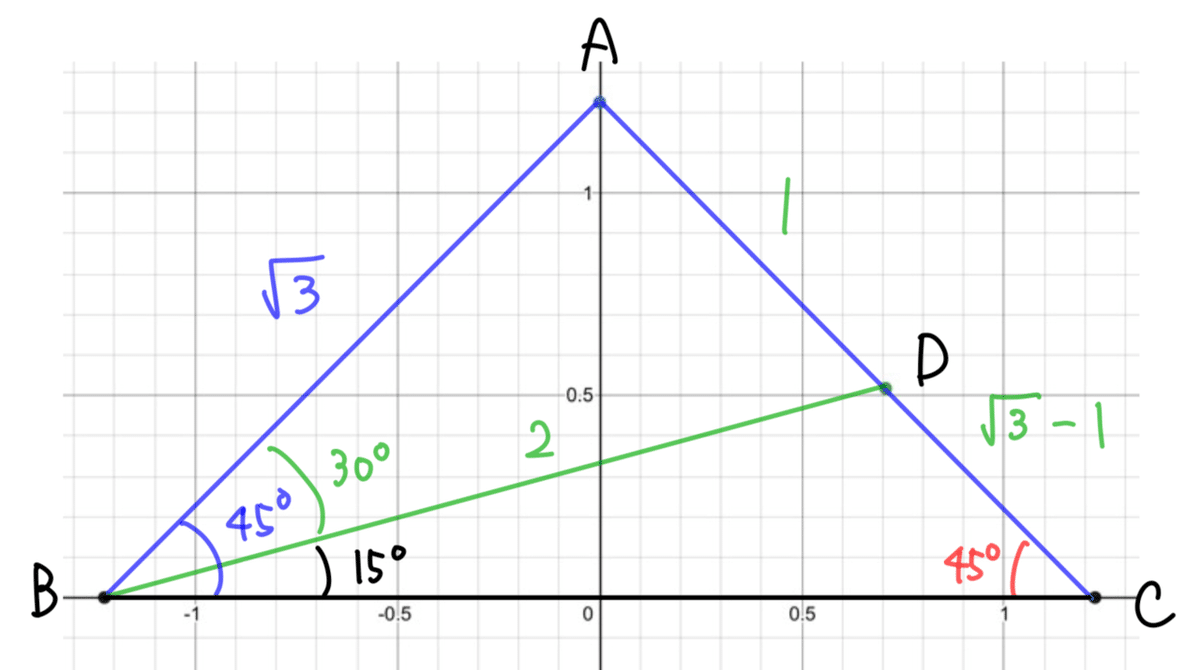
△BCDで,正弦定理より
$${\frac{\sqrt{3}-1}{\sin15°}=\frac{2}{\sin45°}}$$
$${\sin15°=(\sqrt{3}-1)\cdot\sin45°\cdot\frac{1}{2}=\frac{\sqrt{6}-\sqrt{2}}{4}}$$
この記事が気に入ったらサポートをしてみませんか?
