LLMファインチューニングのためのNLPと深層学習入門 #6 マルチヘッドアテンション

Sakusakumura

今回は、CVMLエキスパートガイドの『マルチヘッドアテンション』を勉強していきます。

1. 概要

マルチヘッドアテンションとは、複数のアテンションヘッドを並列実行して、系列中の各トークン表現の変換を行うブロック部品です。
マルチヘッドアテンションは、Transformerで提案された、複数の視点（これが「アテンションヘッド」）から同時にデータを理解しようと試みる仕組みです。
端的に言うと「並列型アテンション」となります。

より具体的には、図１のようになります。

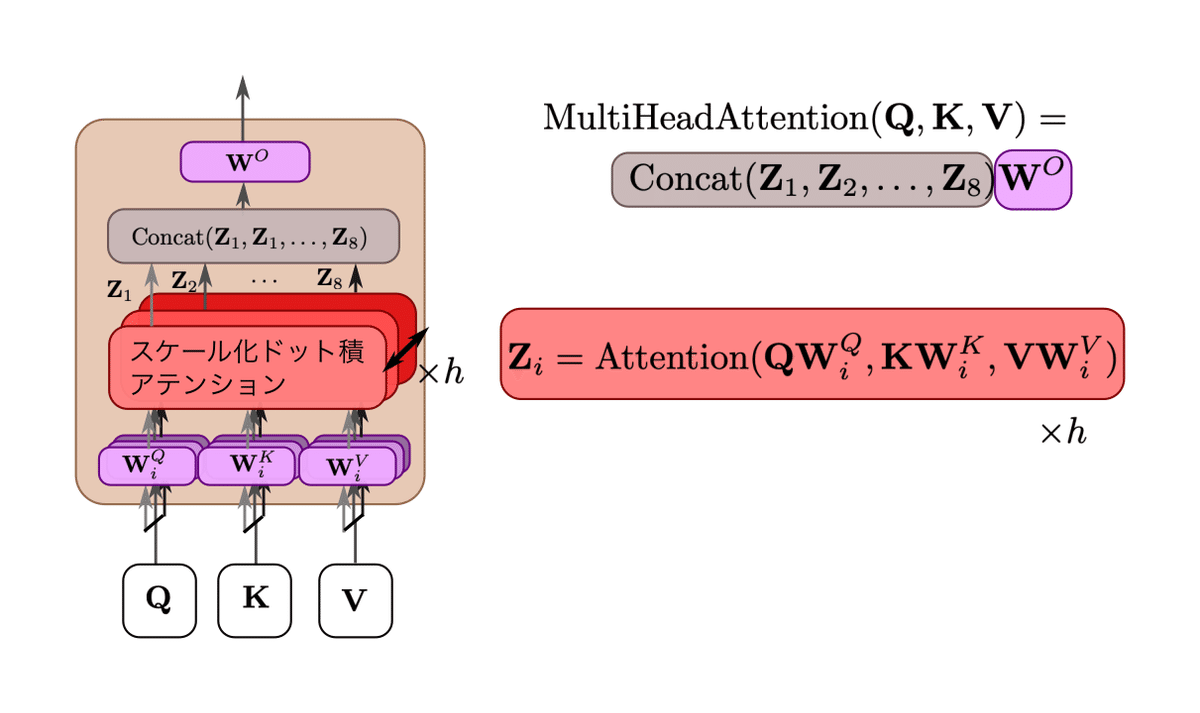
図1. マルチヘッドアテンション(Multi-head Attention) [Transformerの主部品]
CVMLエキスパートガイドより引用

マルチヘッドアテンションは、入力のシーケンス長n × トークン表現次元 $${d_{model}}$$のサイズで構成される行列である$${Q}$$(Query), $${K}$$(Key), $${V}$$(Value)を、h個の並列したヘッドで異なる処理を行った結果を$${Z_i}$$のように１つに結合する処理です。

2. マルチヘッドアテンションの利点

マルチヘッドアテンションでは「ソース・ターゲット系列間のグローバルな関係コンテキストを加味できる」うえに、系列中の全トークン表現の一括変換ができます。

簡単な演算（ドット積アテンションの並列化）ながら高精度な系列変換をTransformerが実現できるのは、このマルチヘッドアテンションを自己回帰的にEncoder側で6回、Decoder側で12回使用するスタックされた設計のおかげです。

系列全体の「一括アテンション処理」

従来のseq2seq with attention時代では、以下の２つの処理により、ローカル処理かつフレーム単位の自己回帰予測を行っていました。

  • seq2seq with attentionのシングルアテンション

  • RNN または畳み込み層によるフレーム間遷移

これに対し、Transformerでは窓サイズTのマルチヘッドアテンションを用い「T個のトークン幅」での系列内の各トークン表現を一気に変換するようになりました。
また、一度に全てのトークン表現を変換するので「系列全体の長期依存コンテキスト」を加味できるようになり、系列対系列変換性能も向上しました。

ここで、窓サイズとは、一度に扱う連続したトークン（またはデータポイント）の数を指します。
一般に、自然言語処理や時間系列解析では、一部のデータを一度に扱う際に「窓」という概念が用いられます。
この窓の大きさ、つまり「窓サイズ」は一度に処理されるデータの量を決定します。

※「T個のトークン幅」と表現しているのは、Transformerにおけるマルチヘッドアテンションの窓サイズが、理論上は入力に応じて任意に変化するからです。
つまりTは単なるプレースホルダーとして用いられています。

3. マルチヘッドアテンションの詳細

図1（再掲）. マルチヘッドアテンション(Multi-head Attention) [Transformerの主部品]
CVMLエキスパートガイドより引用

マルチヘッドアテンションは、並列にアテンションを実行するためのTransformer向けブロックです。
QKV入力方式のスケール化ドット積アテンションを、h個並列に実施した後、最後にh個の表現を1つに結合して、全体を全結合層$${W^O}}$$で線形変換した結果を最終出力とします。

  • 論文 "Attention is All You Need"（Vaswani et al., 2017）における基本的なTransformerモデルの設定では、h=8でした。
    この数値はハイパーパラメータなので、問題の性質やデータセットの大きさにより調整可能です。

また、各ヘッドの「QKV低次元射影変換＋QKVアテンション変換」には、それぞれ異なる変換が学習されています。
つまり、入力系列をQKV方式の潜在表現に変換する処理と、マルチヘッドによるQKVアテンションの計算結果の合成にニューラルネットワークが関与するということです。
（後述しますが、QKVアテンションの計算にはニューラルネットワークは関与しません）

これにより、それまで主流だったシングルヘッドアテンションよりも表現力が高くなり、高精度な変換をシンプルな並列計算だけで学習できるようになりました。

「(1)並列計算」かつ「(2)行列演算（ドット積）中心」で設計されているので、計算機的に非常に有利です。

4. マルチヘッドアテンションの処理手順

マルチヘッドアテンションでは、入力の「トークン表現の系列」の変換処理を、以下の３つの手順でh個のアテンションヘッドで並列に行います。
ここで、"Attention is all you need"ではh=8だったので、h=8として解説します。

  1. 前処理：トークン表現の次元削減

    • 入力のQ, K, V を構成する入力ベクトル$${x}$$を$${d_k = d_v = d_{model} / h= 64}$$の低次元ベクトルへと、ヘッドごとに個別の全結合層$${W^Q_i, W^K_i, W^V_i}$$（ここでヘッドはi番目としています）を用いて射影

    • 入力は前の層から来るため、埋め込み層ではありません。

  2. 本処理：h個のアテンションを並列実行

    1. 低次元に射影された$${QW^Q_i, KW^K_i, VW^V_i}$$を入力に、8個のスケール化ドット積アテンション（後述のQKV方式アテンション）を実行します。

    2. 結果として、8個のアテンション重みづけされたトークン表現$${Z_1, Z_2, …, Z_8}$$が得られます。
      ここで、$${Z}$$は行列です。

  3. 後処理：並列処理結果の結合と最後の線形変換

    1. $${Z_i}$$内の各トークン表現を、１つのベクトルにそれぞれ結合します。
      結果として、$${8 \cdot d_v = 512}$$次元ベクトル表現になります。

    2. 結合したものを、全結合層$${W^O}$$で変換します。
      これにより、並列アテンション処理中の$${h \cdot d_v}$$次元から、もとの$${d_{model}}$$次元に戻った最終的なトークン表現出力を得ます。

5. QKV方式アテンション

各ヘッドで使用される「スケール化ドット積アテンション」は、QKV方式アテンションです。
QKV方式アテンションは、Transformerモデルのセルフアテンション（自己注意）メカニズムにおける重要な要素で、Q, K, VはそれぞれQuery, Key, Valueを指します。

これらの項目は以下のように役割を持ちます。

  • Query（クエリ）：
    アテンションメカニズムがどの情報に焦点を当てるべきかを示すものです。
    現在のトークンが他のトークンとどの関連性を持つかを判断するために使用されます。
    検索キーワードのようなものです。

  • Key（キー）：
    キーは、そのトークンが持つ情報の特徴を表します。
    各トークンはキーとして自身の情報の特性や特徴を提供し、クエリとの関連性が計算されます。

  • Value（バリュー）：
    そのトークンが持つ情報そのものを表します。

そして、次の式で各入力トークンの情報を、その他のトークンとの関連性に基づいて重み付けした行列が得られます。

$$
\mathrm{
Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}}) * V
}
$$

QとKはそれぞれクエリとキーの集合を表現した行列で、各行は特定のトークンのクエリまたはキーを表します。
Qの行列形状は$${n \times d_k}$$で、Kの形状は$${m \times d_k}$$です。
（nとmはそれぞれクエリとキーのトークン数、d_kはクエリとキーの次元数）
ここで、$${Attention(Q, K, V)}$$の出力、$${Q, K, V}$$は全て行列であることに注意してください。

6. アテンションの重みを求めてみる

1. 変数定義

ここで、Qのトークン数をn, Kのトークン数をmとして、

$$
n = 2 \\
m = 3 \\
d_k = 2
$$

とします。
行列の数値は適当に決めます。
なので、数値の意味はありません。
処理の流れ、計算結果がどのような意味を持つのかを理解するのが目的です。
Qの行列形状は$${n \times d_k}$$、Kの形状は$${m \times d_k}$$なので

$$
Q=\begin{bmatrix}
1 & 2 \\
3 & 4
\end{bmatrix} 
K=\begin{bmatrix}
4 & 5 \\
6 & 7 \\
8 & 9
\end{bmatrix} 
$$

>>> Q = np.array([[1, 2], [3, 4]])
>>> Q
array([[1, 2],
       [3, 4]])
>>> K = np.array([[4, 5],
...               [6, 7],
...               [8, 9]])
>>> K
array([[4, 5],
       [6, 7],
       [8, 9]])

2. クエリとキーの関連度計算

まず、$${Q}$$と$${K^T}$$のドット積$${QK^T}$$を求めると、次の行列が得られます。

$$
QK^T= \begin{bmatrix}
14 & 20 & 26 \\
38 & 56 & 74
\end{bmatrix} 
$$

>>> dot_product = np.dot(Q, K.T)
>>> dot_product
array([[14, 20, 26],
       [32, 46, 60]])

この行列は全てのクエリとキーの間の関連性を表しています。
i行j列目の要素は、i番目のクエリトークンとj番目のキートークンの間の関連性を表します。
このようにして、全てのクエリトークンについて、全てのキートークンとの関連性を一度に計算することができます。

3. 値のスケーリング

その後、この行列に$${\frac{1}{\sqrt{d_k}}}$$をかけることでドット積が次元数に依存する影響を抑制します。
具体的には、この後説明するsoftmax関数で行列の全ての成分の和を１にして確率分布として解釈できるようにするのですが、次元数が増えるとドット積の結果が非常に大きくなる可能性があります。
これはsoftmax関数が指数関数を使用しているためで、そのまま（大きい値を）softmax関数に入力してしまうと、出力が急速に０または１に近づいてしまう問題があります。
そこで、$${\frac{1}{\sqrt{d_k}}}$$でスケーリングすることにより、この問題に対処します。

>>> d_k = Q.shape[1]
>>> d_k
2

>>> sqrt_d_k = np.sqrt(d_k)
>>> sqrt_d_k
1.4142135623730951

>>> scaled_dot_product = dot_product / sqrt_d_k
>>> scaled_dot_product
array([[ 9.89949494, 14.14213562, 18.38477631],
       [22.627417  , 32.52691193, 42.42640687]])

簡単にすると次のようになります。

$$
{scaled\_dot\_product} = \begin{bmatrix}
9.9 & 14.1 & 18.4 \\
22.6 & 32.5 & 42.4
\end{bmatrix} 
$$

4. 正規化

ステップ３で得た、スケール済みの行列をsoftmax関数に通すことで正規化を行います。
softmax関数は以下の通りです。

$$
softmax(x_i) = \frac{e^{x_i}}{\sum_j{e^{x_j}}}
$$

ここで、$${x_i}$$はベクトル$${x}$$のi番目の成分です。
$${\sum_j{e^{x_j}}$$はベクトル$${x}$$の全ての成分を$${e}$$の累乗として計算し、その結果をすべて加算したものです。

この関数によって全ての成分の和が１になり、確率分布として解釈することができるようになります。
そして、この結果こそが、アテンション重みです。
i行j列目の要素は、i番目のクエリとj番目のキーの間のアテンション重みを表します。

>>> def softmax(x):
...   if (x.ndim == 1):
...     x = x[None,:]    # ベクトル形状なら行列形状に変換
...   # テンソル（x：行列）、軸（axis=1： 列の横方向に計算）
...   return np.exp(x) / np.sum(np.exp(x), axis=1, keepdims=True)
...
>>> softmax_output = softmax(scaled_dot_product)
>>> softmax_output
array([[2.03518785e-04, 1.41631528e-02, 9.85633328e-01],
       [2.51991649e-09, 5.01975098e-05, 9.99949800e-01]])

（softmaxの関数はitmediaさまの記事『［活性化関数］ソフトマックス関数（Softmax function）とは？』より流用させていただきました）

簡単にすると次のようになります。

$$
{scaled\_dot\_product} = \begin{bmatrix}
0 & 0 & 1 \\
0 & 0 & 1
\end{bmatrix} 
$$

5. アテンション重みの適用

最後に、softmax の出力に、各キーに対応するバリュー（Value）を掛けます。
バリュー行列 V を以下のように設定します。

$$
K=\begin{bmatrix}
10 & 11 & 12 \\
13 & 14 & 15 \\
16 & 17 & 18
\end{bmatrix} 
$$

softmax の出力と新しい V を掛けると次のようになります

>>> V = np.array([[10, 11, 12], [13, 14, 15], [16, 17, 18]])
>>> V
array([[10, 11, 12],
       [13, 14, 15],
       [16, 17, 18]])

>>> attention = np.dot(softmax_output, V)
>>> attention
array([[15.95628943, 16.95628943, 17.95628943],
       [15.99984939, 16.99984939, 17.99984939]])

簡単にすると次のようになります。

$$
{scaled\_dot\_product} = \begin{bmatrix}
16 & 17 & 18 \\
16 & 17 & 18
\end{bmatrix} 
$$

ここで、i行j列目の要素は、i番目のクエリにおけるj番目のキーのアテンション重みづけされた情報を表しています。

7. Transformerにおけるマルチヘッドアテンション

Transformer内の各マルチヘッドアテンションは、入力のQKVがそれぞれどこから生成されたものかを切り替えることで、自己アテンションなのか、相互アテンションなのかを変化させることができます。

7.1 自己アテンションと相互アテンションの違い

自己アテンションと相互アテンションは、Transformer登場以前から存在する考え方です。
これらはアテンションを系列対系列変換で用いる際に、次のような違いで分類されます。

  1. 自己アテンション（self-attention）
    系列内での各トークン表現間のアテンション

  2. 相互アテンション（cross-attention）
    系列間での各トークン表現間のアテンション

図2. 自己アテンションと相互アテンションの比較
CVMLエキスパートガイドより

前回学習したseq2seq with attentionでは、系列間でのトークン表現の関連度を学習します。
そのため、相互アテンション（系列間アテンション）です。

Transformerが自己アテンションの良さを前面に押し出して人気モデルとなったことから、自己アテンションと相互アテンションという２つの呼び方が主流になりました。

8. 「自己 or 相互」でTransformerの各アテンションを復習

以下の図３は、Transformerの全体構成図です。
構成部品の多くを省略してあります。

図3. Transformerの簡略図 (自己アテンション or 相互アテンション の違いに注目)CVMLエキスパートガイドより

この図では、各マルチヘッドアテンションにおける、以下２点の違いが分かりやすく確認できます。

  1. 入力のQ, K, Vのそれぞれが「X(入力系列)から来ている 」か「Y(出力系列)から来ている」か。

  2. 「自己アテンション」か「相互アテンション」か

各アテンションの違い: EncoderとDecoderの構成について

  • Transformer-Encoderブロック（×６回）

    1. 入力X：入力系列のT個のトークン表現ベクトルを並べた行列

    2. マルチヘッド自己アテンション
      マルチヘッド自己アテンションで各トークン表現を更新します。

    3. トークン位置ごとにFFNを逆伝搬
      Nブロック分繰り返したのち、$${X^(N)}$$を最終出力とします。
      →Decoderの相互アテンション用出力

  • Transformer-Decoderブロック（×６回）

    1. 入力トークン行列Y：
      前フレームまでの予測$${y_t}$$を、Nフレーム並べた行列

    2. マルチヘッド自己アテンション
      $${Q=Y, K=Y, V=Y}$$の入力で各ヘッドを並列実行し、中間出力$${Z}$$を得ます。

    3. マルチヘッド相互アテンション
      $${Q=Z, K=X^(N), V=X^(N)}$$で各ヘッドを並列実行し、入力系列の符号$${X^(N)}$$から、予測に対応するコンテキストを取り込みます。

    4. トークン位置ごとにFFNを逆伝搬して、各ベクトルの表現を変換

  • 旧来のseq2seqと同様に、あらたに予測されたトークンを次のフレームの入力$${K}$$としてフィードバックし、全体を自己回帰的に実行します。
    [EOS]トークンが予測されるまで繰り返します。

旧来のアテンション手法とTransformerで提案された手法の違い

以下は従来手法とTransformerのアテンションの相違点をまとめた表です。
（CVMLエキスパートガイドより）

9. 改善モデルTransformer-XL

オリジナルなTransformerは、マルチヘッドアテンションを主部品にしているので、固定長コンテキストしかモデリングができないという問題がありました。

Transformerは、入力系列行列Qと出力系列行列Vとの間で、QKVアテンションを行います。
その際に各ヘッドがドット積行列計算ベースなので、系列長の可変具合にうまく対応できません。

つまり、自己アテンションの採用により、長期コンテキストはアテンションでとらえやすくなったが、固定長コンテキストしか学習できないという問題点がありました。

そこで、Transformer-XLでは、TransformerにRNN的な時系列遷移を半分（完全にではない、の意味）追加することで、可変長コンテキストに対応するようにしています。

10. おわりに

今回はマルチヘッドアテンションについて勉強しました。
一番長かったですが、個人的にはかなり面白かったです。

元々、Transformerはアテンションの計算を並列で実行できること、それまでのseq2seq with attentionよりも長いコンテキストを扱えることは知っていたのですが、具体的にどんなアルゴリズムで、何をどう計算しているのかは知らなかったので、興味を持っていたんですよね。

ちなみに今回一番「へー！」ってなったところは

i行j列目の要素は、i番目のクエリトークンとj番目のキートークンの間の関連性を表します。

という部分でした。
中々よくできてますね・・・

次回はいよいよ、Transformerについて勉強しようと思っています。
もしかしたらニューラルネットワークにおける「層」になるかもしれません。
それでは。

進捗上げてます

「#AIアイネス」で日々の作業内容を更新しています。
ご興味がお有りでしたらぜひ覗いてみて下さい。

参考


この記事が気に入ったらサポートをしてみませんか？