№8　MEDIAN関数

MEDIAN関数　とは

MEDIAN(メジアン)
機能：　数値の中央値を求める。
対応Ver：365　2021　2019　2016　2013　2010
構文：　MEDIAN（数値1, 数値2, ..., 数値255）

使い方

MEDIAN関数は、複数の〔数値〕の中央値を求めることができる関数です。
〔数値〕には直接数値を入力しても、セルを指定しても、セル範囲を指定しても動作します。
そもそも、中央値とはなにかも含めて説明しましょう。

平均値・中央値・最頻値　とは

複数の数値を分析するうえでよく使われるのが

• 平均値

• 中央値

• 最頻値

この３つで、これらを代表値と呼びます。
平均値は、みなさん馴染みがあると思いますので割愛します。
中央値、最頻値については聞き覚えはあるかもしれませんがちゃんと理解している人は少ないのではないでしょうか。

平均値を求める際、対象の数値の中に突出して大きい数値または小さい数値があり、参考にならない平均値が割り出されてしまうことが多々あります。
よくメディアで「○○歳の平均年収は1,000万円！」といった情報が流れてきますよね。これが代表的な例です。
まずは下の表を見てみましょう。

Aさん～Eさんの平均年収を集計した表ですが、
どちらの集計も平均年収は1,000万円と求められます。
右表は「平均1,000万円！」と言われてもしっくりくると思いますが、
左表では「Eさんがめちゃくちゃすごいだけじゃん…」となりますよね。
このように平均値は、データ全体の特徴を把握するには便利なものですが
極端に外れた数値（外れ値）があると大きな影響を受けてしまうことがデメリットです。

そんなときに使われるのが中央値です。
中央値は、数値を小さい順（もしくは大きい順）にならべ替えたときの真ん中の数値を指します。
先ほどの表をもとに見てみましょう。

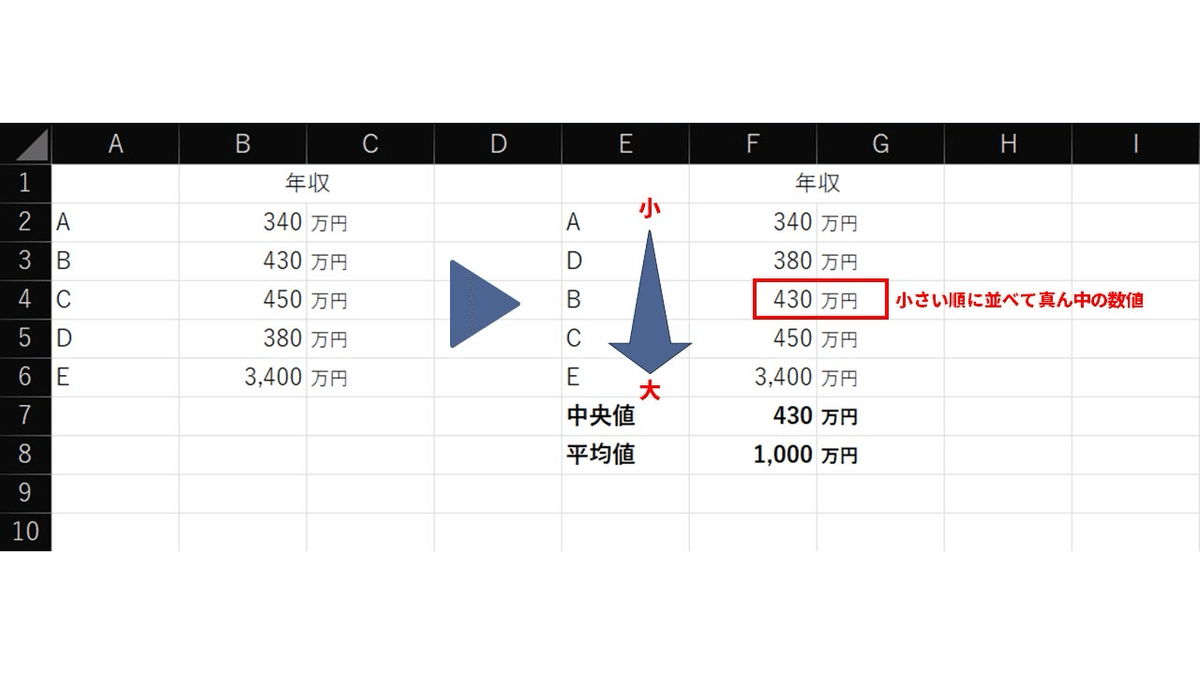
5人の年収の中央値は「430万円」という結果になりました。
いかがでしょうか？こちらのほうがしっくりきますよね。
少し話は戻りますが、メディアでいう平均年収は大きいほうに突出している人もいれば小さいほうに突出している人もいるのであまりあてにならないのです。
しかし、中央値は全体のデータから計算する数値ではない（＝外れ値を無視している）ため、全体の推移を確認することは不得意なので使い分けが必要です。
また、対象のデータ数が偶数の場合は真ん中の2つの数値の平均値が中央値となります。

それでは最後に最頻値です。
最頻値は、もっとも多く出現した数値を指します。
こちらも同じく表を使って見てみましょう。

5人の年収の最頻値は「450万円」という結果になりました。
100万円台が3人もいるため、中央値の「440万円」もやや説得力が落ちてしまっているのがわかるかと思います。
このように最頻値は外れ値の影響を受けにくく、分布に隔たりがある場合に実態を把握することができます。
しかし、データ量が少ないとまったく参考にならないのでやはり使い分けが必要です。
※数値が1個ずつしかないデータではすべての数値が最頻値となってしまいます。

それぞれにメリットとデメリットがあるので分析やプレゼンを行う際は一つに偏らず、様々な観点から確認をすると良いでしょう。

前置きが長くなってしまいましたが、最後に最頻値を求めることができるMODE関数と合わせて構文も説明しておきましょう。

合わせて覚えておきたい関数

• AVERAGE関数　平均値を求める。

• MODE関数　最頻値を求める。

MODE関数　とは

MODE(モード)
機能：　データの最大値を求める。
対応Ver：365　2019　2016　2013　2010
構文：　MODE（値1, 値2, ..., 値255）

MODE関数は、複数の〔数値〕の最頻値を求めることができる関数です。
〔数値〕には直接数値を入力しても、セルを指定しても、セル範囲を指定しても動作します。

まとめ

平均値(AVERAGE関数)
メリット:全体を把握しやすい
デメリット:外れ値の影響を受けやすい

中央値(MEDIAN関数)
メリット:外れ値の影響を受けにくい
デメリット:全然を把握しにくい

最頻値(MODE関数)
メリット:外れ値、分布の偏りの影響を受けにくい
デメリット:データが少ないと機能しない

応用できる関数

MEDIAN関数・MODE関数ともに、集計の幅を広げられる以下の関数を覚えておくと良いでしょう。

• AGGREGATE関数

※AGGREGATE関数の〔集計方法〕にある【MODE.SNGL関数】は【MODE関数】の互換性関数ですので同様の使い方・機能です。