
量子コンピュータの検索アルゴリズムの可視化に挑戦(完成動画あり)
2023年の初投稿です。1月もあっという間に半月が過ぎてしまいました。
今年も量子関係の記事を定期的(1ヶ月に2記事が目標!)に書いていきたいと思います。
さて、今回のテーマは、量子コンピュータの検索アルゴリズムのアニメーション動画作成に取り組んだ話です。
経緯としては、昨年、量子コンピュータの教育プログラムに参加し、色んな「やりたいこと」が出てきてpythonの勉強を始めたのですが、そのアウトプットの一環で、「量子コンピュータの計算の原理や速さのイメージを可視化できたらアウトリーチ的な活動に使えるのでは?」と思って作成してみようと思ったのがきっかけです。
今回は、量子コンピュータのアルゴリズムの中で、どんな教科書にも載っていて、量子の性質をどのように利用しているか直感的にわかりやすくて、個人的に一番好きなアルゴリズムである「グローバーの検索アルゴリズム」の可視化にチャレンジしました。
ちなみに、動画はpygameというpythonのゲーム開発ライブラリを使用して作成しました。
ちょうど、pygameでゲームを作りながらpythonを勉強するための書籍がkindle unlimitedの対象になっていたので、それを参考書にしながら勉強しました。
前置きが長くなりましたが、完成品はこちらに公開しています。(Noteに動画を埋め込みたいだけのためにYouTubeで公開)
以下、グローバーの検索アルゴリズムと動画の解説になります。
グローバーの検索アルゴリズム解説(簡単に)
※このセクションは、グローバーの検索アルゴリズムを知ってる人は読み飛ばして頂いて構いません。
グローバーの検索アルゴリズムについては、👇の記事に詳しくてわかりやすい解説記事がありました。本記事では、ここから引用もしながら簡単に解説します。
検索アルゴリズムと問合せ回数の削減
そもそもグローバーのアルゴリズムとはデータベース検索問題と呼ばれる問題を解くためのアルゴリズムです。
…
この問題は例えば0,1からなるn桁の暗証番号を当てる問題ととらえることが出来ます。
具体例で考えるとわかりやすいので、n=3とします。
0と1からなる3桁の暗証番号であれば、
000
001
010
011
100
101
110
111
の8パターン(2の3乗)の暗証番号が考えられますね。
この8パターンのうち、いずれかの暗証番号のかかった鍵を解錠しようとすると、上から順番に一つずつ試していって正解にあたるまで探索を繰り返すことになります。
従来のコンピュータ(量子コンピュータと対比するため、以下では「従来型コンピュータ」と呼びます。)でのナイーブな探索手法は、このように、暗証番号というデータベースから、所望のデータを一つ一つ順番に探索するアルゴリズムが考えられます。
ひとつ目で正解に当たることもあれば、最後まで正解が出ないこともあるので、データベースへの問合せ回数は、平均すると8/2=4回になりそうです。
一般のnで考えると(2^n)/2回ということになります(nは暗証番号の桁数)。
量子コンピュータを使ったグローバーの検索アルゴリズムでは、この問合せ回数が√(2^n)回になることが証明されています。
例えば、n=20、つまり、2^n ≒ 100万 個のデータがあったとすると、量子コンピュータでは、問合せ回数を約1000倍削減できることになります。
つまり、量子コンピュータでこのようなデータベース探索をすると、従来型コンピュータよりも高速に計算を処理できることになります(問合せに要する通信時間等を規格化した条件の下で)。
グローバーの検索アルゴリズム
先ほどのデータベース検索問題の例(n=3)で考えます。
量子コンピュータでは、量子力学の「重ね合わせ」という性質を使い、データを確率的に保存、取り出すことができます。
暗証番号の000, 001…, 111のデータは、量子コンピュータ上では、各データに"取り出せる確率"が割り振られているということです。
例えば、各データに等しい確率が割り振られていたとすると、データ数は全部で8個なので、
000 → 1/8の確率で取り出せる
001 → 1/8の確率で取り出せる
…
111 → 1/8の確率で取り出せる
のように、データベースに問合せた時、取り出されるデータが確率的に決まります。
従来型コンピュータでは、一回の問合せで一つの所望するデータを取り出しました(1番目のデータを取り出して、と問合せたら、1番目のデータのみを取り出せる)。
量子コンピュータでは、確率的にデータの保存・取り出しをすることで、一回の問合せで、全てのデータの中から、確率的に1つのデータを取り出せます。
ただし、上記のようにそれぞれのデータが等しい確率で保存されていたら、ランダムにどれか一つ取り出されるだけです。
これでは、一つずつ問合せる従来型コンピュータと変わりません。
正解の暗証番号を見つけるには、正解の暗証番号を取り出す確率だけが大きく、それ以外の暗証番号を取り出す確率は小さくなければ、意味がありません。
グローバーの検索アルゴリズムは、この確率を賢く操作し、少ない回数の操作で、正解の暗証番号のデータの確率を大きく、それ以外の暗証番号のデータの確率を小さくするアルゴリズムです。
この「少ない回数の操作」の回数が√(2^n)となり、高速な計算が実現されます。
冒頭に紹介した記事に、これを視覚的に表示した図がありました。わかりやすかったので掲載しておきます。

出典:https://www.investor-daiki.com/it/grover-why-important#toc4
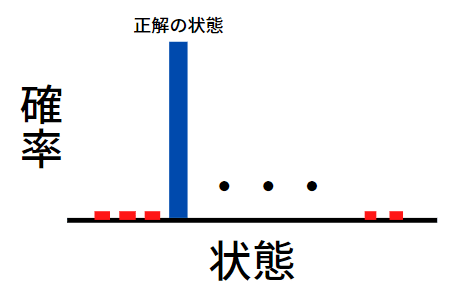
出典:https://www.investor-daiki.com/it/grover-why-important#toc4
動画の説明
グローバーの検索アルゴリズムを念頭においたうえで、動画の解説をします。
設定
コンピュータ内にはいろんな色の●が描かれたカード16枚のデータベースがある
このベータベースから、所望の色のカードを検索したい(今回の動画では黄色の●カードを検索。正解は上から3段目、左から2列目にある)
従来型コンピュータ(左側)
従来型コンピュータは順番に検索
カードの色を問合せる信号を出し、信号を受けたコンピュータがカードをめくって色を確認し、検索者に信号を返す
色が違ったらやり直し
正解カードに辿り着くまで上記を繰り返す
問合せの試行回数は正解のカードが出るまで。動画では10回の問合せで正解カードを発見
量子コンピュータ(右側)
グローバーの検索アルゴリズムで検索
カードに割り当てられた確率をカードの透明度で表現。確率が低いと透明度が上がり(カードが薄くなる)、確率が高いと透明度が下がる(カードが濃くなる)
初期状態は全てのカードが等しい確率で出る。全てのカードが同じ透明度(薄さ)
一度の問合せごとにカードの確率が変化。正解カードの確率が高くなり、それ以外のカードの確率が低くなる
十分に正解カードの確率が高まったところでデータの取り出しをすると、正解カードが取り出される
今回は以上です。
量子コンピュータをもっとわかりやすく直感的に伝える方法がないのか、今後も考えたいと思います。
この記事が気に入ったらサポートをしてみませんか?
