アンテナにおける磁荷と磁流

　今回は完全に自分用です。まず、マクスウェル方程式を知っていることが前提の議論になります。

１．アンテナにおける磁荷と磁流

　自然界の電磁場はMaxwell方程式に従います。このMaxwell方程式は電場と磁場を使った表現で以下のような4つの偏微分方程式にまとめられます（電流密度がjではなくiなことにいまだに慣れない…）

　このうち(2)式は磁気モノポールが存在しないことを示しおり、それに対応して、(4)式に磁流密度が現れていません。
　しかしアンテナの教科書を読んでいると、電場と磁場の対称性を考えた方がわかりやすくなる、という人間の勝手な理由で磁荷ρ_mと磁流i_mを追加して以下の式のようにしてしまっています。

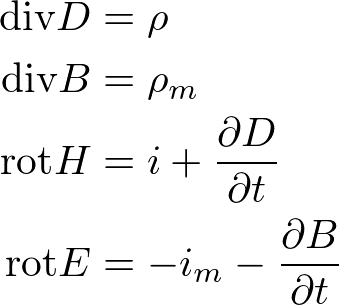
　初めて見たときはびっくりしました。工学というのはどういう世界なのかと。しかし、確かに理論的位置づけがあると考えられるのでここにメモ代わりに残したいと思います。

２．まずは磁荷から

 　いかに磁荷を考えるとは言え、自然界に磁気モノポールが存在しないことには変わりありません。そのため(2)式の左辺の磁束密度Bの一部を磁荷と考える必要があります。そのため、磁束密度Bを等価的な磁荷に対応するB_mと、それ以外のB_0に分けることします。（図はとりあえず書いてみたイメージ。あっているかはまだちょっと自信ない。）

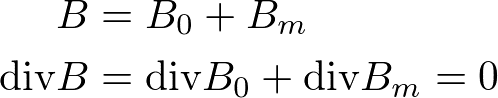
　ここで、磁荷ρ_mを以下の式で定義することで磁荷の存在するMaxwell方程式を考えることができます。

３．磁流密度

　次に磁流密度について考えるため、(4)式についても磁束密度BをB_0とB_mに分解してみます。

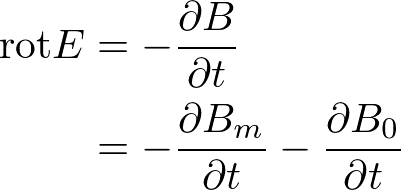
　ここで、以下のように磁流密度を定義することで磁流密度を含めたMaxwell方程式を再現できます。

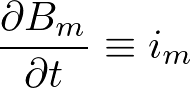
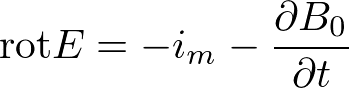
４．磁荷と磁流密度の間に連続の式も成り立つ

　ここで磁流密度の定義式の両辺に発散をとることで、なんと磁荷の連続の式が成立します。ここまでくると磁荷と磁流密度を仮想的に考えることが正当化された気がしてきます。

５．何がしたいのか

　今回のような磁荷と磁流密度の導入は、磁束密度の一部を磁荷と置き換え、電界の一部を磁流密度と置き換えただけになっています。なぜこんな置き換えをするのかというと、アンテナの特性を考えやすくするためです。今回の議論では電磁界の一部を好きに抜き出して置き換えることができるところがミソで、アンテナの放射に寄与する電界を磁流密度に置き換えることでアンテナの特性が計算しやすくなるのです。具体的には、磁荷と磁流密度を考えると磁界系のアンテナ（たとえばスロットアンテナ）を考える際に似たような電界系のアンテナ（ダイポールアンテナ）の結果をそのまま使うことができる、というようなことがなされます。

補足．Diracの磁気モノポールとの関係

　磁気モノポールといえば、Diracの磁気モノポールを思い出す人もいるでしょう。しかし、Diracの磁気モノポールはdivB=0にも関わらず磁荷が出てくるというのがミソで、アンテナの人たちが言う磁荷とは全然別のものです。Diracの磁気モノポールについては境界条件（ゲージ接続）のところから導出されるもので、この辺を深堀していくとトポロジカル絶縁体などの先端物理の世界が広がっており、面白いと思います。