京大理系数学2022を解く　大問5

2022年に実施された京都大学の入試問題の数学(理系)の問題について、解く上でのポイントや実際に解く時の視点を書き連ねていく。

大問5

数Ⅲが混じった関数の問題だが、(1),(2)は難しくない。(3)だけ他に比べると難易度はあがるが難しいとまではいかないだろう。

まずは(1)の$${S}$$および、$${f_{(t)}}$$だが、これは何の工夫もなくすぐに求まる。

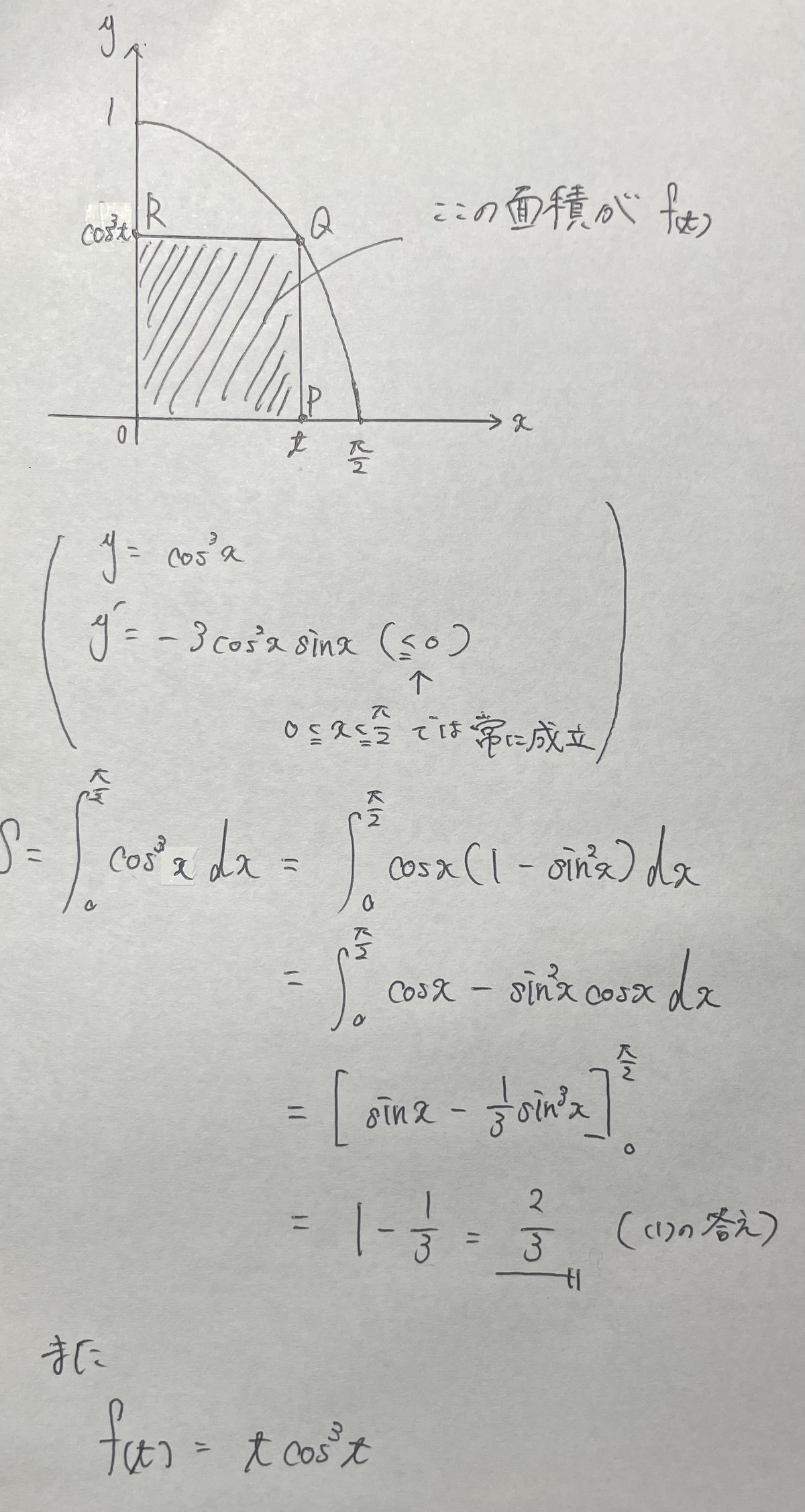
$${{\cos{x}}^3}$$の積分だが、これは数Ⅲの積分としては基礎レベルだろう。$${{\cos{x}}^n}$$の積分の漸化式でやるのと同じように$${{\cos{x}}^2=1-{\sin{x}}^2}$$を使ってやれば微分形の接触の形とただの$${\cos{x}}$$の積分が残る。3倍角の公式を使う手もあるが別にそんな公式を使うまでもないだろう。

続いて(2)だが、これも数Ⅲの微分では頻出の問題である。よく出てくるので必ずできるようにしておきたい。

2回微分すると、2回目の微分の際にどうくくっても$${t=0}$$か$${t=\frac{\pi}{2}}$$で定義できなくなる。その辺の論証が少し怪しくなってしまう。(多分丸をくれるとは思うが、はっきりとは言い切れない。）ということで次のようにして回避する方法もあるが、今回のように回避しきれない場合もあるので一応両方見ておいてほしい。

またどちらの解答方針についても言えることだが、(むしろ関数を扱う問題全般に言えることではあるが)必ず区間の端の値と極値に注意するように心がけておきたい。
そして(2)の後半だが、$${\alpha}$$が満たす条件さえしっかり把握できていれば何も難しくはない。$${\alpha}$$が満たすのは$${{f_{(\alpha)}}'=0}$$である。これを使えばいい。

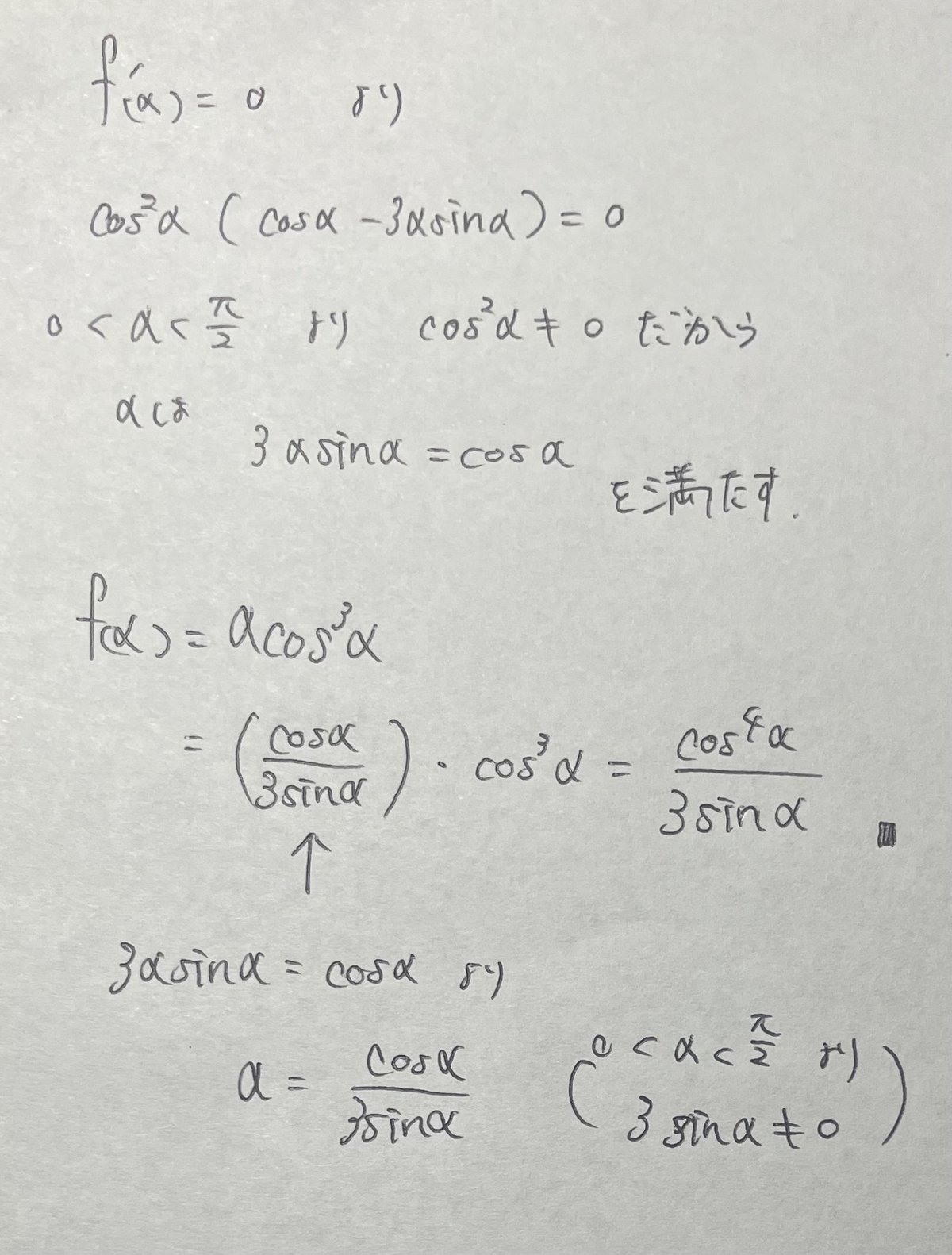
変形についてはゴールに近づけることを意識すれば自然とできる。

最後に(3)だが、ここで必要なのとりあえずまず最初に気づくのは(2)で示すことを要求された謎の式である。やっぱりこれを使うべきではなかろうかと思うだろう。

すると多少具体的な不等式が出てくるのだが、これ以外に$${\alpha}$$についての条件は$${0 < \alpha < \frac{\pi}{2}}$$だから、一旦次の仮説を立てる。

これが成り立てば$${\alpha}$$の時にも適用できる

ただこの仮説は微分したりせずとも$${x→0}$$の極限を取れば無限大に発散するため成り立たないとわかる。
となると次に考えるのは$${h_{(x)}=\frac{9}{16}}$$となる$${x}$$である。なぜこれを考えるのかというと、もしこの$${x}$$が具体的に分かれば$${\alpha}$$との大小関係と$${h_{(x)}}$$の関数の増減さえ調べてしまえば示せる。またこういうときの$${x}$$は99%有名角(三角関数絡みじゃなかったら簡単な有理数)に限るので有名角がダメなら次の手段を考える。(大体ここまででどうにかならない場合には他にも誘導が入っている。）

すると$${h{(\frac{\pi}{6})}=frac{9}{16}}$$となったのであとは$${\alpha}$$との大小関係と$${h_{(x)}}$$の関数の増減を調べてしまえば解答が書ける。(このとき解答を書くと最初から急に$${\frac{\pi}{6}}$$が出てくるので数学の解答あるあるの「どこからそれが出てきたのか？」みたいな解答が出来上がる。)

ということで解答の要素がすべて出揃ったので終わりだが、この問題は(2)までは必ず取りきりたい。(3)が比較的難しく、2022年の京大理系数学の中では難しい部類にはなるのだが、ただこの年の京大理系数学はおそらく他年度と比べて簡単なのでこのレベルの問題も練習の間は取れるようにしておきたいところだろう。

大問6へ続く。