東大理系数学2022を解く 大問4
2022年に実施された東京大学の入試の理系の数学の問題を解くときの思考を明らかにしながら解き進めていく。
前回の記事から2週間近く空いてしまったのだが、僕の怠惰と夏風邪のコンボが決まってしまったためである。怠惰に関しては反省しているが、体調不良にはくれぐれも気をつけてほしい。
大問4

三次関数と直線にまつわる数Ⅱの微積分からの出題で東大はここ数年こういうタイプの数Ⅱの関数絡みの問題を出題している(2024年の大問4や2023年の大問3など)ので東大の受験生なら必ずといっていいほど対策すべき分野になるだろう。理系の微積分と言われれば結構な場合数Ⅲからの出題になる。(実際僕が取り扱った問題のうち、数Ⅲの微積分は少なくとも10問以上ある。)しかし、東大は数Ⅱから、つまりは文系数学で見られそうな問題が出題されやすい。(本問については一部数Ⅲも使うことにはなるが。)
ということでやっていこう。
まず(1)からだが、こういう問題ではやっぱり何を示すべきか、何に辿り着けばOKかをちゃんと捉えておきたい。得意な人はおそらくあっさり解ききるのだろうけれど、こういった問題がそこまで得意じゃない人は適当に解き進めてしまうと何をすればいいのか、果たしてゴールに近づいているのかが分からず混乱してしまう。(実際僕もそこまで得意ではないからボーッと解いてると混乱しかねない。)だからこそ丁寧に解き進めたい。
まず、やっぱりこんな抽象的なままじゃ議論が進められないので点Pの座標を$${(a,b)}$$とし、直線lを$${y=k(x-a)+b}$$とする。(傾きが$${k}$$で点Pを通る直線)
実際、文字設定しようものなら点Pにしなくたって傾きと切片さえ文字置きすれば今回の僕の手法よりも文字が少なく済むのだが、示すべきことを見失わないためには点Pの座標を文字置きした方が絶対に良い。仮に切片を文字置きすると、「全ての点Pで」の言い換えに詰まってしまう。一方で座標を文字置きすることで誰でも簡単に言い換えができる。
あえて文字を少し多めに設定するのは珍しいのだが、数学の問題を解く時、何を文字で置くのが最善かを常に考えたい。慣れないうちは間違えることも多いかもしれないが、慣れてくると実際に手を動かす前に良し悪しが分かるようになってくる。
話を戻そう。
示すべきこと:「点Pを通る直線lで、曲線Cと相異なる3点で交わるものが存在する」というのはより具体的に次のように言い換えられる。
全ての実数$${a,b}$$に対し、ある実数$${k}$$のとき、次の連立方程式を満たす実数$${(x,y)}$$の組が3組存在する。
$${y=k(x-a)+b}$$
$${y=x^3-x}$$
ここでの言い換えは「全て」と「ある」を上手く使いこなせていればできるものである。数学は理系科目の筆頭だが、意外と国語力が問われるのでそれも数学で必要な分くらいは養っておきたい。
また、2式を連立させることでもう少し簡単にできる。
全ての実数$${a,b}$$に対し、ある実数$${k}$$のとき、次の方程式を満たす実数$${x}$$が3つ存在する。
$${x^3-x=k(x-a)+b}$$
こうなれば、全て片方の辺に寄せて関数と見て処理していけばいいだろう。一応$${x≠a}$$の場合だけ別にして$${k=\frac{x^3-x-b}{x-a}}$$として定数分離することもできなくはないが、どう見ても右の関数の微分が面倒だし、そもそも場合分けも面倒だしということで今回はそうしないことにする。(グラフから視覚的に$${k}$$がどの範囲のときにある時にこの方程式が相異なる3解を持つかを判定できる利点はあるのだが、それ以上に計算が面倒だと僕は思った。場合によっては定数分離した方がいいケースもある。)
ということで、微分及び増減表を書いてみると次のようになる。

このように$${k}$$の値によって関数の増減が変わってくる。そして今回は方程式$${x^3-x=k(x-a)+b}$$が異なる3つの解を持たなければならないのだから、$${k>-1}$$の時に焦点を当てていいだろう。あくまで全ての$${k}$$で3つの異なる解を持たなければならないのではなく、何か1つ、3つの異なる解を持つ$${k}$$を持てばそれでOKだからである。別に$${k \leqq -1}$$の場合に固執する必要はない。ということで$${k>-1}$$の時についてもう少し話を進めてみると次のようになる。

ポンポン示すべき事実をすり替えている(言い方が悪いがただ言い換えているだけである)のだが、着いてこれているだろうか。3つの相異なる解を持つには極大値が正、かつ極小値が負である必要がある。例えばここで何かしら文字が具体的な数値に置き換わっていたら極大値、極小値で議論しない手もあるのだが、ここでは極値で議論するしかないだろう。(例えば$${b}$$が正なら極大値の方の議論は要らなくなる。)
あとは画像にある2つの不等式をともに満たす$${k}$$の存在を示すのだが、まず考えるのは具体的に$${a,b}$$を使って$${k}$$を表すことだが、今回$${a,b}$$には実数という制約以外なく、仮に$${a,b}$$のみの式になっても正負を判定するのは困難だろう。ということでそういった手は取れないのだが、式をちゃんと見てみると$${\frac{2}{3}(k+1)\sqrt{\frac{k+1}{3}}}$$はおおよそ$${k^{\frac{3}{2}}}$$の項であり、$${ka-b}$$は$${k}$$の次数が1次なので$${k}$$が十分大きい、つまり無限大での議論では$${a,b}$$を無視できてしまう。ということで極限を考えれば片付くと分かる。

ここで$${k}$$を正に限定し、先ほどの不等式の$${ka}$$の項を移項して両辺を$${k}$$で割ってから極限を考えるのもありだが、そこまでしなくてもおそらく丸はつくだろう。(もちろんより丁寧にはなるのだが。)
続いて(2)だが、この問題では必ず同値性が保たれているかに細心の注意を払ってほしい。この問題に限らず、基本的に軌跡・領域の問題では同値性が崩れていないか、崩れているならその部分をちゃんと補強しているかは最重要事項となる。
これまた(1)同様に問題文を具体的に言い換えると次のようになる。
実数$${a,b}$$及び$${k}$$に対し、相異なる3つの実数解を持つ3次方程式$${x^3-x-k(x-a)-b=0}$$についてその3解を小さい方から順に$${\alpha , \beta , \gamma}$$とする。($${\alpha < \beta < \gamma}$$)
その時、ある$${k}$$に対し次の等式が成立するような$${(a,b)}$$の範囲を図示せよ。
$${\int_{\alpha}^{\beta}x^3-x-k(x-a)-b dx=-\int_{\beta}^{\gamma}x^3-x-k(x-a)-b dx}$$
面積ということで積分を使って具体的に表現し、そうするために3つの解をそれぞれ$${\alpha , \beta , \gamma}$$とした。面積を求めるには範囲が必要であり、そのためにも直線と三次関数の交点の$${x}$$座標が必ず必要となってくる。そして交点を置いたからには次の式も成立する。
$${x^3-x-k(x-a)-b=(x-\alpha)(x-\beta)(x-\gamma)}$$
(新たな文字を設定した時には使うかどうかにかかわらず、必ずその文字についての情報を抜け目なく集めきらなければならない。)
ここから、その等式を変形し、何かしら条件を決定したいのだが、こう思って欲しい。
「一体何についての条件を求めるべきだろうか?$${a}$$や$${b}$$なのか、はたまた$${k}$$?もしくは新しく登場した$${\alpha , \beta , \gamma}$$なのか?」
実際どれについての条件でも領域は決定できる。$${a}$$や$${b}$$については言わずもがな、$${k}$$の範囲が決まれば(1)と似たような議論をすれば良い。また$${\alpha , \beta , \gamma}$$であっても仮に条件が決まれば$${\alpha , \beta , \gamma}$$を基点にして直線を議論すればただの直線の通過領域の話に帰着できる。
今回どれを選ぶかだが、簡単に消えなさそうなものを選ぶべきである。やっぱり、選んだからには他の文字は上手いこと消去できないと条件式が導出できない。となると、1番消去しづらいのは積分区間に入っている$${\alpha , \beta , \gamma}$$ではなかろうか?これを上手く消すのは大変そうだから、これらに関する条件を導き出したい。
「他の文字はどうするんだ」と思うかもしれないが、$${x^3-x-k(x-a)-b=(x-\alpha)(x-\beta)(x-\gamma)}$$があるおかげで実は簡単に文字消去できてしまう。ということでやってみると次のようになる。
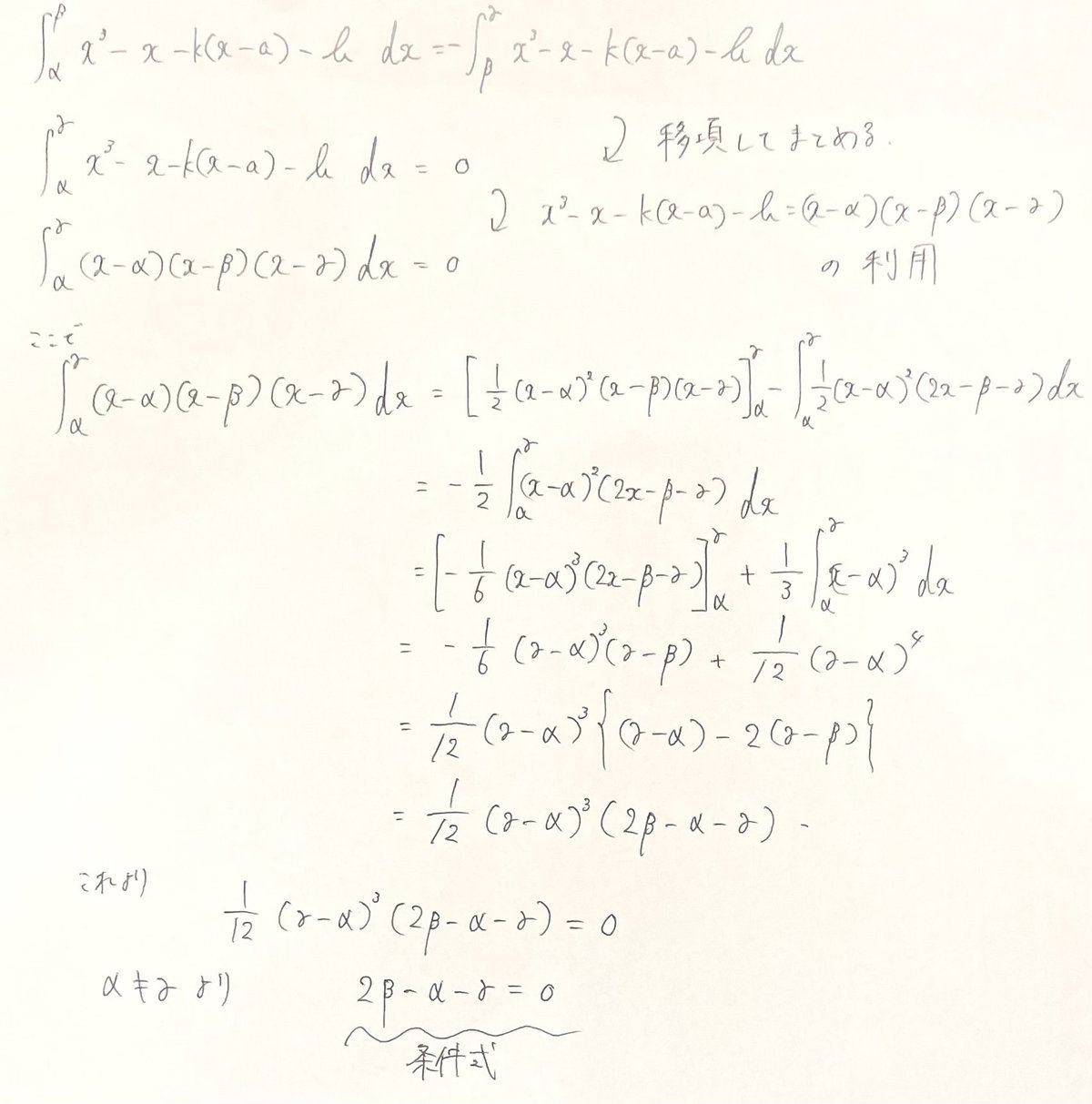
ここでの積分のコツだが、苦手な人はこういう積分ですぐに展開したくなるかもしれないが、それは悪手でしかない。もし展開すると積分こそ簡単だが、そうして出てくる式の処理がかなり厳しい。なんせ4次式の因数分解を求められるため、そう上手くいくことはないだろう。理系は文系と違って積分における引き出しの1つに部分積分があるのだからこれを上手く使うのがスマートだろう。どこを積分し、どこを微分するかだが、これまた先を見通して適切な選択をしたい。解く側として最も望ましくないのは項が大量に出てくることだから、できる限り$${x=\alpha}$$か$${x=\gamma}$$を代入して0になるように心がけると画像のようなやり方が最適と言えるだろう。
こうして条件式を出したが、$${\alpha , \beta , \gamma}$$についての条件式が出てきたのだから、それを有効活用するためには$${\alpha , \beta , \gamma}$$をかき集めたい。となれば、恒等式$${x^3-x-k(x-a)-b=(x-\alpha)(x-\beta)(x-\gamma)}$$の係数を比較し、そこから条件式を持ってこれば次のようにして答えが出る。
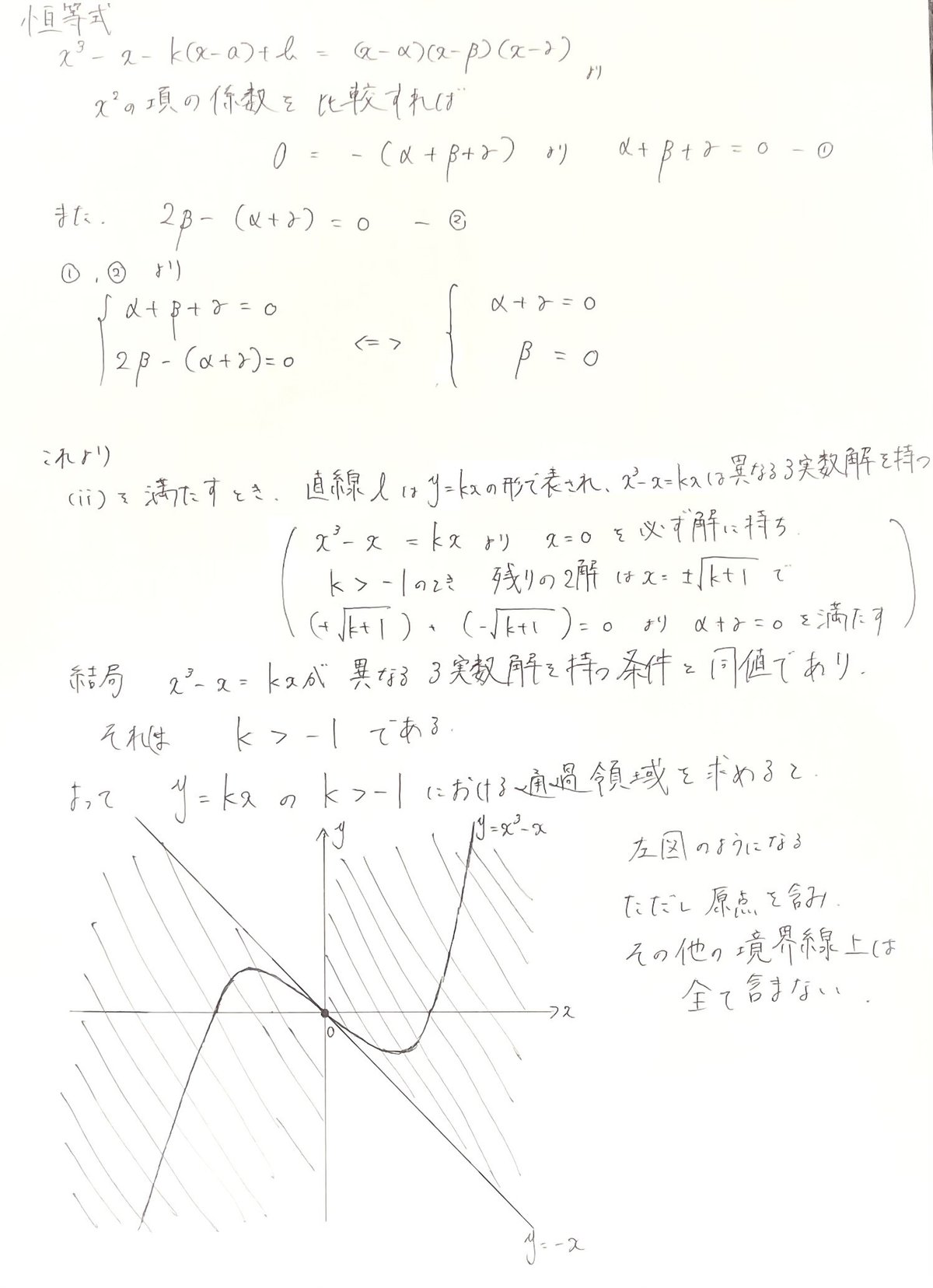
ちょっと書き漏れた部分を補足しておくと、(ⅱ)と$${l}$$が$${y=kx}$$の形で表されることが同値であるという部分について、画像では$${l}$$が$${y=kx}$$の形で表され、$${x^3-x=kx}$$が異なる3実数解を持つならば、(ⅱ)、つまり$${\alpha +\gamma=0}$$と$${\beta=0}$$を満たすという部分については説明してあるが、その逆は説明していない。ただ、この部分の論述は簡単で対偶を考えれば$${l}$$が$${y=kx+m}$$の形($${m≠0}$$)で表されるならば、$${x^3-x=kx+m}$$は$${x=0}$$を解に持たないので(ⅱ)を満たさない。だから確かに同値である。
今回は三次関数と直線にまつわる問題だったが、一見単純そうに見えて実は結構難しい。(2)については$${y=x^3-x}$$が奇関数であることなどを踏まえれば答えの予想はいとも簡単につけられるのだが、実際ちゃんと記述を書けば文字が多くて少し大変に感じた。ただ、部分ごとに見ていけば案外見慣れたことしかやっていないからこそ堅実に解き進めたい。
大問5へ続く。
