個人的入試解説 part2 東京医科歯科大2024大問3

このコーナーでは僕が普段扱う予定のない数学の入試問題の中で、個人的に記事を書きたいと思った問題を扱います。
今回の問題は2024年の東京医科歯科大学の入試問題から大問3です。

分野は数Ⅲの積分で、この問題を選んだのは巷でよく言われているking propertyなるものの紹介にちょうどいい入試問題だからである。
ということで問題に入る前にking propertyの説明をしておこう。king propertyとは次のようなものである。

要するに置換の一種なのだが、特に三角関数が絡む定積分などではこれを使うことで綺麗に解ける問題がいくらか存在する。必ず覚えなければいけないかと言われると怪しいが、時々出題されるので出てきた時には焦ることがないためにも知っておきたい。
どう使うかだが、king propertyを使って等式を作り、求めたい定積分の値を$${I}$$などとして左辺と右辺の和、つまり$${2I}$$を計算することが多い。簡単な例題で確認してみよう。

これはking propertyの有名な例題で、普通に積分しようとすると苦労するものでもking propertyを使えば簡単に解ける問題の典型例である。
ということで、これを使えば(1)の証明はあっさりと完了してしまう。

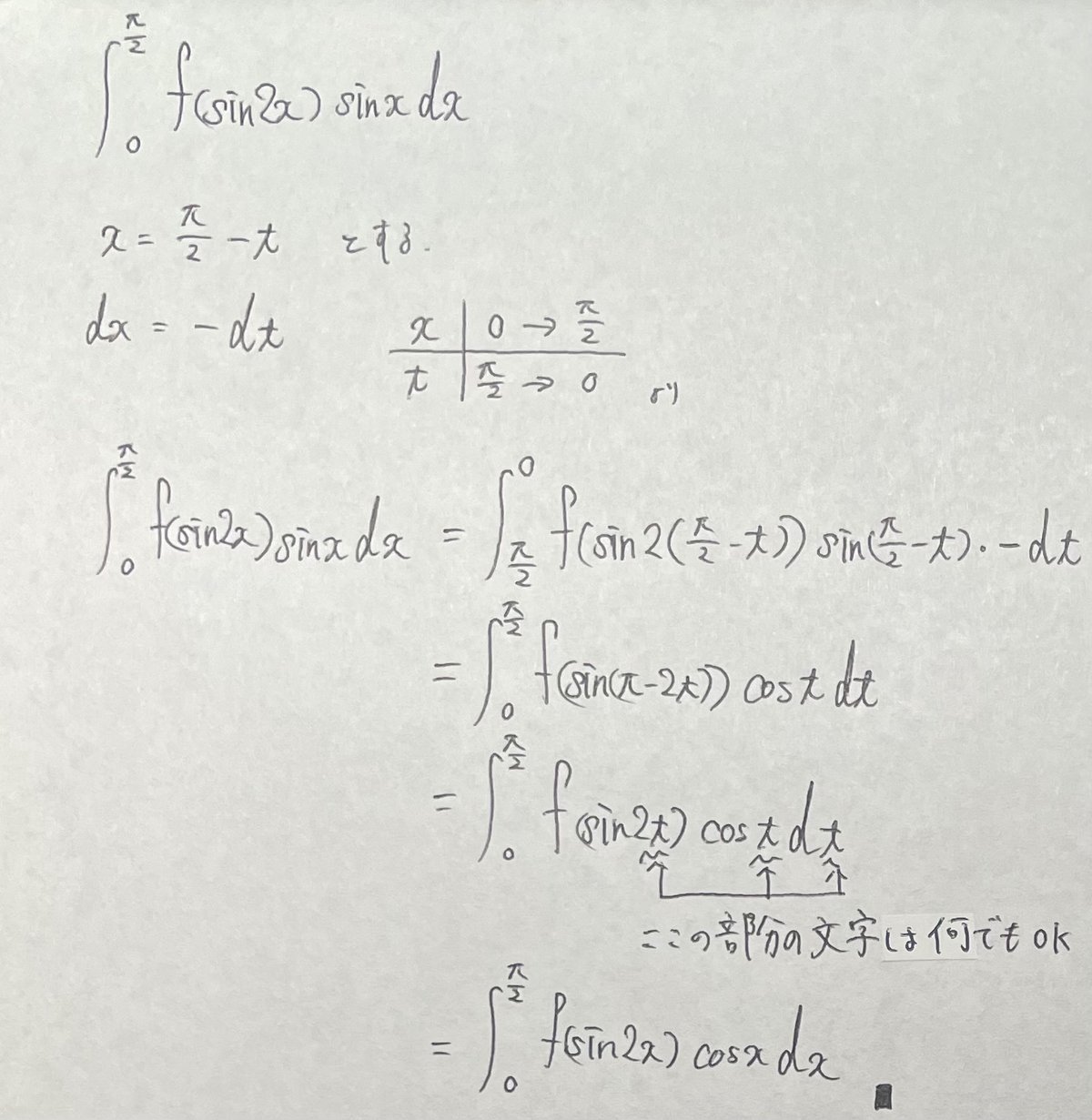
これを知らなくても、ただ置換するだけで証明できるので辿り着けるかもしれない。しかし、何しろ積分区間が同じであるがためにどう置換すべきか見抜きづらいし、そもそもking propertyを知らなかったら置換よりも部分積分などを疑うかもしれない。だから、知っているか知らないかで差がついてしまったのではないだろうかと僕は睨んでいる。(本来はこういった知識で差がつく問題は好ましくないだろう。)

続いて(2)だが、こっちでは打って変わって観察力が問われる問題となっている。
先ほどと違って積分に使われている文字が$${x}$$と$${t}$$で違うからまず置換積分を疑うだろう。どう置換するかだがやっぱり$${f_{(x)}}$$の中身をいじるのは難しいから$${\sin{2x}=1-t^2}$$となっているだろうと仮定して何で置換するかを逆算する。すると次のようにして$${t}$$の候補が決定する。

この変形は正直ちょっとだけ難しかったかもしれない。普段、逆の操作はよくやるのだが、$${1}$$に$${(\sin{x})^2+(\cos{x})^2}$$を当てはめるのは慣れていないと少しだけ厳しい。ただ、たくさん演習を積んでいれば$${1-\sin{2x}}$$という式自体見慣れてくるので頑張ったら何とかできるだろう。
どう置換するか分かってしまえばあとはそれを使えば解決する。

最後に(3)だが、ここまで来て(1),(2)を使うことはないだろうというのは流石に受験生なら勘づくだろう。ということで使って計算すればいい。((1),(2)を使わずに素直に原始関数を求めるのは不可能である。)

誘導を使い終えてからのポイントだが、$${\sqrt{1-t^2}}$$の形を見たら三角関数で置換すると上手くいくことが多い。あと、三角関数で置換したあと、分母分子に$${1-\cos{\theta}}$$をかけると積分区間に定義域の範囲外が含まれてしまう(0で割るのと同等)なのでそれだけはしないように気をつけてほしい。また、$${1+\cos{\theta}}$$の形を見たら半角の公式を思い浮かべられるくらいには普段から演習しておこう。

今回はking property(あくまで正式名称ではないから解答にはこの名称を使わない方が良い)について扱ったが、大体の場合誘導がつくだろう。しかし、誘導がついていても知っているか知らないかで差がつきかねないのでこういった置換方法があるということくらいは頭の片隅に置いておきたい。