京大理系数学2022を解く　大問6

2024年7月13日 02:23

2022年に実施された京都大学の入試問題の数学(理系)の問題について、解く上でのポイントや実際に解く時の視点を書き連ねていく。

大問6

見たら分かると思うがこれが一番むずかしい。(実は問題の解き方を説明するのもかなり難しい。)見た目で「何じゃこれは？」となってしまうので他の問題が比較的簡単なのもあって、この問題は2022年の京大理系数学としては捨て問の部類になっただろう。

さて解いていくのだが、この問題のポイントは一般項を求める数列が数列{$${x_n-y_n}$$}であるということである。数列{$${x_n}$$}及び数列{$${y_n}$$}は見るからに解くことができないから、それぞれ処理するのではなく同時に処理することを目指したい。
また、$${\cos}$$の中に$${x_n}$$があってこのままではどうしようもないから、ここにも何か手を加えたい。

この2つくらいに着目できていたらあとは素直にやってみることになる。(悪く言えば行き当たりばったりである。)
まずは$${\cos}$$の処理からやっていこう。
そもそも、$${x_{n+1}=\cos{x_n}}$$という形の漸化式は高校範囲ではどう頑張っても解けないから、この漸化式が解ける形に近づくためには$${\cos{\frac{2\pi x_n}{3}}}$$が何かしら決まった値(その値の種類は多くても大体5個以内)しか取らないとどうにもならない。(決まった値にならなかったらほぼ100%極限の問題にしかならない。)
そういう推測の元、$${\cos}$$の値になにかしら規則性を見つけたいのだが、そのためには$${x_n}$$の規則性が必要だから一旦$${x_n}$$に注目する。また、どうみても正攻法ではうまくいかないので何か法則性を見出すために$${n=5}$$ぐらいまで$${x_n}$$の値を求めてみる。

すると驚くべきことに数列{$${x_n}$$}の項は$${n \leqq 5}$$のときすべて整数になっているから、もしやすべて整数になるのではという予測がつく。一旦はこれを数学的帰納法で示してみよう。

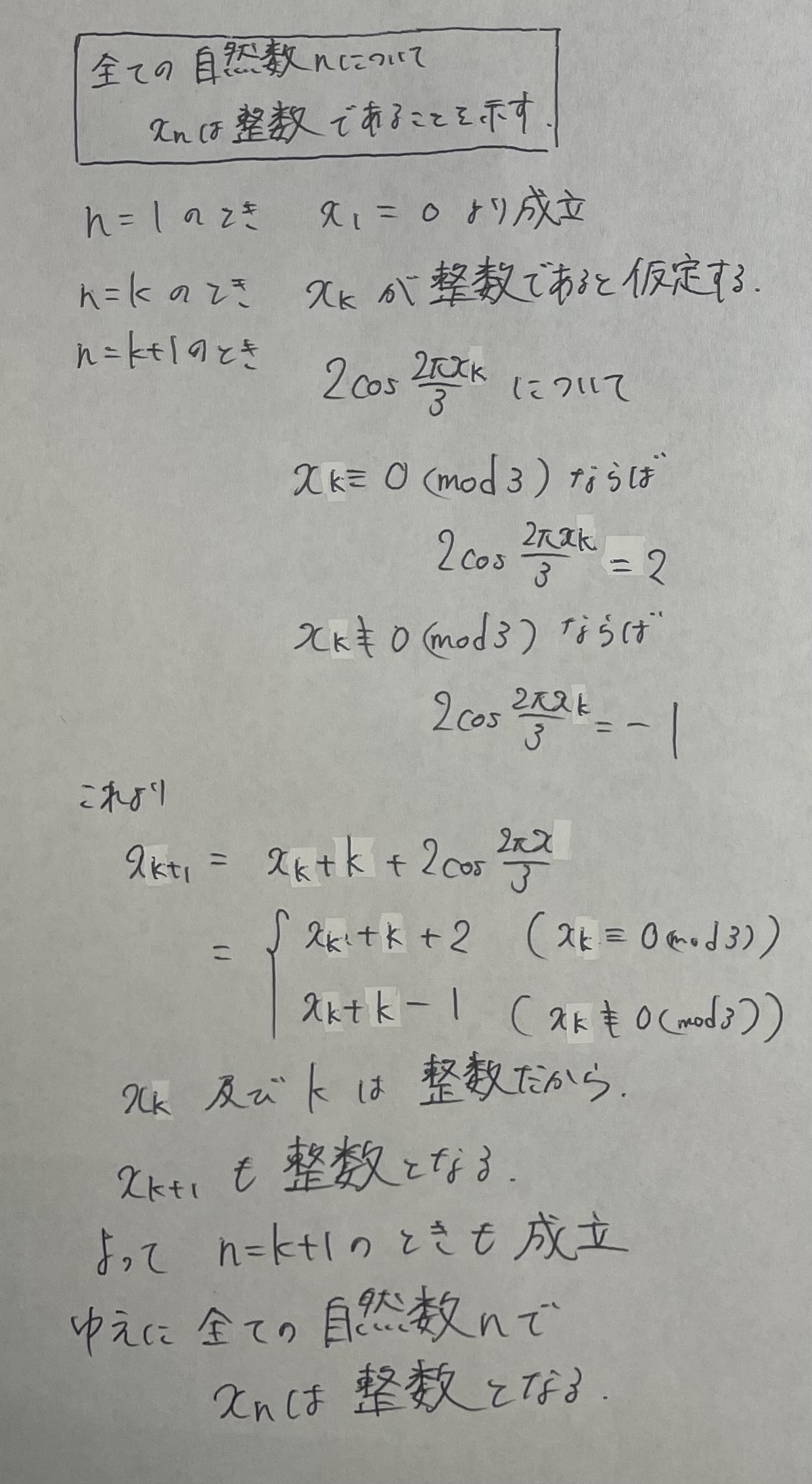
すると、数学的帰納法で示している最中に$${\cos}$$の値にも規則性が見えてきたのが分かるだろうか。実は整数だと決まれば合同式が使えるようになる(余りに注目することができる)のでそれと今回の$${\cos{\frac{2\pi x_n}{3}}}$$とが相性がいい。(整数は合同式と相性がいいことは知識として持っておこう。)

ということで、数列$${x_n}$$を次のように書き換えて$${\cos}$$を消したのでここで第一段階は終了である。

次に数列{$${x_n}$$}及び数列{$${y_n}$$}を同時に処理する方針を取りたいのだが、難点が2つある。

①$${x_n}$$を3で割った余りによって漸化式が変わる
②$${y_n}$$は$${n}$$を3で割った余りによって一般項が異なる

これらのせいで単純に$${x_{n+1}-y_{n+1}}$$を$${x_n-y_n}$$を使って表すことができない。だから、この2つを解決するようにしていくしかないだろう。
どっちから手をつけるかだが、①に手をつけるべきだろう。メタ的にはなるが、$${x_n}$$を3で割った余りに規則性がなかったらほとんどどうにもならないので、おそらく規則性があるだろうという希望的観測を持ってとりあえずやってみるしかない。(そもそも②はどうにもならない。)
そこで先程求めた$${n=5}$$まで$${x_n}$$の値で見てみる。

$${n=3}$$のとき以外はすべて3の倍数になっているから次の仮説を立ててみよう。(不安なら$${n=10}$$くらいまで調べてもよい。)

$${x_n}$$を3で割った余りは
$${n}$$が3の倍数でないとき、0
$${n}$$が3の倍数のとき、1 となる。

(この際、「本当にそう言えるのか？」とか考える人がいるだろうが、この手の問題は上手くいきそうなものを試すしかないからとりあえずやってみようの精神で挑んでほしい。)

すると、これは実は正しく、数学的帰納法を使えば簡単に証明できる。

これより数列$${x_n}$$の漸化式は次のように書き換えられる。

そして、数列$${x_n}$$も$${n}$$を3で割った余りによって漸化式が異なることが判明したことで、一旦無視した②も解決できそうになったなと感じる。
②をどうやって解決するかだが、作りたいのは$${x_n-y_n}$$の形だから、$${x_n}$$の漸化式と同じ形にしたい。だから、あえて普段とは逆に次のような操作をする。(これは知識とかそんなたいそうなものではないし、覚えることでもない。)