
Numbers & Numerals
I've learned that there are many articles which talk about numerals (number symbols) 数字 in note community such as
Thinking about the meaning of numbers… 数字の意味を考える。その心とは…
Attachment to Numbers 数字への愛着
Cursed by the numbers 数字に呪われている
whatever...
and that's why I dare to use tags #数字 and #好きな数字 in this article.
In addition, number of those articles with Kabbalah numerology カバラ数秘術 in the title appears to be just enormous.
I definitely respect Kabbalah, and I won't deny Gematria, which I'm afraid does not cause me to get excited, but I don't have any interest in what is called numerology 数秘術. I know it may seem malicious and prejudiced for writing this way...
Then, I have realized that those authors (in the note community) do discuss on numerals and numbers interchangeably and not care difference between numbers and numerals at all. For them, integers, rational numbers or transcendental numbers do NOT matter (probably), but I'm not supposed to be critical.
Being a numberphile, those article sometimes come into my attention, but I'm afraid I instantaneously lose my interest to continue reading...
As I wrote in the following article
https://note.com/roshanak/n/n112512af5a19
I specialized in Algebraic Topology but not in Number Theory when I was at an institute of technology 45+ years ago, however, Number Theory, not necessarily limited to Algebraic Number Theory but also including Analytic Number Theory, has been studied so intensively for 380+ years (since the days of Pierre de Fermat) with ample fascinating results, and I innocently wish those authors do spend just a little time to look into some properties of numbers...with just a slight change in their perspective.
Why I stick to difference of numerals and numbers ? Just a few examples:
① Numbers can be expressed in multiple ways.
② There're real (and of course complex) numbers which cannot be expressed in numerals in our "standard fashion", or even known. An easy example is tan((666!)^(666!)) where tan stands for the standard tangent function (by radian). For example, 9^9 = 9⁹ = 387420489 and we can calculate tan(9⁹) = -0.94583369757852826214612547718209... however (666!)^(666!), which is called the Legion's number of the 2nd kind, is an absurdly gigantic number with roughly 1.609941 x 10^1596 digits, and we don't know its value (=number) of tangent function. Please note that the largest known prime as of today is 2^82,589,933 − 1 with 24,862,048 digits, which is nothing compared with the Legion's number the 2nd kind…well I wrote an article on Big Numbers:
Here's a graph of y = tan(x^3) with a tweak to the periodic tangent function. From this graph it's quite obvious that tan(x^3) moves between -∞ and ∞ ridiculously frequently to the extent that it no longer appears to be a graph when x glows large.
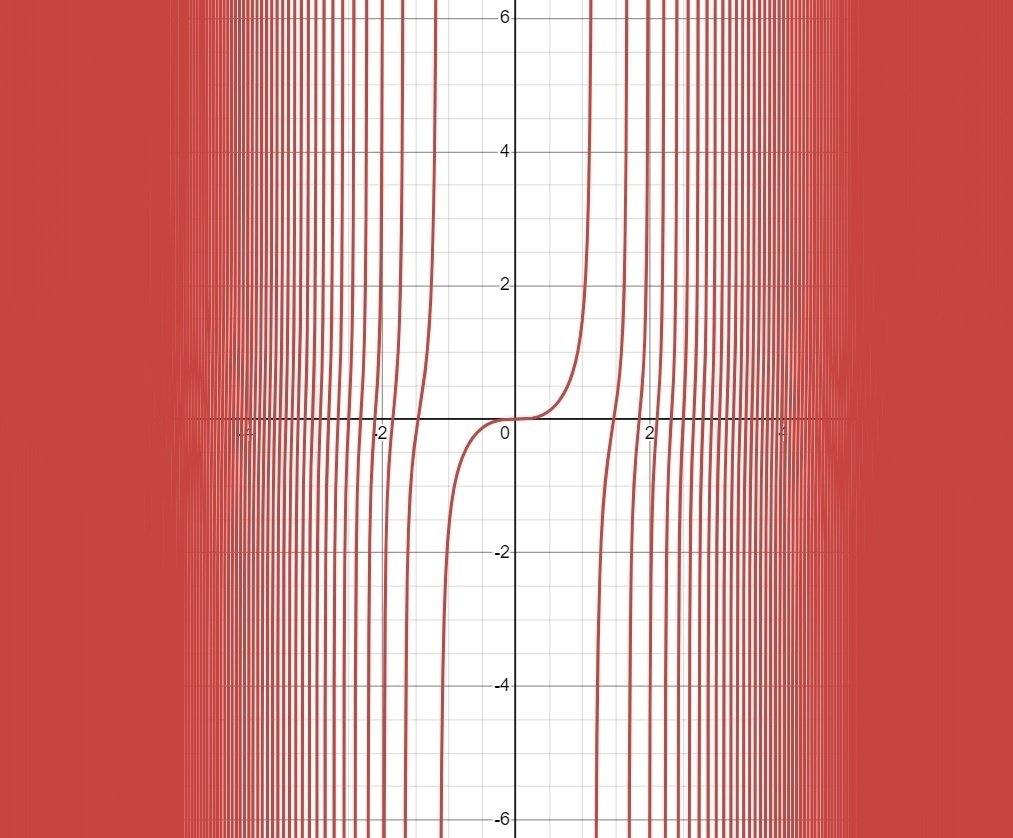
③ Eastern Arabic numerals are symbols used to express numbers in the exactly same fashion, which I would assume, as those Arabic numeral symbols we currently use in many countries.

④ There's another numeral system invented by the Maya, a sample (called Dresden Codex) is attached below via
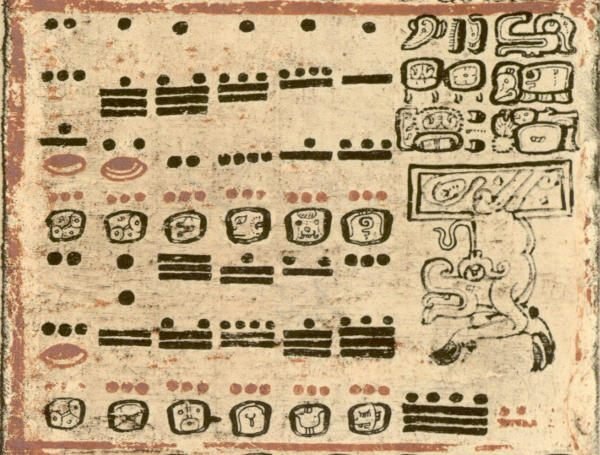
Again, I am not supposed to write in a critical tone...but I wish to shed light on some ambiguities which might contain contradictions.
The following site (Omniglot) contains numerals in various writing systems:
While I mentioned "ample fascinating results", obviously it's not true that we know everything about numbers. Here are two mind-boggling examples:
There are numbers which we even don't know whether they are transcendental or not such as ζ(3) called Apéry's constant where ζ stands for the Riemann's ζ function. While Leonhard Euler solved the so-called "Basel problem" and determined
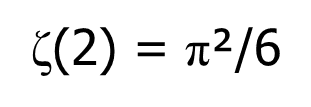
in 1734, ζ(3) was only proved to be irrational in 1978 by Roger Apéry but we still don't know if it is a transcendental number or not.

Another example is Euler-Mascheroni constant γ (gamma) which has not been proved algebraic or transcendental. In fact, it is not even known whether or not γ is irrational. One would not call it useless to pursue this particular number since it does appear in many places.
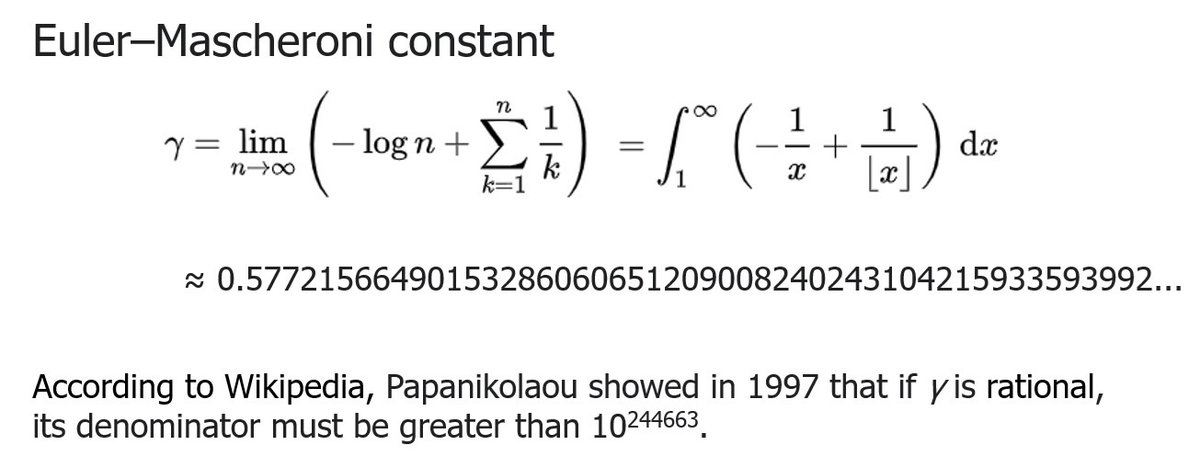
Changing our perspective a little bit, we can view a number not as an independent number but as a pattern which appears in a long sequence of digits. 142857 appears repeatedly in decimal representation of 1/7 = 0.142857142857142857142857...
We have two opposite groups of examples:
<small period>
1/37 = 0.027027027027027027027027027027... : the pattern (called period) 027 (3 digits)
1/137 = 0.00729927007299270072992700... : the period 00729927 (8 digits)
1/239 = 0.00418410041841004184100418410042... : the period 0041841 (7 digits --- exceptionally small)
<large period>
1/233 = 0.004291845493562231759656652360515021459227467811158798283261802575107296137339055793991416309012875536480686695278969957081545064377682403433476394849785407725321888412017167381974248927038626609442060085836909871244635193133047210300... : its period has 232 digits! (233 is one of full reptend primes which are the primes p such that the decimal expansion of 1/p has period p-1.)
1/4001 has period 500.
1/4463 has period 4462 (i.e. 4463 is a full reptend prime).
There's another intriguing "pattern" in particular Bernoulli numbers, but I will write about this in another article. There's one caveat. A pattern should not be confused with some kind of rule. Liouville number defined as
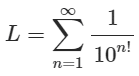
was the first explicit constant proven transcendental and is very "close" to a rational number. In a broader sense it has a pattern (or a rule) but not repeated like the period for rational numbers.
In closing, if you ask me what my favorite numbers are, my answer would be 71, 907, 1093, 433494437, 7758337633 (all prime numbers) et al. for integers and Ramanujan's constant and the first Feigenbaum constant δ to the period-doubling bifurcations in the logistic map, if not restricted to integers.
Whether it is my favorite number or not, it is extremely interesting that number 1111111111111111111 (nineteen 1's) is prime. In general, define
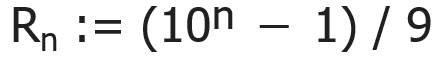
Then,

and interestingly, for n ≥ 20, prime numbers appear at n = 23, 317, 1031, 49081...
Back to my favorite numbers:
71 looks like just an ordinary prime, and a twin of (71, 73), but it is the smallest number n such that the imaginary quadratic field Q(√-n) has class number 7 and the largest supersingular prime. Supersingular primes are related to the notion of supersingular elliptic curves, which I studied, but are often referred to moonshine theory, which is a terra incognita for me.
907 appears in Hindu mythology "Apsara Pramlocha's 907 years romance with Rishi Kandu" as well as other mathematical properties such as being the largest number n so that the imaginary quadratic field Q(√-n) has class number 3. Although I indicated my indifference to numerology, I came across an Numerology article relative to 907. It refers to 16, which is just a sum of 9 & 7, but the article says: "The number 16 is also considered a karmic number, indicating the potential for significant life lessons. These lessons often revolve around the concept of transcendence, teaching individuals that everything in life is transient and subject to change. This realization can lead to profound inner anxiety, making the number 16 challenging to master."
Interestingly, there are 16 fundamental discriminants for class number 3, and of course this is just coincidental.1093 is one of the only 2 known Wieferich primes.
433494437 is 43rd Fibonacci number, and the smallest Fibonacci number equal to the sum of five consecutive primes: 86698853 + 86698867 + 86698883 + 86698901 + 86698933. In addition, 433 is a full reptend prime.
7758337633 is the largest known solution of τ(p)≡0 (mod p) where τ stands for the Ramanujan τ (tau) function. See OEIS A007659. This is a very interesting theme which cannot be overstated. This astounding result was discovered by Nik Lygeros and Olivier Rozier in 2010. Here is an excerpt from the paper in Journal of Integer Sequences.
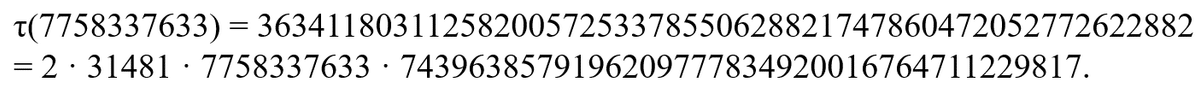
The Ramanujan's constant is a transcendental number using 163 and is important for the theory of class numbers of imaginary quadratic number fields. 163 is so-called 9th member of Heegner numbers = {1, 2, 3, 7, 11, 19, 43, 67, 163}. Here's an excerpt from Wikipedia for Heegner number:
In a 1975 April Fool article in Scientific American magazine, "Mathematical Games" columnist Martin Gardner made the hoax claim that the number was in fact an integer, and that the Indian mathematical genius Srinivasa Ramanujan had predicted it—hence its name. ([Note] Martin Gardner is the author of "The New Ambidextrous Universe: Symmetry and Asymmetry from Mirror Reflections to Superstrings".)

The first Feigenbaum constant δ = 4.669201609102990671853203820466… is so fascinating in terms of connecting the Feigenbaum bifurcation tree and the Mandelbrot set.
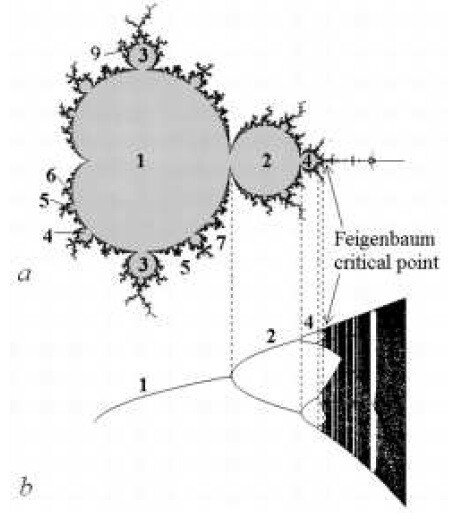
(by Sergey Petrovich Kuznetsov)
P.S. If you are a railfan with some interest in steam locomotives in Japan, you'd love this number. Please be advised that retrieval of its image with showing 9613 numberplate is not easy owing to its strange fate…

■
この記事が気に入ったらサポートをしてみませんか?
