
📏3つの非線形微分方程式 ローレンツのカオス
ローレンツのカオス(Lorenz Chaos)は、気象学者エドワード・ローレンツが1963年に発見した数学的な概念です。これは、予測不可能な振る舞いを示す力学系の一例で、カオス理論の基本的な例として知られています。
ローレンツのカオスは、簡単な3つの非線形微分方程式で表されます。これらの方程式は、大気の対流パターンをモデル化するために開発されました。システムは、初期条件に非常に敏感で、わずかな変化が長期的に全く異なる結果を生み出すことが知られています。これは「バタフライ効果」としても知られており、小さな変化が大きな影響を及ぼすことを意味します。
ローレンツ方程式の解は、時間の経過とともに予測不可能な動きをしますが、特定の制約の中で行われます。この振る舞いは、ローレンツアトラクターと呼ばれる特定の幾何学的形状を形成します。このアトラクターは、カオス的なシステムの典型的な特徴である自己相似な構造を持っています。
ローレンツのカオスは、天気予報の難しさを示す例としてよく引用されますが、カオス理論の研究ではより広い意味を持っています。それは、非常に単純なルールから複雑な動的振る舞いが生じ得ることを示しており、物理学、生物学、経済学、工学など、多くの分野に影響を与えています。

ローレンツアトラクター:
ローレンツアトラクターは、ローレンツ方程式の解が時間の経過とともに進化するときに形成される特定の幾何学的形状です。
このアトラクターは、システムの状態が時間が経つにつれて収束する軌道を示します。これらの軌道はカオス的で、非周期的かつ予測不可能ですが、特定のパターンに収束します。
アトラクターはその複雑さで知られており、カオス理論の典型的な例として引用されます。
ローレンツ方程式は微分方程式の一例です。正確には、ローレンツ方程式は3つの連立した非線形常微分方程式で構成されています。これらの方程式は、力学系の状態変数の時間による変化率を記述します。ローレンツ方程式は以下の形式をとります:
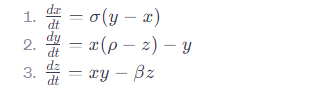
エドワード・ローレンツがローレンツ方程式を通じて行った研究は、気象予報における本質的な限界を理解する上で重要な役割を果たしました。ローレンツの発見は、気象システムが持つ本質的なカオス的特性と、初期条件の微小な変化が長期予報に大きな影響を与える可能性(「バタフライ効果」として知られる)を明らかにしました。
ローレンツは、簡略化された気象モデルを用いてコンピュータシミュレーションを行っていた際に、初期条件のごくわずかな変化が結果に大きく異なる影響を与えることを発見しました。この発見は、天気予報の精度に制限があることを示唆しており、特に長期予報の難しさを説明しています。天気の挙動は非線形的で予測不可能な特性を持ち、そのために長期的な正確な予測は非常に困難です。
この理解は、気象学においてアンサンブル予報の導入につながりました。アンサンブル予報では、異なる初期条件を用いて複数の予報が作成され、それらの結果から予報の不確実性を評価します。これにより、予報の信頼性を高めるとともに、予報の限界をユーザーに伝える手助けとなっています。
ローレンツの研究は、気象予報のみならず、カオス理論と非線形システムに関する広範な分野における理解を進展させました。
第一方程式は、変数 x と y の差に基づいて x の変化率を定義します。ここで、パラメータ σ は変数間の結合の強さを決定します。
第二方程式は、変数 x と z の組み合わせによって y の変化率を定義し、同時に y 自身の値に基づいて減少します。パラメータ ρ はシステムの重要な特性を決定します。
第三方程式は、x と y の積に基づいて z の変化率を定義し、z 自身の値に基づいて減少します。ここで、β は別の重要なパラメータです。
お願い致します
