
上昇流励起を表現するQベクトル天気図
今回はQベクトル の天気図について、この有用性と作図コードについてお話しします。作図する天気図は、高度と温度、Qベクトルの発散、Qベクトルを図示しています。このコードはMetPyを利用しています。記事の最後に、Jupyter Notebook用コードを添付しています。ご利用ください。
今回読み込むデータは、気象庁全球モデル(GSM)のGRIB2形式のファイルです。
Q ベクトルの天気図について
Q ベクトルの収束を確認することで、低気圧や前線、気圧の谷などの影響で上昇流が励起される地域やその強さを把握できます。気象庁数値予報天気図にある700hPa面の上昇流には対流による上昇流も表現されているため、対流の発生や強化に適した総観場かどうかをこの図からは判断できません。対流雲を発生させたり、対流を強める総観場の上昇流励起は、Q ベクトルの収束を確認することで把握できます。Qベクトルが収束し、かつ大気の状態が不安定であるエリアでは対流雲が発生・発達する可能性があります。
Q ベクトルについては、気象庁ホームページにある「総観気象学基礎編」の6.3節に詳しい解説があります。こちらを参考にしてください。
Q ベクトルを計算するために、高度・温度場のスムージング、地衡風の算出が必要になります。MetPyにはさまざまな関数がそろっており、利用するには少々準備が必要ですが、簡単に算出できます。
高度場や温度場のスムージング
データ読み込みからスムージング処理までのコードを下に示します。このスムージング処理では、2つのパラメーター passes と s_n を指定します。passesはスムージング処理の繰り返し回数です。s_n は 5 または 9 のどちらかで、この数の周辺の格子点を使ってスムージング処理します。
最後の2行で、高度場と温度場のスムージング処理を行っています。ここでは、温度場と高度場でのスムージングの処理回数を変えています。
#
import math
import pygrib
import xarray as xr
import matplotlib.pyplot as plt
import matplotlib.ticker as mticker
import numpy as np
import matplotlib.path as mpath
import cartopy.crs as ccrs
import datetime
import sys
#
import metpy.calc as mpcalc
from metpy.units import units
#from scipy.ndimage.filters import maximum_filter, minimum_filter
#
# 作図するGSMの初期時刻を指定する
i_year =2021
i_month = 8
i_day = 23
i_hourZ = 0
#
# 予想時間を与える。この値は注意が必要です。下3桁目が日数、下2桁で時間で与えます。
# 初期値なら0、18時間後なら18、24時間後なら100、36時間後なら112となります。
i_ft = 0
#
# 時間に変換
ft_hours=int(i_ft/100) * 24 + int(i_ft%100)
#
# Q vectorを算出る気圧面を指定
tagHp = 850
#
# 描画する範囲の大まかな指定
i_area = [115, 151, 20, 50] #fx85 日本付近
str_area = "jp" # ファイル名に利用
#
## GPVの切り出し領域の指定:(lonW,latS)-(lonE,latN)の矩形
latS=-20
latN=80
lonW=70
lonE=190
#
## スムージングのためのパラメータ
passes=16 # 高度のスムージングの繰り返し回数
passesT=8 # = passes / 2
s_n = 9 # 9 or 5
#
# データの格納先フォルダー名
##!!! GRIB2データの保存先をFolderを指定すること !!!
data_fld="/Users/hogehoge/Data/gsm/"
####################################################
#
# 読み込むGRIB2形式GSMのファイル名
gsm_fn_t="Z__C_RJTD_{0:4d}{1:02d}{2:02d}{3:02d}0000_GSM_GPV_Rgl_FD{4:04d}_grib2.bin"
gr_fn= gsm_fn_t.format(i_year,i_month,i_day,i_hourZ,i_ft)
#
## データ取得
grbs = pygrib.open(data_fld + gr_fn) # Grib2 Open
#
grbHt = grbs(shortName="gh",typeOfLevel='isobaricInhPa',level=tagHp)[0]
grbWu = grbs(shortName="u",typeOfLevel='isobaricInhPa',level=tagHp)[0]
grbWv = grbs(shortName="v",typeOfLevel='isobaricInhPa',level=tagHp)[0]
grbTm = grbs(shortName="t",typeOfLevel='isobaricInhPa',level=tagHp)[0]
#
# データClose
grbs.close()
#
## データ切り出し
valHt, latHt, lonHt = grbHt.data(lat1=latS,lat2=latN,lon1=lonW,lon2=lonE)
valWu, latWu, lonWu = grbWu.data(lat1=latS,lat2=latN,lon1=lonW,lon2=lonE)
valWv, latWv, lonWv = grbWv.data(lat1=latS,lat2=latN,lon1=lonW,lon2=lonE)
valTm, latTm, lonTm = grbTm.data(lat1=latS,lat2=latN,lon1=lonW,lon2=lonE)
#
## スムージングの実行
# https://unidata.github.io/MetPy/latest/api/generated/metpy.calc.smooth_n_point.html
valHt_sm = mpcalc.smooth_n_point(valHt.squeeze(),s_n,passes) * units("gpm")
valTm_sm = mpcalc.smooth_n_point(valTm.squeeze(),s_n,passesT) * units("K")Q ベクトルとその発散の算出
次に、Q ベクトルの計算に必要な地衡風を算出します。500hPa面天気図作成コードと同様に、MetPyの関数を使うためにxarrayデータセットを作成し、単位も指定しておきます。この準備により、地衡風、Q ベクトル、その発散の算出もとても簡単になります。
## Q vectorなどの算出のためにxarrayデータセットを作成
ds = xr.Dataset(
{
"Geopotential_height": (["lat", "lon"], valHt_sm),
"u_wind": (["lat", "lon"], valWu),
"v_wind": (["lat", "lon"], valWv),
"Temperature": (["lat", "lon"], valTm_sm),
},
coords={
"level": [tagHp],
"lat": latHt[:,0],
"lon": lonHt[0,:],
"time": [grbHt.validDate],
},
)
# 単位も入力する
ds['Geopotential_height'].attrs['units'] = 'm'
ds['u_wind'].attrs['units']='m/s'
ds['v_wind'].attrs['units']='m/s'
ds['Temperature'].attrs['units']='K'
ds['level'].attrs['units'] = 'hPa'
ds['lat'].attrs['units'] = 'degrees_north'
ds['lon'].attrs['units'] = 'degrees_east'
#
# metpy仕様に変換
dsp= ds.metpy.parse_cf()
#
# 地衡風計算 平均処理した高度から求める
dsp['ug'], dsp['vg']= mpcalc.geostrophic_wind(dsp['Geopotential_height'])
#
## Q vector計算
dsp['u_qv'], dsp['v_qv'] = mpcalc.q_vector(dsp['ug'], dsp['vg'],
dsp['Temperature'],
tagHp * units.hPa)
#
## 発散計算
dsp['q_div'] = mpcalc.divergence(dsp['u_qv'],dsp['v_qv'])天気図への描画
次のコードでは、表示する時刻の文字列を取得し、描画する等値線などを指定し、後半部分で作図の準備、海岸線と緯線・経線を描画します。
#### 作図用処理
## 年月日
dt_v = grbHt.validDate
dt_i = grbHt.analDate
dt_str = (dt_i.strftime("%H00UTC%d%b%Y")).upper()
dt_str2 = dt_i.strftime("%Y%m%d%H")
#
# Q vectorの発散のハッチの指定
clevs_qdiv = list(range(-30, -4, 5))+list(range(-2,3,4))+list(range(5, 31, 5))
# 温度の等値線の指定
clevs_tmpc = np.arange(-39, 42, 3)
# 高度の等値線の指定
clevs_hght = np.arange(0, 8000, 30)
#
# 緯線・経線の指定
dlon,dlat=10,10 # 10度ごとに
#
#
## 図法指定
proj = ccrs.Stereographic(central_latitude=60, central_longitude=140)
latlon_proj = ccrs.PlateCarree()
## 図のSIZE指定inch
fig = plt.figure(figsize=(10,8))
## 余白設定
plt.subplots_adjust(left=0, right=1, bottom=0.06, top=0.98)
## 作図
ax = fig.add_subplot(1, 1, 1, projection=proj)
ax.set_extent(i_area, latlon_proj)
#
## 海岸線
ax.coastlines(resolution='50m',)
## グリッド線
xticks=np.arange(0,360.1,dlon)
yticks=np.arange(-90,90.1,dlat)
gl = ax.gridlines(crs=ccrs.PlateCarree()
, draw_labels=False
, linewidth=1, alpha=0.8)
gl.xlocator = mticker.FixedLocator(xticks)
gl.ylocator = mticker.FixedLocator(yticks)Q ベクトルの発散をシェードで表現するために、ax.contourf()関数を用い、カラーテーブルを cmap=plt.cm.bwr_r と指定しています。デフォルトで用意されているカラーテーブルは、ここから確認してみてください。このテーブル名の末尾に"_r"を加えると、カラーテーブルの大小の色を反転させることができます。
温度表示のために単位をKelvinからCelsiusに変換する必要があります。次のように、簡単に変換することができます。
dsp['Temperature'] =
(dsp['Temperature']).metpy.convert_units(units.degC)
Q ベクトルの矢印描画については、wind_slice を使って風のデータを間引き指定を行い、ax.quiver()を使って矢印を表示しています。また、凡例はax.quiverkey()により描画できます。
## Plot Q-Vector Divergence and scale
cf = ax.contourf(dsp['lon'], dsp['lat'], dsp['q_div']*1e18, clevs_qdiv,
cmap=plt.cm.bwr_r,
extend='both', transform=latlon_proj)
ax_reld = fig.add_axes([0.1, 0.1, 0.8, 0.02])
cb = plt.colorbar(cf, orientation='horizontal',
shrink=0.74, aspect=40, pad=0.01, cax=ax_reld,
ticks=clevs_qdiv)
cb.set_label('Q-Vector Div. (*10$^{18}$ m s$^{-1}$ kg$^{-1}$)')
#
## Plot Temperatures
# K=>Celsius
dsp['Temperature'] = (dsp['Temperature']).metpy.convert_units(units.degC)
cn_tmp = ax.contour(dsp['lon'], dsp['lat'], dsp['Temperature'],
colors='gray', alpha=0.6, linestyles='dashed',
linewidths=1.2, levels=clevs_tmpc, transform=latlon_proj )
ax.clabel(cn_tmp, clevs_tmpc, fontsize=15, inline=True, inline_spacing=5,
fmt='%i', rightside_up=True)
#
## Plot Geopotential Heights
cs = ax.contour(dsp['lon'], dsp['lat'], dsp['Geopotential_height'], clevs_hght, colors='black',
transform=latlon_proj)
plt.clabel(cs, fmt='%d')
#
## Plot Q-vectors, scale to get nice sized arrows
wind_slice = (slice(None, None, 3), slice(None, None, 3))
q = ax.quiver(ds2['lon'][wind_slice[0]], ds2['lat'][wind_slice[1]],
ds2['u_qv'].values[wind_slice], ds2['v_qv'].values[wind_slice],
pivot='mid', color='black',
scale=1e-11, scale_units='inches',
transform=latlon_proj) # scale_units='inches'
# 凡例表示
ax.quiverkey(q, X=0.82, Y=-0.016, U=1e-11, label='1*10$^{-11}$ m$^{2}$ kg s$^{-1}$', labelpos='E',
fontproperties={'size': 11})
#
## Caption
fig.text(0.5,0.01,"GSM FT{0:d} IT:".format(ft_hours)+dt_str+
" {0}hPa Heights, Temp, Q-Vector, Q-Vector Div".format(tagHp) ,
ha='center',va='bottom', size=15)
plt.show()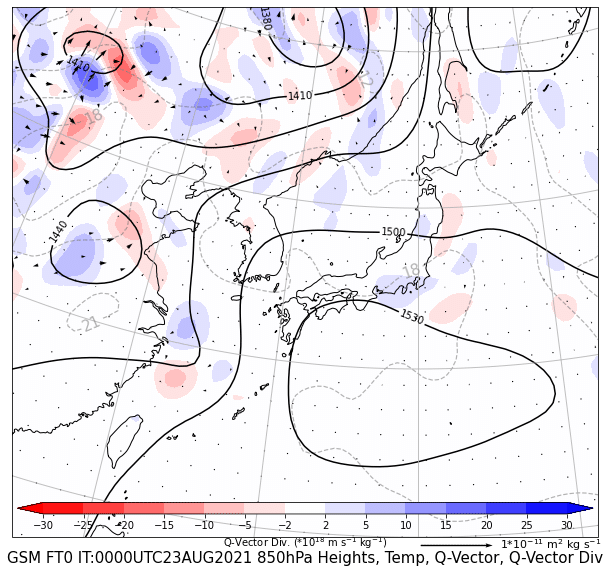
サンプルコード
最後に、上に図示した850hPa面のQベクトル天気図を作成するコード(Jupyter notebook用)を掲載します。ご利用ください。
次回は、ジェット気流の解析に適した数値予報天気図について説明していきます。
