マクローリン展開の詳細（「オイラーの等式の説明」補足記事）

説明に必要な収束値

本記事では累乗/階乗の収束値が必要となる。

この収束の証明は、本記事の主目的から離れるので、後述する。​

マクローリン展開の適用条件

f(x)をマクローリン展開してn次多項式で表現するためには、以下の条件を満たす必要がある。
(1)f(x)が-∞〜∞の範囲で、無限回微分できる
(2)テイラーの定理の剰余項がn→∞で0に収束する
テイラーの定理の剰余項は以下のものである。（詳細は後述のテイラーの定理）

厳密に言うとさらに
(3)関数f(x)が定義域-∞〜∞で一様収束する
言い換えると
「関数f(x)の収束半径が∞である」
ことも条件である。
その判定法はともかく、なぜその条件が必要なのかまで記述するには筆者の能力が足りない。
本記事の目的である、オイラーの公式の構成要素がマクローリン展開可能であることを示すには、上記の(1)(2)で充分なので、その説明に留めておく。
（実際、いずれも収束半径は∞になることが分かっている）

オイラーの公式を構成する、3つの関数について、この条件を満たすことを示す。

(1) 無限回微分できる
      ∵ 何度微分しても同じである

(2) 0に収束する

［sinθ］

(1) 無限回微分できる
      ∵ sinθ → cosθ → -sinθ → -cosθ → sinθ
          と、4回微分すると元に戻る

(2) 0に収束する

［cosθ］

(1) 無限回微分できる
      ∵ cosθ → -sinθ → -cosθ → sinθ → cosθ
          と、4回微分すると元に戻る

(2) 0に収束する

マクローリン展開の証明

マクローリン展開

はテイラー展開

の一種（a=0としたもの）である。
テイラー展開はテイラーの定理に基づく。（剰余項を無視した形のもの）
［テイラーの定理］

テイラーの定理の証明には、以下の段階すを踏む必要がある。

以下、順番にそれぞれの証明を記述する。

［ロルの定理］

閉区間 [a,b]で連続でかつ開区間 (a,b)で微分可能である関数 f(x)に対して，等式
    f(a)=f(b)
が成り立つならば
    f′(c)=0，a<c<b
を満たす実数cが存在する。

なお、
    閉区間 [a,b] 両端点を含む区間         a≦x≦b
    開区間 (a,b) 両端点を含まない区間 a<x<b
を意味する。

有界閉区間上の連続関数は最大値および最小値を持つことの証明は、本記事の範囲を超える（実数の公理にまで遡る必要がある）ため省略する。
これは
「ある範囲で連続な関数には最大値および最小値がある」
と言い換えると、常識的に納得できるであろう。

［コーシーの平均値定理］

閉区間 [a,b]で連続、開区間 (a,b)で微分可能な
f(x),g(x)に関して、
g(b)−g(a)≠0ならば、　

を満たす変数cが存在する。（ただし、 g′(c)≠0）

［テイラーの定理］

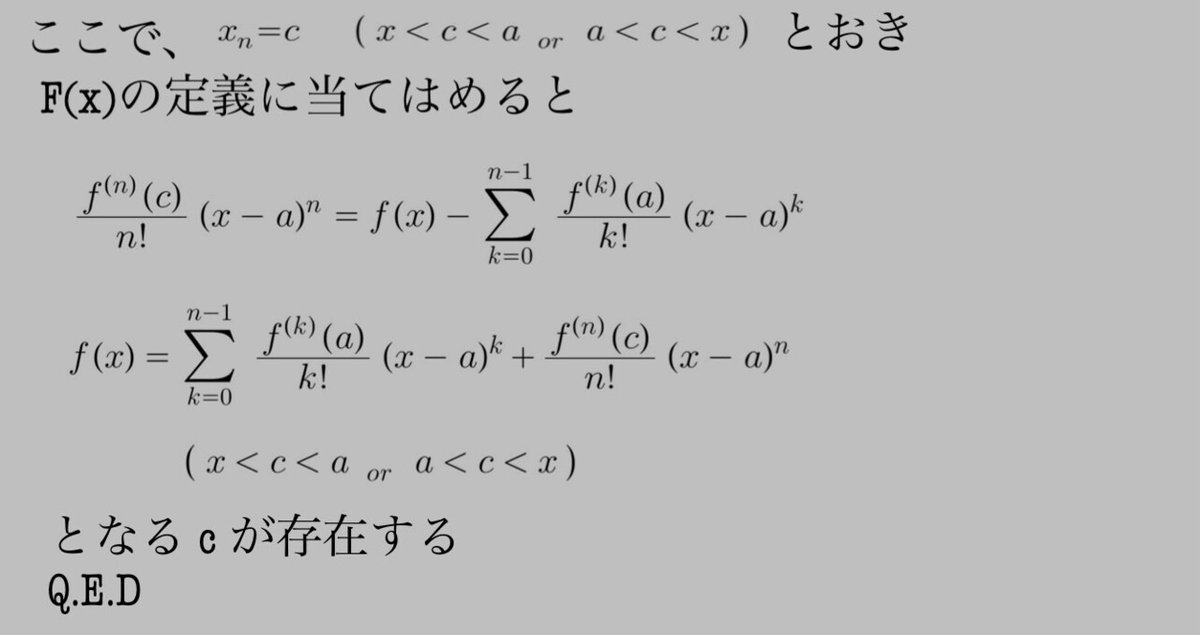
累乗/階乗の収束（補足の補足）

以上.