
「フェルマーの最終定理」を証明した数学者ワイルズ
こんにちは^^
先日に【世界一やさしい「やりたいこと」の見つけ方】を読んで、自分が本当に「大事なこと(価値観)」とは何か?、これから見つけていこうと思ったので、少しずつ記事にしていければと思います。(以下の記事参照)
今回は、わたしが数年前テレビ(もしくはYoutube?)で知った、アンドリュー・ワイルズというイギリスの数学者の話です。わたしは当時、この数学者のエピソードを知って、心に響いたことがあって、それが今でも記憶に残っています。「大事なこと」を見つけるときには、尊敬する人やキャラクターの尊敬するところやエピソードの中に潜んでいることが多いそうですので、そのエピソードを掘り出してみます。
「フェルマーの最終定理とは」
ワイルズという人は、「フェルマーの最終定理」を解いた人ですが、この「フェルマーの最終定理」というのは、
3以上の自然数 n に対して、
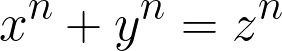
を満たす自然数(x, y, z)の組み合わせは存在しない
というものです。このことを証明するために、ガウスやオイラーといった名だたる数学者が挑んでも解くことができず、300年以上もの間ずっと誰も証明ができていませんでした。ワイルズはその証明を行なうことができた人物です。といっても、その証明を行なうことは決して容易なものではなく、長い時間がかかりました。
ワイルズの生い立ち
ワイルズは小さい頃からとても優秀で、数学が大好きな少年でした。10歳の時、図書館に行ったときに、ワイルズは「フェルマーの最終定理」に出会いました。そこで、その数式が300年間以上解かれなかったことを知って、
「その瞬間、私は絶対にこの問題を放置するまい、これを解かねばならないと思った」
そうです。
そしてその後彼は、数学を専攻することを志し、大学・大学院まで進学していきました。しかし、彼が大学院の研究テーマとして、「フェルマーの最終定理」の証明に取り組もうとしたら、当時の指導教授から辞めるように助言されたそうです。
当時の教授は、様々な数学者が長い間挑んでも解くことができなかったことから、ワイルズがいかに優秀であっても、なかなか証明することができないだろうと心配していました。それよりも、他のテーマに取り組んだ方が確実に成果を出すことができるだろうと、信じていました。
ワイルズはこの指導教授の助言を受け入れることにして、「フェルマーの最終定理」の証明に取り組むことを諦め、「楕円曲線」を研究することにしました。
また、大学院を修了し、博士号を取得して助教授となった後は、「楕円曲線」とは異なる分野の「モジュラー形式」についても研究するようになりました。(※「楕円曲線」と「モジュラー形式」は著者のわたしもわかっていませんので、そういう数学の分野があるのだと思ってお楽しみください)
とうとう「フェルマーの最終定理」の証明に挑む
「楕円曲線」と「モジュラー形式」について研究し、著名な功績を出して大学の教授となった後も、「フェルマーの最終定理」について証明に取り組もうとはしませんでした。
しかし、転機が訪れました。
1986年のある日、ケン・リベットというアメリカの数学者が
【フライの楕円曲線は「モジュラー」ではない】
ということを証明しました。
「フライの楕円曲線」とは、以下のようなもので、
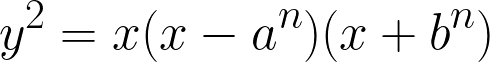
フェルマーの最終定理に対する反例となる(らしい)のですが、これがフェルマーの最終定理の証明へと導く大きな転換点となったのです。
どういうことかというと、当時まだ証明されていなかった、ある一つの予想があるのですが、この予想を証明すると、フェルマーの最終定理を証明することにもなるのです。その予想とは、
【すべての有理数体上に定義された楕円曲線は「モジュラー」である】
という谷山-志村予想であり、谷山-志村予想を使って、背理法からフェルマーの最終定理を導くことが以下のようにできます。
(1) 「フェルマーの最終定理」について、3以上の自然数 n の場合において、自然数(x, y, z)の組み合わせが存在するとする。(「フェルマーの最終定理」は「偽」と仮定)
(2) この自然数の組み合わせから、楕円曲線を作ることができる。(フライの楕円曲線)
(3) フライの楕円曲線は「モジュラー」ではない。⇒ ケン・リベットが証明。
(4) 谷山-志村予想が正しいのならば、楕円曲線は全て「モジュラー」であるはずだから、「モジュラー」ではない楕円曲線は存在しないはず。
(5) (4)より、「モジュラー」ではないフライの楕円曲線は存在しないはずなので、(1)の仮定が誤っていることになる。(「偽」ではない。)
(6) 以上より、「フェルマーの最終定理」は「真」となり、証明したことになる。
そういうわけで、上記(4)の「谷山-志村予想が正しい」ということを、ワイルズが証明できれば、「フェルマーの最終定理」を証明できたことにも繋がります。ワイルズは「楕円曲線」と「モジュラー」を研究していたので、まさに運命の巡り合わせでした。
転機が訪れてから、ワイルズは「フェルマーの最終定理」の証明に本格的に挑むようになりました。彼はずっと一人で証明に挑んだものの簡単にはいかず、7年かけてやっと証明が終わりました。
そして、彼は1993年に大学の講義で3日間かけて「フェルマーの最終定理」の証明を発表しました。発表が終わった時、講義に参加していた何名もの数学関係者から称賛されたそうです。
致命的な誤り発見!それでも・・・
ここでやっと終わると思いきや、証明を数学の論文誌に投稿したあと、致命的な誤りが一つ発見されてしまいました。そのままだと、「フェルマーの最終定理」が証明したことになりませんでした。
そこで、ワイルズは、彼の弟子であるリチャード・テイラーも加えて一緒に、証明の誤りの修正に取り組みました。しかし、1年ほど修正に取り組んでも修正方法が見つからず、ワイルズは諦めかけました。ですが、弟子のテイラーの励ましもあって、なんとか諦めずに証明に挑み続けました。
すると、1994年9月19日、突然インスピレーションが湧いて、「夢じゃないかと思うような素晴らしい証明」が頭に浮かび、修正して、証明が完成したそうです。
完成した論文は1995年に掲載され、査読の結果、無事「フェルマーの最終定理」が証明されたことが認められたそうです。
※数学者アンドリュー・ワイルズのエピソードについては以下のブログ、動画、wikipediaを参考にしており、もっと詳しい内容を知ることができると思います。興味がありましたら見てみてくださいm(_ _)m
数学者ワイルズのエピソードから知ったわたしの「大事なこと」
わたしは数年前にワイルズのエピソードを知って、心に響いたことを覚えています。そして、それは今もずっと心の中にあります。ワイルズのエピソードから、わたしが心に響いたポイントは以下の通りです。
①ワイルズが10歳のとき、図書館で「フェルマーの最終定理」と出会って、
「その瞬間、私は絶対にこの問題を放置するまい、これを解かねばならないと思った」こと。
②ワイルズが大学院のテーマで「フェルマーの最終定理」の証明に取り組もうとしたとき、指導教授の助言を受け入れ、一旦諦めた。けれども、その後に研究した別のテーマの「楕円曲線」と「モジュラー」が結果的に「フェルマーの最終定理」を解くため突破口となったこと。
③1人で7年もの長い間証明に挑み続けたことと、その後誤りが見つかって1年もの修正に取り組み続けることになっても諦めなかったこと。
①では、小さい頃に思ったことが、大人になって達成できたことが素直に凄いと思いました。②では、一旦諦めて別の分野を研究したことが結果的には目標を達成するための近道となっていて、人生って不思議なこともあるのだなと感じました。
さらに、③については、最も心に響いていて、証明に7年、修正に1年かかっていましたが、いったいどれだけの時間、「その数式を証明するため」に葛藤し続けていたのだろうと思いました。想像しても、なかなか理解することは難しくて、きっと本人にしかわからないような苦難があったのだろうなと思いました。
もしかしたら、楽しんでいた時もあったのかもしれないし、ワクワクしていたのかもしれません。だとしても、この長い時間挑み続けられるところが最も尊敬できるところだと思います。
もし、上記のポイント①~③が、わたしの「大事なこと」に関連しているならば、
「継続」「挑戦」「不屈」「信念」…
といったキーワードがわたしの「大事なこと」として含まれているのだろうなと思います。
おわりに
長くなりましたが、ここまで読んでくださってありがとうございました。今回は数学者のアンドリュー・ワイルズのエピソードに触れて、わたしの「大事なこと」を分析してみましたが、まだまだ他にも「大事なこと」はあると思いますので、また他にも「大事なこと」を探してみて、面白そうなものがありましたら、記事にしてみます。
この記事が気に入ったらサポートをしてみませんか?
