
1-2. 金属結晶の構造
こんにちは。おのれーです。絵を描くのが苦手なため、更新に時間がかかってしまいました…。
前回、「固体」はそれを構成する原子やイオン、分子などの粒子が、粒子間の引力によって、一定の位置に固定されているものであり、その中でも粒子が規則正しく配列してできたものを「結晶」ということを確認しました。
今回からは、具体的に結晶にはどのような種類があり、どのような構造をしているのかということを見ていきたいと思います。
第一弾は金属結晶についてです。
なお、金属結晶がどのようにできるかは"化学基礎"で学んでいますので、もう一度確認したい方は下の記事をご覧ください。
では、始めます。
■金属結晶の単位格子
金属結晶は、たくさんの金属元素の原子同士が、金属結合で結びついてできています。例えば「銅」という金属であれば、銅原子という原子が、規則正しく結びついてできています。

このとき、金属の原子が結びつく規則には種類がいくつかあり、それぞれ異なる結晶格子(粒子がどのように集まっているかを示したもの)で表されます。
代表的なものは、体心立方格子、面心立方格子、六方最密構造とよばれるものです。下に、その最小の繰り返し単位である単位格子を示しておきます。

これらの単位格子に含まれる原子の数はそれぞれ決まっています。さらに、結晶において、1個の原子に隣接する原子の数を配位数といい、こちらも結晶格子の種類によって決まっています。
まずこのあたりのことに注目をして、3種類の結晶格子を見てみましょう。
◎体心立方格子
リチウムLi、ナトリウムNa、カリウムKなどの金属は、体心立方格子の構造をとることが知られています。
体心立方格子は、下図に示すように、立方体の中心に原子が1個ドカンと居座っています。なので、「立方体の中心に原子が存在する」=「体心立方格子」と覚えるとよいでしょう。

単位格子内には、中央にある1個のほか、立方体の頂点それぞれに1/8個分の原子が存在しており、合計2個の原子が含まれています。
さらに、中心の原子に注目をすると、1個の原子が、立方体の頂点にある8個の原子と隣接しているので、配位数は8です。

ちなみに、頂点にある原子が1/8個分であることは、実際にリンゴやスイカなど、球状の果物を包丁で切っていくと、実感することができるので、ぜひ試してみてください(今回はミニトマトでやってみました。写真撮影後は美味しくいただきました!)。

◎面心立方格子
銅Cu、銀Ag、アルミニウムAlなどの金属は、面心立方格子の構造をとることが知られています。
面心立方格子は、下図に示すように、立方体の各面の中心に原子が存在しています。なので、「立方体各面の中心に原子が存在する」=「面心立方格子」と覚えるとよいでしょう。

単位格子内には、立方体の各面に1/2個分の原子が存在しているほか、立方体の頂点それぞれに1/8個分の原子が存在しており、合計4個の原子が含まれています。
配位数を考えるときには、下図のように単位格子を2つ並べて考えます。2つの単位格子の境目にある中心の原子に注目をすると、12個の原子と隣接しているので、配位数は12です。

◎六方最密構造
ベリリウムBe、マグネシウムMg、亜鉛Znなどの金属は、六方最密構造の構造をとることが知られています。
六方最密構造の単位格子は、下図のような正六角柱の六方最密構造の1/3にあたります。
六方最密構造の正六角柱には、側面に1個分の原子が3個、頂点に1/6個分の原子が12個、上下面に1/2個分の原子が2個の原子が存在しており、合計6個の原子が含まれています。しかし、単位格子はこの1/3の部分ですので、単位格子中の原子数は、6÷3で2個になります。

配位数を考えるときには、下図のように正六角柱を2つ並べて考えます。2つの単位格子の境目にある中心の原子に注目をすると、12個の原子と隣接しているので、配位数は12です。

■単位格子の一辺の長さと原子半径
結晶の単位格子の一辺の長さが分かれば、原子の半径を求めることができます。ここでは実際に、体心立方格子と面心立方格子の原子半径を求めてみましょう。
◎体心立方格子
単位格子一辺の長さをl 、原子半径をr として、立方体を対角線で切断した面に注目してみます。

図を見ても分かるように、切断面の長方形の対角線は、原子の半径4つ分、つまり4r で表すことができます。長方形の縦の長さはl 、横の長さは√2 l と分かっていますので、三平方の定理から、原子半径r の大きさをl を使って表すと、以下のように整理することができます。

また、単位格子の体積(立方体の体積)のうち、原子がどのくらいの体積を示すのかを表した割合を充填率と呼んでいます。体心立方格子の場合は、下式で求められるように、68 %です。

◎面心立方格子
単位格子一辺の長さをl 、原子半径をr として、立方体の1つの面に注目してみます。

図を見ても分かるように、立方体の一つの面に相当する正方形の対角線は、原子の半径4つ分、つまり4r で表すことができます。正方形の一辺の長さはl と分かっていますので、三平方の定理から、原子半径r の大きさをl を使って表すと、以下のように整理することができます。
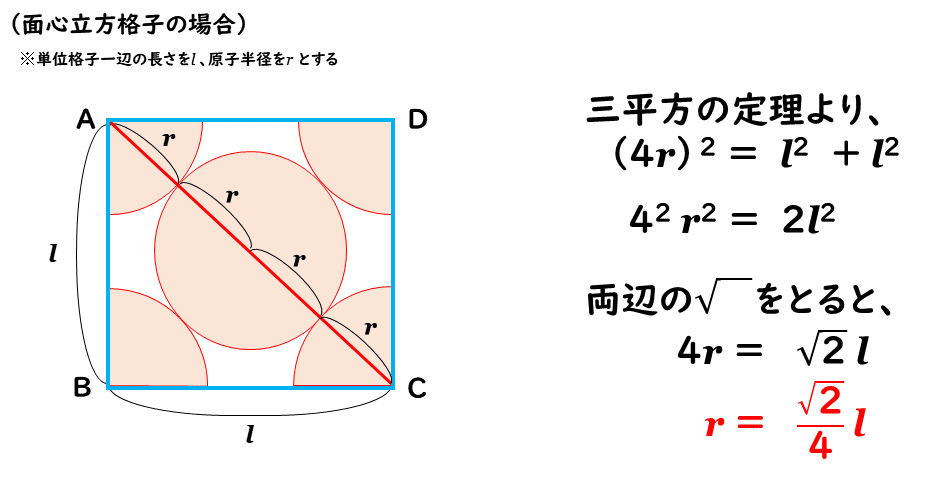
また、面心立方格子の充填率は、下式で求められるように、74%です。体心立方格子よりも原子が密につまっている状態にあることがわかります。

ではここで、問題を一つ解いてみましょう。

■結晶の密度と原子量
ここまででも少し計算が大変になってきたかなと思うのですが、もう少しだけ頑張って、最後に密度について考えてみたいと思います。
そもそも、密度とはいったい何だったでしょうか?
密度: 物質の単位体積あたりの質量のこと
言い換えると、同じ体積の物体を持ってきたとき、質量を比べるとどうなるかを表したのが密度です。一般に、固体の密度は物体1 cm3あたりの質量[g]で表し、単位は[g/cm3]で表します。
密度は、物質の種類ごとに決まっているので、密度を測定することで、その物体が何で出来ているのかを特定したり、結晶に不純物がどのくらい含まれているのかを調べたりすることができます。
では、結晶の構造から密度を求めるためには、どうすればよいのでしょうか?
・・・実は、結晶を作っている原子の原子量が分かれば、密度を求めることができます。
原子量(原子1 molあたりの質量[g]に等しい)をM、アボガドロ定数をNA [/mol]とすると、原子1個の質量は次のように求められます。
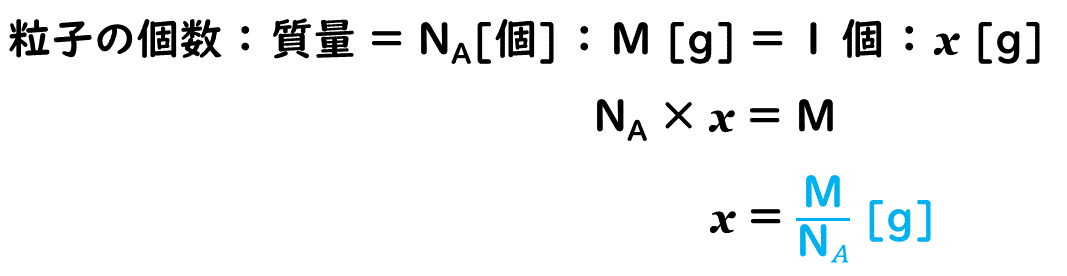
したがって、単位格子中の原子の数をnとすると、単位格子1個あたりの質量は次のように表すことができます。

また、単位格子1辺の長さをl [cm]とすると、単位格子1個の体積はl^3 [cm3] となります。
したがって、結晶の密度は次のように求めることができます。

では、ここで一つ問題を解いてみましょう。
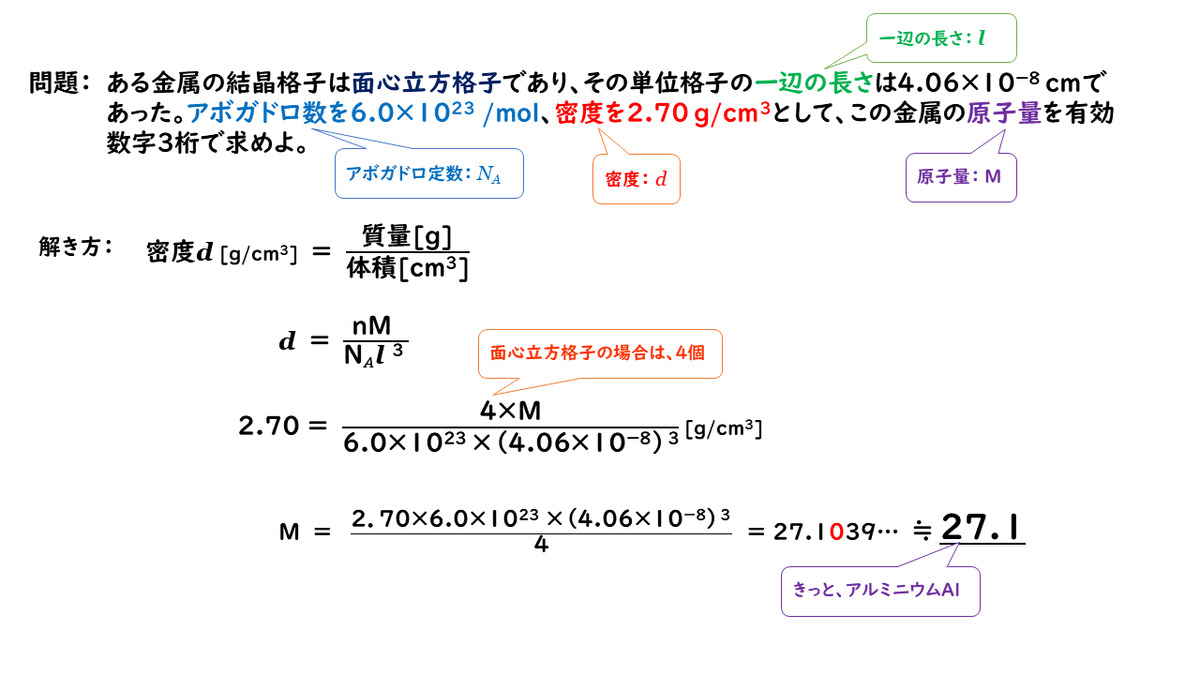
少し盛りだくさんになってしまいましたが、今日はここまでです。
結晶の基本的な性質は、その結晶構造によって決まります。したがって、結晶の構造を知ることは、その性質を研究するために重要であるばかりでなく、必要とする性質をもった物質を合成するための指針にもなることがあります。
この100年の間、X線結晶学が発展して、多くの結晶の構造が明らかにされてきました。しかし、結晶の形態については今だ未知の部分が多いのが現状です。
つい計算ばかりに目が向きがちな分野でもありますが、何のための計算なのかというところを大切にして学びを深めていけたらなと思います。
最後にワンポイントチェック
1.金属結晶の結晶格子を3種類あげなさい。
2.それぞれの結晶格子に含まれる原子数は何個か。
3.それぞれの結晶格子に含まれる配位数はいくつか。
4.原子半径を求めることができるか。
5.充填率を求めることができるか。
6.単位格子の構造から、結晶の密度を求めることができるか。
