空気抵抗についての研究
この記事は私が今研究している球にかかる空気抵抗に関する研究を簡単にまとめたものです。研究といっても専門機関や大学などでやっているわけではなく、ただ物理学が好きな高校生が趣味(部活)の一環としてやっているものなので、内容は稚拙だと思います。ぜひアドバイスをしていただいたり、温かい目で見ていただけると幸いです。
さて、この研究は「球体における空気抵抗係数について」という題名ですが、主に考察しているのは主に、空気抵抗はどんな物理量とどんな関係があるのか、ということだけです。細かく分けると、速度や球体の半径にどのように関わるのかということを調べています。球体にかかる空気抵抗を調べることで、日常の物体の運動を完全に予測できる、というのが大きなモチベーションです。理論と実験に大きく分かれていますが、まずは理論から説明します。
【理論】
まず、空気抵抗力Dは他の物理量のどんな関数になっているかというのを考察していきます。空気などに代表されるニュートン流体(流れの剪断応力と速度勾配が比例する流体)の運動は、以下のNavier–Stokes方程式によって完全に記述されます。ただし、粘性率は一定で、非圧縮性流れを仮定します。

また、落下させる球体の性質(具体的には半径と質量)と連続の方程式によって空気抵抗力を記述できるはずです。これは物体の半径や速さが小さいときには解析的に解くことができますが、日常で目にする大きな球に対しては解析的に解くことができません。よって、次元解析によって関数形を決定します。
先ほど述べたように空気抵抗力は上の式から記述されるはずです。具体的には、空気と物体の相対速度、空気の密度、粘性係数、圧力、温度、重力加速度、半径、質量、などが挙げられます。速度、粘性係数、半径は直感的にも抵抗力に関与することがわかります。重力加速度は水平方向と鉛直方向の抵抗力に差がないことを示すことで関与しないことがわかりますが、私はまだここに上手い理論的説明をすることができていません。また、なぜ質量が関与しないかもまだ説明ができていません。また、圧力と温度についてはその影響を全て密度に押し込むことで表現できるでしょう。
以上より、抵抗力Dは粘性係数η、空気の密度ρ、球体と空気の相対速度v、球体の半径rに関係すると考えられます。したがって、次元解析により抵抗力Dは以下のようになります。[1]
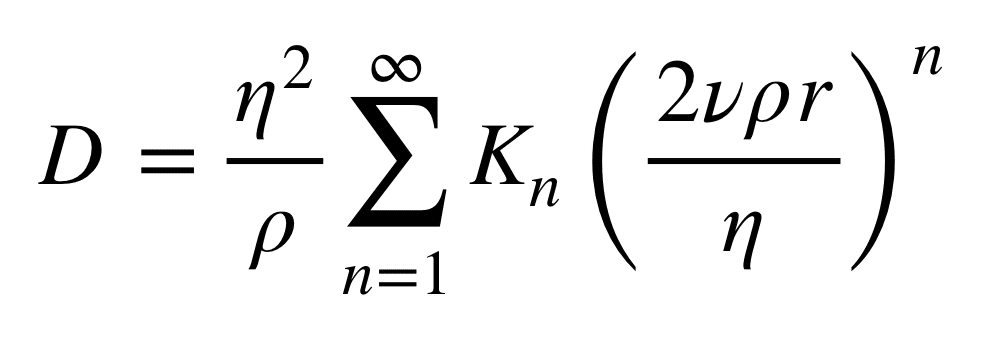
ここでKは定数です。この式からわかるのは例えば速度と半径は同じ指数を持つ、とかです。のちに重要な考察になります。この式にはシグマやらいろいろ入っていて見にくいので抗力係数と呼ばれる量を用いて以下のように書き直しましょう。(抗力係数C_Dはη,ρ,v,rの関数です。)

この式を(1)とします。これはさっきにの式でn=2以外の項を全て抗力係数に押し込んで表現しています。(これをC_D=の式に直すと分母にはエネルギーが現れたりして都合のいい感じになっているのです。)
一般に、抗力係数はレイノルズ数Reと呼ばれる無次元量の関数になっています。

このレイノルズ数と抗力係数の関係を示したグラフはこんな感じです。[2] これも実験的に求められているそうです。

これを見るとRe≈10^4付近ではC_Dはおおよそ一定値を示していることがわかると思います。(1)においてC_Dが定数であるというのはすなわち抵抗力が速度の2乗に比例しているということです。この仮定を後の実験で使います。
【実験理論】
いよいよ実験に入りますが、もう少しだけ理論を使います。
先の理論より、ある程度大きい球体は抵抗係数が定数となり、空気抵抗力が球体の速度の2乗に比例するようになると仮定します。この実験では、以下に定義する空気抵抗係数kが、半径とどのような関係にあるのかを調べます。

つまり、(1)において速度^2の係数をkとした感じです。
さて、半径r,質量mの球を時刻t=0で落下させたとき、時刻tでの球の速度をv(t)とします。このとき、Newtonの運動方程式は

となります。ただし浮力の影響は質量mに押し込むことで考慮されます。この微分方程式を解くと、

が得られます。ただし、v(t)=0としました。これをt=0からt=tまで時間で積分することによって球の落下距離hが得られるはずです。積分を実行すると

を得ます。準備が整いました。この式を(2)とします。
【実験】
実験に使用したもの
・iPhone7 (240fpsで撮影可能)
・パーソナルコンピューター
・電子天秤
実験方法 高さ1.70mから質量と関係が異なる発泡スチロール球X=A,B,C,D,Eを落下させ、その様子をカメラで撮影しました。(誤差についてはあとで記述します)その映像をパソコンに取り込んでコマ数を数え、落下にかかった時間t_Xを計測しました。また、各発泡スチロール球についてそれぞれ質量m_Xを測定しました。
データの解析 t=t_X , m=m_X , h=1.70 を式(2)に代入し、数値計算(二分法)によって解k=k_Xを計算しました。
仮説 各発泡スチロール球についてレイノルズ数を計算するとだいたい10^4程度になるから、先の理論より、抵抗係数はおおよそ一定値なのだから、空気抵抗係数は半径の2乗に比例すると考えられます。
実験結果

結果をまとめたものが上の表です。また、各球について、発泡スチロール球と半径の両対数グラフを示します。

ただし、直線は最小二乗法によって引いてあります。エラーバーはのちに考える誤差(誤差の最大値)を考慮して書いてあります。
考察
(追記予定)
映像撮影日 2019 8/5 気温35.5℃ 1008hPa 蒸気圧25.4hPa 湿度44%
参考文献
[1]伊東敏雄, “な〜るほどの力学,“ 学術図書出版, 1994
今井功 ,”流体力学 (前編),” 裳華房, 1973
[2]Faith A. Morrison, “Data Correlation for Drag Coefficient for Sphere,” Department of Chemical Engineering, Michigan Technological University, Houghton, MI, 2016
Phillip P. Brown, Desmond F. Lawler, “
Sphere Drag and Settling Velocity Revisited,” Journal of Environmental Engineering 129(3), 2003
J. M. Cimbala, “Drag on Spheres,” Penn State University, 2012
計算について気になる人はこちらをどうぞ
この記事が気に入ったらサポートをしてみませんか?
