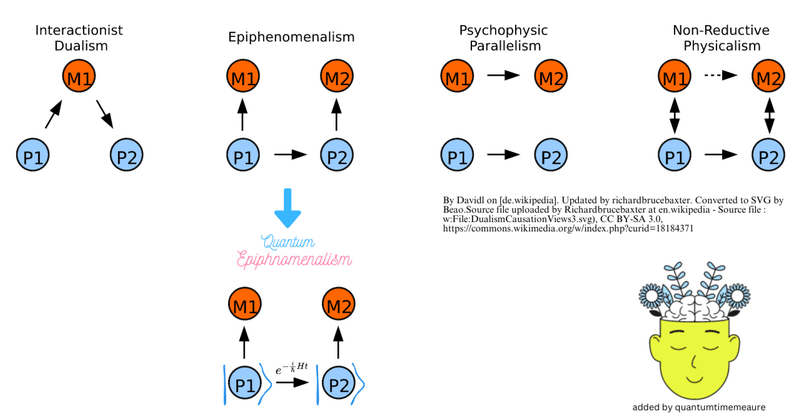
量子論的随伴現象説（Quantum Epiphenomenalism）

本稿は、心の哲学における一説である随伴現象説を、できるだけ単純な方法で量子論に拡張することを試みるものである。数式が多いが、哲学であるので、物理学のように数式を展開（計算）して何かを求めるとか、数学のように何かを証明するようなことはない。哲学なので、筆者には特に奇異ではなく（ありえるだろう）と思われることをそれほどの根拠なく述べるものである。筆者としては、将来的に随伴現象説が量子論における射影仮説を代替し、観測問題に心を惑わされることなく過ごせるようになることを期待して本稿を執筆するものである。

通常の（量子論でない）随伴現象説

一人の場合

随伴現象説によれば、意識やクオリアは物質の物理的状態に付随している現象である。すなわち、物理量の組み$${\{P_i\}}$$からメンタルな状態$${M}$$への写像$${S}$$が非物理的な意味で存在するというのが随伴現象説である。
すなわち、

$$
S: \{P_i\} \mapsto M
$$

である。あるいは、物理量を定義域、メンタルな状態を値域とする関数$${f_S}$$を用いて、

$$
f_S(\{P_i\} ) = M
$$

と書いた方がわかりやすいかもしれない（あまり一般的ではないが、関数は$${f}$$と書いた方が見慣れている方が多いと思われることから関数と表現する場合は写像の記号を$${f}$$の添字につけて表すことにする。）。

上の方で、「メンタルな状態$${M}$$への写像$${S}$$が非物理的な意味で存在する」と書いたが、いろいろな意味での存在があり、ここでは、「古典物理学的（非量子論的）に存在」、「量子物理学的に存在」、「非物理的に存在」の3種類を区別しておきたい。本稿では、古典物理学的（非量子論的）に存在することを実在すると呼ぶことにしたい。すなわち、$${P_i}$$は実在し、メンタルな状態$${M}$$と写像$${S}$$（あるいは関数$${f_S}$$）は実在しない。しかし、$${M}$$と$${S}$$は非物理的な意味で存在している。

$${M}$$と$${S}$$が存在しているというのは、随伴現象説で考えるということの言い換えであり、そこに万人を納得させられそうな根拠はない。他の説に比べれば随伴現象説は問題が少ないので採用する程度の理由である。「量子物理学的に存在」とは、量子力学における状態（ヒルベルト空間の元）として存在するという意味である。量子力学における状態（ヒルベルト空間の元）は、古典物理学的（非量子論的）に実在しているわけではないが、本稿ではなんらかの意味で存在している（メンタルな状態よりは物理的な意味で存在している）と考えられる。メンタルな状態やメンタルな状態への写像を存在すると言うのであれば、量子力学における状態（ヒルベルト空間の元）も存在すると言っても良いだろう。

二人の場合

私（アリス）の意識$${M_a}$$とある他人（ボブ）の意識$${M_b}$$は、当然であるが、異なる物量の組み（異なる位置にある脳内の電位等）$${\{P_i\}}$$と$${\{P_j\}}$$にそれぞれ随伴している。
すなわち、

$$
f_S(\{P_i\} ) = M_a , \\
f_S(\{P_j\} ) = M_b
$$

である。アリスとボブの物理量からメンタルな状態への写像は同じである必要はない（同じという根拠はない）が、本稿では記号をシンプルにするために同じ人間だからという理由で同じ写像ということにしておきたい。

世界には、アリスの意識が随伴している物理量とボブの意識が随伴している物理量が存在しているので、世界の状態は、$${\{\{P_i\},\{P_j\}\}}$$と書くことができるだろう。純粋に物理的に捉えれば、アリスの意識を随伴している物理量$${\{P_i\}}$$とボブの意識を随伴している物理量$${\{P_j\}}$$を区別する理由はないので（単に物理量がある（脳の）位置が異なるだけなので）、世界の状態を、

$$
\{P_\lambda | \lambda = i \, or \, j\} = \{\{P_i\},\{P_j\}\}
$$

と書くことにしたい。もう少し数学的に書くならば、アリスの意識を随伴している物理量の添字集合を$${\Lambda_a}$$、ボブの意識を随伴している物理量の添字集合を$${\Lambda_b}$$として、

$$
\{P_{\lambda} \}_{\lambda \in \Lambda_a \cup  \Lambda_b } = \{\{P_i\}_{ i \in \Lambda_a } , \{P_j\}_ { j \in \Lambda_b } \}
$$

と表せられるだろう。メンタルな状態への写像は、$${\{P_\lambda\}_{\lambda \in \Lambda_a \cup  \Lambda_b } }$$を用いて書くならば、

$$
f_{S_2}(\{P_\lambda \}_{\lambda \in \Lambda_a \cup  \Lambda_b } ) = \{ M_a,M_b \}
$$

と書けるだろう。随伴現象説は、上記の$${f_{S_2}(•)}$$という関数が非物理的に存在するということを意味している。

多人数の場合・物も含む場合

世界には、アリスとボブ以外にも多数の人がいる。また、メンタルな状態を随伴していない物理量も存在する（そちらの方がはるかに多い。）。そのため、世界全体を表そうとすると、世界中の全ての独立な物理量を表すための添字集合を$${\Omega}$$として、関数$${f_S(•)}$$に加えて、物理量の集合から物理量の集合の集合への写像$${\Pi}$$が非物理的に存在して、

$$
\Pi: \{P_\lambda \}_{\lambda \in \Omega}  \mapsto \{ \{P_i\}_ { i \in \Lambda_1 }, \{P_j\}_{ j \in \Lambda_2}, \cdots, \{P_k\}_{ k \in \Lambda_N}\}  ,\\  \\
S: \{P_\lambda\}_{ \lambda \in \Lambda_n} \mapsto M_n
$$

と書くのが良いだろう。ここで、$${n \in \mathbb{N}}$$はメンタルな状態を持つ者（人間）を区別する添字であり、$${N \in \mathbb{N}}$$はメンタルな状態を持つ者の数（イメージ的には世界人口）である。随伴現象説とは、上式が成り立つ写像$${\Pi}$$と$${S}$$が非物理的に存在すること（存在するとする説）と同義である。

写像$${\Pi}$$の定義域は、必ずしも世界中の全ての独立な物理量である必要はなく、任意の物理量の組みで良いだろう。すなわち、任意の物理量の添字集合$${\omega}$$に対して、

$$
\Pi: \{P_\lambda \}_{\lambda \in \omega}  \mapsto \{ \{P_i\}_ { i \in \Lambda_1 }, \{P_j\}_{ j \in \Lambda_2}, \cdots, \{P_k\}_{ k \in \Lambda_{\eta(\omega)}}\}
$$

である。ここで、$${\eta(\omega)}$$は、物理量の組み$${\{P_\lambda \}_{\lambda \in \omega}}$$に随伴しているメンタルな状態の数である。

$${\{P_\lambda \}_{\lambda \in \omega}}$$が意識を随伴していない場合（例えば石の物理量のみを含む場合）には、

$$
\Pi: \{P_\lambda \}_{\lambda \in \omega}  \mapsto \{ \} = \varnothing
$$

となる。

あらためて一人の場合の意識随伴の意味

あらためて、どういう場合に意識が物理量に随伴するのかを考えてみたい。それは、ある種の運動方程式（物理量の時間変化を決める式）を$${\{P_\lambda\}_ { \lambda \in \Lambda }}$$が満たしているときであろう。ほとんどの物理量には意識が随伴しないので、極めて特殊な運動方程式に従う物理量のみが意識を随伴すると考えられる。すなわち、$${\{ P_ \epsilon\}_ { \epsilon \in E}}$$を$${\{ P_\lambda\}_ { \lambda \in \Lambda }}$$と直接相互作用する物理量として、関数族のある集合$${\mathfrak{F}_c}$$があり、$${\{f_\lambda\}_ { \lambda \in \Lambda } \in \mathfrak{F}_c}$$を用いて、$${ P_\lambda}$$の運動方程式（物理量の時間微分を決める式）が

$$
\forall \lambda \in \Lambda \quad  \frac{d^{m(\lambda)} P_\lambda}{dt^{m(\lambda)}}  = f_\lambda(\{\frac{d^n P_\xi}{dt^n}\}_{\xi \in \Lambda \cup E, \mathbb{N} \ni n \lt m(\xi)}, \{ P_\xi\}_ { \xi \in \Lambda \cup E})
$$

と書ける場合だろう。ここで、$${m(\lambda)}$$は、物理量$${ P_\lambda}$$の運動方程式の階数である。運動方程式は1階又は2階の微分方程式の場合が多いが、意識を随伴する物理量がどのようなものか不明なため、ここでは任意の階数とした。当然であるが、添字の記号を変更しているだけなので、$${\{P_\lambda\}_ { \lambda \in \Lambda } = \{P_\xi\}_ { \xi \in \Lambda }}$$である。

簡単に表記するために、左辺を右辺に移行した式を、$${\{P_\xi\}_ { \xi \in \Lambda }}$$から導く写像族（作用素族）を$${\{\mathcal{M}_\lambda\}_ { \lambda \in \Lambda } }$$、すなわち、

$$
\mathcal{M}_\lambda {\{ P_\xi\}_ { \xi \in \Lambda }} = -\frac{d^{m(\lambda)} P_\lambda}{dt^{m(\lambda)}} + f_\lambda(\{\frac{d^n P_\xi}{dt^n}\}_{\xi \in \Lambda \cup E(\Lambda), \mathbb{N} \ni n \lt m(\xi)}, \{ P_\xi\}_ { \xi \in \Lambda \cup E(\Lambda)})
$$

と書くことにしたい。作用素の慣例により、カッコの記載は省略している。一般的に作用素は線形とされることが多いが、$${\mathcal{M}_\lambda }$$は線形とは限らない。左辺に$${\{ P_ \epsilon\}_ { \epsilon \in E}}$$が含まれないが、どの物理量と相互作用するかは、自然法則により定まるものであり、すなわち、自然法則により写像$${\Lambda \mapsto E}$$が決まっているので、左辺に$${\{ P_ \epsilon\}_ { \epsilon \in E}}$$がなくとも右辺の$${\{ P_ \epsilon\}_ { \epsilon \in E}}$$は定まる。そのため右辺では$${E(\Lambda)}$$と記載している。

このように定義し、さらに$${\mathfrak{M}_c}$$を意識を随伴する物理量が満たすべき運動方程式を導く作用素族の集合と定義すると、$${\{P_\xi\}_ { \xi \in \Lambda }}$$が意識を随伴しているための条件は、

$$
\exists \{\mathcal{M}_\lambda\}_ { \lambda \in \Lambda } \in \mathfrak{M}_c \quad \forall \lambda \in \Lambda \quad \mathcal{M}_\lambda {\{ P_\xi\}_ { \xi \in \Lambda }} = 0
$$

となる。全ての意識を随伴している物理量の族の集合を$${\mathfrak{P}_c}$$とすると、

$$
\exists \{\mathcal{M}_\lambda\}_ { \lambda \in \Lambda } \in \mathfrak{M}_c \quad \forall \lambda \in \Lambda \quad \mathcal{M}_\lambda {\{ P_\xi\}_ { \xi \in \Lambda }} = 0 \iff \{ P_\xi\}_ { \xi \in \Lambda } \in \mathfrak{P}_c
$$

となる。この命題が、随伴現象説の意味するところ（本質）であると私は考える。そのため、この命題を随伴現象説の基本命題と呼ぶことにしたい。

量子力学の場合

重ね合わせのない場合

量子力学の場合を考えよう。物理量の組みが2つ（$${\{ O_\lambda\}_ { \lambda \in \Lambda }}$$及び$${\{ O_ \epsilon\}_ { \epsilon \in E}}$$）あり、それらのすべての物理量の同時固有状態があり（正確には密度行列とする必要があると見込まれるが本稿の趣旨内では状態と簡易化してもよいだろう）、初期状態が同時固有状態であれば時間進展してもそれらの同時固有状態のままである物理量だと仮定しよう。すなわち、

$$
\forall \mathbb{R} \ni t \ge 0\quad \forall \xi \in \Lambda \cup E \quad O_\xi |\{P_\lambda(t)\}_ {\lambda \in \Lambda}\rangle \otimes |\{P_\epsilon(t)\}_ {\epsilon \in E}\rangle \\
= P_\xi(t)|\{P_\lambda(t)\}_ {\lambda \in \Lambda}\rangle \otimes |\{P_\epsilon(t)\}_ {\epsilon \in E}\rangle ,\\   \\
e^{-\frac{i}{\hbar}Ht}|\{P_\lambda(0)\}_ {\lambda \in \Lambda}\rangle \otimes |\{P_\epsilon(0)\}_{\epsilon \in E}\rangle \\
= e^{i \theta(t)} |\{P_\lambda(t)\}_ {\lambda \in \Lambda}\rangle \otimes |\{P_\epsilon(t)\}_{\epsilon \in E}\rangle
$$

とする。ここで、$${H}$$は、状態の時間発展を決めるハミルトニアン（シュレディンガー表示としている）、$${t}$$は時間パラメータである。$${\theta(t)}$$は任意の実数値関数である。
$${P_\xi(t)}$$は時刻$${t}$$おける物理量$${O_\xi}$$の値である。同じ趣旨であるが、$${O_\xi}$$はq数で、$${P_\xi(t)}$$はc数である。本稿では今後も基本的に$${O}$$の文字はオペレーター（q数）に用いることにする。

さらに、$${\{ P_\lambda\}_ { \lambda \in \Lambda }}$$は、随伴現象説の基本命題の条件を満たすとする。すなわち、

$$
\exists \{\mathcal{M}_\lambda\}_ { \lambda \in \Lambda } \in \mathfrak{M} \quad \forall \lambda \in \Lambda \quad \mathcal{M}_\lambda {\{ P_\xi\}_ { \xi \in \Lambda }} = 0
$$

が成り立つとする。そうすれば、$${\{ P_\lambda\}_ { \lambda \in \Lambda }}$$には意識が随伴している。そうであれば、$${|\{P_\lambda(t)\}_ {\lambda \in \Lambda}\rangle}$$に意識が随伴しているといってもよいだろう。このようにして、随伴現象説は量子論に拡張できる。非量子論の場合と同様に、$${\{ O_\lambda\}_ { \lambda \in \Lambda }}$$は直接的にはそれらの中に含まれる物理量と$${\{ O_ \epsilon\}_ { \epsilon \in E}}$$のみと相互作用すると仮定する（逆にいうと$${\{ O_\lambda\}_ { \lambda \in \Lambda }}$$と相互作用するすべての物理量が$${\{ O_ \epsilon\}_ { \epsilon \in E}}$$に含まれるように集合$${E}$$を定義する。）。

非量子論と同様にメンタルな状態への写像$${S}$$を定義しよう。私（アリス）だけを考慮して、状態が、私の意識が随伴している物理量の固有状態の場合には（時間が経過しても固有状態を継続する場合には）、非量子論の場合と同様に

$$
S: |\{P_i\}_{ i \in \Lambda_a } \rangle \mapsto M_a
$$

とする。ここで、$${\Lambda_a}$$は、私（アリス）の意識を随伴している物理量の添字集合であり、$${|\{P_i\}_{ i \in \Lambda_a } \rangle }$$は、私の意識が随伴している物理量$${\{ O_\lambda\}_ { \lambda \in \Lambda }}$$の値が$${\{P_i\}_{ i \in \Lambda_a } }$$である固有状態である。

アリスとボブがいる場合には、

$$
S_2: |\{P_i\}_{ i \in \Lambda_a } \rangle \otimes |\{P_j\}_{ j \in \Lambda_b } \rangle \mapsto \{M_a,M_b\}
$$

となる。

$$
S_2: |\{P_{\lambda} \}_{\lambda \in \Lambda_a \cup  \Lambda_b } \rangle \mapsto \{M_a,M_b\}
$$

と書いても同じである。

重ねわせのある場合

量子論では、重ね合わせ状態がありえるので、その場合にどう表記するかを検討する必要があるだろう。まず、アリスの意識が随伴している物理量の組みの値が、$${\{P_i\}_{ i \in \Lambda_a } }$$と$${\{Q_i\}_{ i \in \Lambda_a } }$$の状態の重ね合わせ状態、すなわち、$${|\alpha|^2 + |\beta|^2 = 1 }$$として、

$$
\alpha |\{P_i\}_{ i \in \Lambda_a } \rangle + \beta |\{Q_i\}_{ i \in \Lambda_a } \rangle
$$

の状態を考えよう。$${\{P_i\}_{ i \in \Lambda_a }}$$も$${\{Q_i\}_{ i \in \Lambda_a }}$$も随伴現象説の基本命題を満たすとする（以後、基本命題を満たすことは前提として個別には記載しない。）。
物理量の値が異なるからといって、メンタルな状態が異なるとは限らないので、非量子論的な場合に、$${f_S(\{P_i\} ) = f_S(\{Q_i\} ) = M_a}$$の場合をまず考えよう。この場合は、

$$
S:  \alpha |\{P_i\}_{ i \in \Lambda_a } \rangle + \beta |\{Q_i\}_{ i \in \Lambda_a } \rangle \mapsto M_a
$$

とするのが妥当だろう。一方で、$${f_S(\{P_i\} ) \ne f_S(\{Q_i\} ) }$$の場合には、

$$
S:  \alpha |\{P_i\}_{ i \in \Lambda_a } \rangle + \beta |\{Q_i\}_{ i \in \Lambda_a } \rangle \mapsto \varnothing
$$

とするのが良いだろう。意識の特徴は、常に1つに統合されていることであり、$${\alpha |\{P_i\}\rangle + \beta |\{Q_i\} \rangle}$$はそうした状態ではないからである（ただし、$${\alpha |\{P_i\} _{ i \in \Lambda_a } \rangle + \beta |\{Q_i\} _{ i \in \Lambda_a }  \rangle = |\{R_i\} _{ i \in \Xi }  \rangle }$$で随伴現象説の基本命題を満たす物理量の組み$${\Xi}$$がある場合（もう少し詳しく書くと物理量族$${\{O_\xi\}_{\xi \in \Xi}}$$があり$${ |\{R_i\} _{ i \in \Xi }  \rangle }$$がその固有状態の場合）は除く（こうした物理量の組みは存在するとは考え難いので今後は考慮しない。）。）。$${\varnothing}$$は特定のメンタルな状態が随伴していないことを意味する。

異時刻間の人格・意識の同一性について

$${\alpha |\{P_i(t)\}_{ i \in \Lambda_a}\rangle + \beta |\{Q_i (t)\}_{ i \in \Lambda_a}\rangle}$$には意識は随伴しないが、$${ |\{P_i(t)\}_{ i \in \Lambda_a }  \rangle }$$と$${ |\{Q_i(t)\}_{ i \in \Lambda_a } \rangle}$$にはそれぞれ意識、$${f_S(\{P_i(t)\}_{ i \in \Lambda_a }  ) }$$及び$${f_S(\{Q_i(t)\}_{ i \in \Lambda_a }  ) }$$が随伴している。この2つの意識は別の（異なる）意識であるが、どちらの意識も自分はアリスだと認識しているだろう。これは、どのようにして起こるのだろうか（あり得ないことではないだろうか。)。ところが、これはそれほど不思議でもなく、単純に、ある時刻$${t_0}$$があり、$${t \le t_0}$$において、$${\forall i \in \Lambda_a \quad P_i(t)=Q_i(t)}$$ということであろう。$${t \gt t_0}$$において異なる意識を随伴している状態であるが、意識は過去からの同一性を感じるものであるので、いずれも過去の同じだった時から自らのみが唯一続いていると感じている。そのように感じる運動方程式（過去との同一性の認識を持つ意識を随伴する物理値の組の運動方程式）$${\forall \lambda \in \Lambda \quad \mathcal{M}_\lambda {\{ P_\xi\}_ { \xi \in \Lambda_a }} = 0 }$$を満たしている。意識を決めているのは、$${\{P_i\}_{ i \in \Lambda_a }}$$であるから、それが同じであれば、非量子論の場合に異時刻間の自己同一性を感じるのであれば（異時点間で自己同一性を感じることも随伴現象説に含まれると本稿では考える。）、量子論の場合にも感じることになる。

それでは、こうした異なる（2つの）意識が同じアリスだと思っている状態の重ね合わせの状態は、どういう場合に発生するのだろうか。それは、例えば（例えばなので他にもあるが）、$${t \le t_0}$$において、状態が、

$$
|\{P_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{P_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes ( \alpha e^{\theta_1(t)} | \{P_x (t)\}_{ x \in X} \rangle + \beta e^{\theta_2(t)} | \{Q_x (t)\}_{ x \in X}  \rangle )
$$

にあるような場合であろう。正確な表現ではないが、$${t \le t_0}$$においては$${ \alpha e^{\theta_1(t)} | \{P_x(t)\}_{ x \in X} \rangle + \beta e^{\theta_2(t)} | \{Q_x(t)\}_{ x \in X} \rangle}$$はアリスから離れた位置にある系の状態であり、アリスに影響を与えることはない（アリスと相互作用しない）が、時間の経過とともに相互作用するように（影響を与えるように）なり、そうすると、状態は、

$$
\alpha e^{\theta_1(t)} |\{P_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{P_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes  | \{P_x (t)\}_{ x \in X} \rangle \\
+ \beta e^{\theta_2(t)} |\{Q_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{Q_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes  | \{Q_x (t)\}_{ x \in X} \rangle
$$

となる。このようにして、同じアリスであるという認識を持つ異なる意識の重ね合わせの状態ができる。ただし、ここでは、式をシンプルにするために、物理量$${\{O_x\}_{x \in X}}$$は、非量子論的な物理量であるとした。すなわち、その固有状態が時間が経過しても固有状態のままの物理量である（加えて、$${\{O_x\}_{x \in X}}$$と$${\{O_\epsilon\}_{\epsilon \in E_a}}$$の相互作用も非量子論的で状態は固有状態のままであるとしている。）。これは、例えばシュレディンガーの猫を私（アリス）が見たケースの式である。$${ \alpha e^{\theta_1(t)} | \{P_x(t)\}_{ x \in X} \rangle + \beta e^{\theta_2(t)} | \{Q_x(t)\}_{ x \in X} \rangle}$$が生きた猫と死んだ猫の重ね合わせ状態であり、$${|\{P_i(t)\}_{ i \in \Lambda_a} \rangle}$$は生きた猫を見たと思っている私の意識が随伴している状態である。$${|\{Q_i(t)\}_{ i \in \Lambda_a} \rangle}$$の方が死んだ猫を見たと思っている私の意識が随伴している状態である。

異時点間の人格の同一性（ここでいう同一性は客観的なものではなく単に自らが過去の自分の未来であると思うか否かということである。）は、量子論の運動方程式$${|t\rangle = e^{-\frac{i}{\hbar}Ht} |t=0\rangle}$$を用いて時間を逆向きに進めたとき（過去の時刻の状態を計算したとき）に実現する状態かどうかであると考えると良いだろう。$${|\{Q_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{Q_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes  | \{Q_x (t)\}_{ x \in X} \rangle }$$から量子論の運動方程式を用いて過去の時間の状態を計算すると、

$$
e^{-\frac{i}{\hbar}H(t_0-t)} e^{\theta_2(t)} |\{Q_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{Q_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes  | \{Q_x (t)\}_{ x \in X} \rangle \\
= e^{\theta_2(t)} |\{P_i(t_0)\}_{ i \in \Lambda_a} \rangle \otimes |\{P_\epsilon (t_0)\}_{ \epsilon \in E_a} \rangle \otimes | \{Q_x (t_0)\}_{ x \in X}  \rangle
$$

となる。従って、$${|\{Q_i(t)\}_{ i \in \Lambda_a} \rangle }$$に随伴する意識と$${|\{P_i(t_0)\}_{ i \in \Lambda_a} \rangle }$$に随伴する意識は継続性のある意識である。異なる状態（$${|\{P_i(t)\}_{ i \in \Lambda_a} \rangle }$$と$${|\{Q_i(t)\}_{ i \in \Lambda_a} \rangle }$$）に随伴している異なる意識が過去の同じ状態（$${|\{P_i(t_0)\}_{ i \in \Lambda_a} \rangle }$$）に随伴している意識を過去の自分だと考えていても特に問題は（矛盾は）ないだろう。

二人が重ね合わせの状態になる場合

次に、アリスとボブの2人と、シュレディンガーの猫がいる状態を考えよう。すなわち、時刻$${t \le t_0}$$において、状態が、

$$
|\{P_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{P_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \\
\otimes ( \alpha | \{P_x (t)\}_{ x \in X} \rangle + \beta | \{Q_x (t)\}_{ x \in X}  \rangle ) \\
\otimes |\{P_i(t)\}_{ i \in \Lambda_b} \rangle \otimes |\{P_\epsilon (t)\}_{ \epsilon \in E_b} \rangle
$$

である場合を考える（以後、前節まで記載していた状態の位相（前節の $${e^{\theta_1(t)},e^{\theta_2(t)}}$$の記載を省略する。量子論では、干渉が発生する原因であり非常に重要な要素であるが、非量子論的な物理量の値に随伴している意識について考察する本稿では重要な役割を果たさず、記載しなくても論旨に影響がないためである。）。

時刻$${t_1 \gt t_0}$$において、アリスが猫を見て、ボブはまだ見ていない場合（$${|\{P_\epsilon (t)\}_{ \epsilon \in E_a} \rangle}$$と$${\alpha | \{P_x (t)\}_{ x \in X} \rangle + \beta | \{Q_x (t)\}_{ x \in X}  \rangle}$$が相互作用しているが、$${|\{P_\epsilon (t)\}_{ \epsilon \in E_b} \rangle}$$と$${\alpha | \{P_x (t)\}_{ x \in X} \rangle + \beta | \{Q_x (t)\}_{ x \in X}  \rangle}$$は空間的に離れていてまだ相互作用していない場合）、状態は、時刻$${t \gt  t_1}$$において、

$$
(\alpha |\{P_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{P_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes  | \{P_x (t)\}_{ x \in X} \rangle \\
+ \beta |\{Q_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{Q_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes  | \{Q_x (t)\}_{ x \in X} \rangle ) \\
\otimes |\{P_i(t)\}_{ i \in \Lambda_b} \rangle \otimes |\{P_\epsilon (t)\}_{ \epsilon \in E_b} \rangle
$$

になる。その後、時刻$${t_2 \gt  t_1}$$において、ボブがシュレディンガーの猫を見たとすると、状態は、

$$
\alpha |\{P_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{P_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes  | \{P_x (t)\}_{ x \in X} \rangle \otimes |\{P_i(t)\}_{ i \in \Lambda_b} \rangle \otimes |\{P_\epsilon (t)\}_{ \epsilon \in E_b} \rangle \\
+ \beta |\{Q_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{Q_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes  | \{Q_x (t)\}_{ x \in X} \rangle \otimes |\{Q_i(t)\}_{ i \in \Lambda_b} \rangle \otimes |\{Q_\epsilon (t)\}_{ \epsilon \in E_b} \rangle
$$

になる。ボブがその後にアリスにあって話をしても、状態は2つの状態の重ね合わせの状態であることには変わりはない。それは、簡単のために、相互作用が非量子論的であり固有状態は固有状態のまま物理値が決定論的な運動方程式に従い変化するのみと仮定しているからである。言い換えると、全ての物理量$${\{O_\xi\}_{\xi \in \Lambda_a \cup \Lambda_b \cup E_a \cup E_b \cup X}}$$及びその間の相互作用は非量子論的と仮定している。

上記では、ボブが猫を見たのちにアリスと話をする場合を考えたが、逆にアリスとボブが話をした後にボブが始めて猫を見たとしても、状態は、

$$
\alpha |\{P^\prime_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{P ^\prime_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes  | \{P ^\prime_x (t)\}_{ x \in X} \rangle \otimes |\{P ^\prime_i(t)\}_{ i \in \Lambda_b} \rangle \otimes |\{P ^\prime_\epsilon (t)\}_{ \epsilon \in E_b} \rangle \\
+ \beta |\{Q ^\prime_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{Q ^\prime_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes  | \{Q ^\prime_x (t)\}_{ x \in X} \rangle \otimes |\{Q ^\prime_i(t)\}_{ i \in \Lambda_b} \rangle \otimes |\{Q ^\prime_\epsilon (t)\}_{ \epsilon \in E_b} \rangle
$$

という形になることで変わりはない。ただし物理値は異なっているので、プライムをつけている。なお、時間進展は量子論においても決定論であるため、これは、時刻$${t \le t_0}$$において、状態が、

$$
|\{P_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{P_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \\
\otimes ( \alpha | \{P_x (t)\}_{ x \in X} \rangle + \beta | \{Q_x (t)\}_{ x \in X}  \rangle ) \\
\otimes |\{P ^\prime_i(t)\}_{ i \in \Lambda_b} \rangle \otimes |\{P ^\prime_\epsilon (t)\}_{ \epsilon \in E_b} \rangle
$$

と異なる状態にあったということを一般的には意味する（他の可能性が全くないわけではないが）。アリスと猫については異なる状態である必要はないので、プライムはつけていない（ボブにだけプライムをつけている。）。

異なる意識間の意思疎通のより正確な説明（アリスとボブの相互作用とは）

前節では、物理量$${\{O_\xi\}_{\xi \in \Lambda_a \cup \Lambda_b \cup E_a \cup E_b \cup X}}$$のみを記載し、それらの物理量が直接相互作用するように記載したが、これは本当は正しくない。例えば$${\{O_\epsilon\}_{\epsilon \in E_a}}$$と$${\{O_\epsilon\}_{\epsilon \in E_b}}$$は離れた位置の物理量であるため直接相互作用することはなく、2人の体や2人の間の空間の物理量を通してしか相互作用することはない。例えば話をする場合は口や舌の形状を表す物理量やアリスとボブの間の空気の密度、圧力、流速などの空間分布といった物理量が必要だろう（口や舌の形状も密度や張力の空間分布で表すことができるだろう。）。正確には、これらの、$${\{O_\xi\}_{\xi \in E_a \cup E_b \cup X}}$$が相互作用するための物理量を全て含めて記載する必要がある。こうした必要な物理量の全体を$${\{O_\xi\}_{\xi \in \Omega}}$$とすると、正確には前節では、$${\{O_\xi\}_{\xi \in \Lambda_a \cup \Lambda_b \cup E_a \cup E_b \cup X \cup \Omega}}$$の全ての物理量とその間の相互作用が非量子論的と仮定していたということである（その仮定をおかない検討は後述する。）。

本稿では、前述した物理量（オペレータ）間の直接の相互作用の有無の他に、部分系の重ね合わせの状態のうちの一つの状態が他の部分系の重ね合わせの状態のうち一つの状態と相互作用するか否かということを考える。これは、

$$
(\alpha |\{P_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{P_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes |\{P_i(t)\}_{ i \in \Lambda_b} \rangle \otimes |\{P_\epsilon (t)\}_{ \epsilon \in E_b} \rangle \otimes |\{P_\xi (t)\}_{ \xi \in \Omega_e(t)} \rangle \\
+ \beta |\{Q_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{Q_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes |\{Q_i(t)\}_{ i \in \Lambda_b} \rangle \otimes |\{Q_\epsilon (t)\}_{ \epsilon \in E_b} \rangle \otimes |\{Q_\xi (t)\}_{ \xi \in \Omega_e(t)}) \\
\otimes |\{P_\xi (t)\}_{ \xi \in \Omega \setminus \Omega_e(t)})
$$

という状態にあったときに（$${\Omega}$$は前段の物理的な意味で$${\{O_\xi\}_{\xi \in E_a}}$$と$${\{O_\xi\}_{\xi \in E_b}}$$が相互作用するために必要な物理量の添字集合であり、$${\Omega_e(t)}$$はそのうち時刻$${t}$$において既に相互作用している物理量の添字集合である。従って、$${\{O_\xi \}_{ \xi \in \Omega \setminus \Omega_e(t)}}$$は時刻$${t}$$以降に$${\{O_\xi\}_{\xi \in E_a \cup E_b}}$$と相互作用する可能性がある物理量ということになる。）、$${ f_S(\{P_i\}_{i \in \Lambda_a} )}$$の意識を持つアリスは、$${ f_S(\{Q_i\} _{i \in \Lambda_b} )}$$の意識を持つボブと意思疎通ができるか（アリスの意識が随伴する状態とボブの意識が随伴する状態は相互作用ができるか）という観点である。

これを考えるには、仮想的に時刻$${t}$$において異なる状態（様相論理の可能世界に倣って可能状態と呼ぶことにしたい。）

$$
(\alpha |\{P_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{P_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes |\{P_i(t)\}_{ i \in \Lambda_b} \rangle \otimes |\{P_\epsilon (t)\}_{ \epsilon \in E_b} \rangle \otimes |\{P_\xi (t)\}_{ \xi \in \Omega_e(t)} \rangle \\
+ \beta |\{Q_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{Q_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes |\{Q^{\prime}_i(t)\}_{ i \in \Lambda_b} \rangle \otimes |\{Q^{\prime}_\epsilon (t)\}_{ \epsilon \in E_b} \rangle \otimes |\{Q^{\prime}_\xi (t)\}_{ \xi \in \Omega_e(t)}) \\
\otimes |\{P_\xi (t)\}_{ \xi \in \Omega \setminus \Omega_e(t)})
$$

にあるとしたときに、$${t}$$以降の時刻$${\tau}$$において$${ \{P_i(\tau)\}_{i \in \Lambda_a} }$$の値が変わるかを考えれば良いように思われる。そのために、

$$
e^{-\frac{i}{\hbar}H(\tau - t)}
(\alpha |\{P_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{P_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes |\{P_i(t)\}_{ i \in \Lambda_b} \rangle \otimes |\{P_\epsilon (t)\}_{ \epsilon \in E_b} \rangle \otimes |\{P_\xi (t)\}_{ \xi \in \Omega_e(t)} \rangle \\
+ \beta |\{Q_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{Q_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes |\{Q^{\prime}_i(t)\}_{ i \in \Lambda_b} \rangle \otimes |\{Q^{\prime}_\epsilon (t)\}_{ \epsilon \in E_b} \rangle \otimes |\{Q^{\prime}_\xi (t)\}_{ \xi \in \Omega_e(t)}) \\
\otimes |\{P_\xi (t)\}_{ \xi \in \Omega \setminus \Omega_e(t)}) \\
= (\alpha |\{P ^{\prime}_i(\tau)\}_{ i \in \Lambda_a} \rangle \otimes |\{P ^{\prime}_\epsilon (\tau)\}_{ \epsilon \in E_a} \rangle \otimes |\{P ^{\prime}_i(\tau)\}_{ i \in \Lambda_b} \rangle \otimes |\{P ^{\prime}_\epsilon (\tau)\}_{ \epsilon \in E_b} \rangle \otimes |\{P ^{\prime}_\xi (\tau)\}_{ \xi \in \Omega ^{\prime}_e(\tau)} \rangle \\
+ \beta |\{Q ^{\prime}_i(\tau)\}_{ i \in \Lambda_a} \rangle \otimes |\{Q ^{\prime}_\epsilon (\tau)\}_{ \epsilon \in E_a} \rangle \otimes |\{Q^{\prime}_i(\tau)\}_{ i \in \Lambda_b} \rangle \otimes |\{Q^{\prime}_\epsilon (\tau)\}_{ \epsilon \in E_b} \rangle \otimes |\{Q^{\prime}_\xi (\tau)\}_{ \xi \in \Omega ^{\prime}_e(t)}) \\
\otimes |\{P ^{\prime}_\xi (\tau)\}_{ \xi \in \Omega \setminus \Omega ^{\prime}_e(\tau)})
$$

により$${ \{P^{\prime}_i(\tau)\}_{i \in \Lambda_a} }$$を定義する。そうすると、$${\forall i \in \Lambda_a \, \forall \tau \ge t \quad P^{\prime}_i(\tau) = P_i(\tau)}$$となるだろう。なぜならば、$${e^{-\frac{i}{\hbar}H(\tau - t)}}$$の作用は線形だからである。すなわち、$${\{Q_i(t)\} _{i \in \Lambda_b \cup E_b}}$$の値によって、$${ f_S(\{P_i(\tau)\}_{i \in \Lambda_a} )}$$が変わることはないということである。このことをもって、筆者は、意識$${ f_S(\{P_i(t)\}_{i \in \Lambda_a} )}$$と意識$${ f_S(\{Q_i(t)\}_{i \in \Lambda_b} )}$$は意思疎通することはない、意思疎通できないと表現して良いと考える。意識$${ f_S(\{P_i(t)\}_{i \in \Lambda_a} )}$$は意識$${ f_S(\{Q_i(t)\}_{i \in \Lambda_b} )}$$の存在を認知しない、認知できないと表現しても良いだろう。

$${|\{P_i(t)\}_{ i \in \Lambda_b} \rangle }$$が$${|\{P^{\prime}_i(t)\}_{ i \in \Lambda_b} \rangle }$$に変わる可能状態を考えると、$${ \exists i \in \Lambda_a \quad P^{\prime}_i(\tau) \ne P_i(\tau)}$$となりえるので、意識$${ f_S(\{P_i(t)\}_{i \in \Lambda_a} )}$$は意識$${ f_S(\{P_i(t)\}_{i \in \Lambda_b} )}$$の存在を認知できて、意思疎通できるといえる。

片方が意識を随伴する状態であれば、もう片方は意識を随伴する状態でなくても、同様の方法により、存在を認知できる状態か、すなわちクオリアを生じえる状態かを検討することができる。

両方とも意識を随伴しない状態の場合にも、非量子論的な物理量の同時固有状態の場合には、相互作用しえる状態かどうかを検討することができる。

量子論的な物理量を含むシンプルなケース（スピンの向きの測定）

これまでの考察は、重ね合わせの状態は考えるものの、物理量は全て非量子論的な物理量のみ扱ってきた。本節では、最も単純な量子論的な物理量を考えよう。それは、例えば電子のスピンである。その物理量を$${O_{s_{0,0}}}$$としよう。物理量$${O_{s_{0,0}}}$$は、値として$${\frac{1}{2}}$$と$${-\frac{1}{2}}$$をとる。値$${\frac{1}{2}}$$の固有状態を$${|0,0,+\rangle}$$と、値$${-\frac{1}{2}}$$の固有状態を$${|0,0,-\rangle}$$と書くことにする。スピンは、相互作用することで、非量子論的な物理量の固有状態を異なる値の2つの固有状態の重ね合わせにする相互作用を持つ物理量である。すなわち、$${A}$$をスピンの測定措置を構成する物理量の添字集合とすると、測定装置の向き$${\theta = f_\theta(\{P_i\}_{i \in A} )}$$及び$${\phi = f_\phi(\{P_i\}_{i \in A} )}$$を用いて、初期状態

$$
|\{P_i(t_0)\}_{i \in \Lambda_a} \rangle \otimes |\{ P_i(t_0)\}_{i \in A} \rangle \otimes |0,0,+ \rangle
$$

は時間が経過すると（測定結果を私（アリス）が見たら）、

$$
\alpha(\theta,\phi ) |\{P_i(t)\}_{i \in \Lambda_a} \rangle \otimes |\{ P_i(t)\}_{i \in A} \rangle \otimes |\theta,\phi,+ \rangle \\
+ \beta( \theta,\phi ) |\{Q_i(t)\}_{i \in \Lambda_a} \rangle \otimes |\{ Q_i(t)\}_{i \in A} \rangle
\otimes |\theta,\phi,- \rangle
$$

の状態になると書ける。ただし、式を簡易にするために主要な系以外については記載を省略している。また、従来同様に$${\{O_i\}_{i \in A\cup \Lambda_a}}$$の相互作用は非量子論的と仮定している。なお、当然であるが

$$
\alpha^2( \theta,\phi )＋ \beta^2(\theta,\phi ) = 1
$$

である。

$${ f_S( |\{P_i(t)\}_{i \in \Lambda_a} \rangle)}$$の意識の私（アリス）には、測定装置が$${\frac{1}{2}}$$の測定値を示しているクオリアが生じている。$${ f_S( |\{Q_i(t)\}_{i \in \Lambda_a} \rangle)}$$の意識の私（アリス）には、測定装置が$${-\frac{1}{2}}$$測定値を示しているクオリアが生じている。

次に、私（アリス）と別人（ボブ）がいて、それぞれに測定装置を持っていて、状態$${|0,0,+ \rangle}$$のスピンを測定するケースを考えよう。すなわち、初期状態

$$
|\{P_i(t_0)\}_{i \in \Lambda_a} \rangle \otimes |\{ P_i(t_0)\}_{i \in A_a} \rangle \otimes |0,0,+ \rangle_a \otimes |\{P_i(t_0)\}_{i \in \Lambda_b} \rangle \otimes |\{ P_i(t_0)\}_{i \in A_b} \rangle \otimes |0,0,+ \rangle_b
$$

からの時間進展を考えよう。$${|0,0,+ \rangle_a}$$は私（アリス）が測定するスピンの状態、$${|0,0,+ \rangle_b}$$はボブが測定するスピンの状態である。

私（アリス）とボブがそれぞれに測定結果を確認しお互いに接触していない状況では、

$$
(\alpha(\theta_a,\phi_a ) |\{P_i(t)\}_{i \in \Lambda_a} \rangle \otimes |\{ P_i(t)\}_{i \in A_a} \rangle \otimes |\theta_a,\phi_a,+ \rangle_a \\
+ \beta( \theta_a,\phi_a ) |\{Q_i(t)\}_{i \in \Lambda_a} \rangle \otimes |\{ Q_i(t)\}_{i \in A_a} \rangle
\otimes |\theta_a,\phi_a,- \rangle_a) \\
\otimes (\alpha(\theta_b,\phi_b ) |\{P_i(t)\}_{i \in \Lambda_b} \rangle \otimes |\{ P_i(t)\}_{i \in A_b} \rangle \otimes |\theta_b,\phi_b,+ \rangle_b \\
+ \beta( \theta_b,\phi_b) |\{Q_i(t)\}_{i \in \Lambda_b} \rangle \otimes |\{ Q_i(t)\}_{i \in A_b} \rangle
\otimes |\theta_b,\phi_b,- \rangle_b)
$$

の状態になる。ここで、$${\theta_x,\phi_x  \quad x \in \{a,b\}}$$は、それぞれアリスとボブの測定装置の角度、すなわち、$${\vartheta_x= f_{\vartheta}(\{P_i\}_{i \in A_x} ) \quad \vartheta \in \{\theta,\phi\} \quad x \in \{a,b\} }$$である。

さらに時間が進み、私（アリス）とボブがあったとすると

$$
\alpha_a \alpha_b |\{P_i(t)\}_{i \in \Lambda_a} \rangle \otimes  |\{P_i(t)\}_{i \in \Lambda_b} \rangle \otimes |\{ P_i(t)\}_{i \in A_a} \rangle  \otimes |\{ P_i(t)\}_{i \in A_b} \rangle \otimes |\theta_a,\phi_a,+ \rangle_a \otimes |\theta_b,\phi_b,+ \rangle_b \\
+ \beta_a  \alpha_b |\{V_i(t)\}_{i \in \Lambda_a} \rangle \otimes  |\{V_i(t)\}_{i \in \Lambda_b} \rangle \otimes |\{ V_i(t)\}_{i \in A_a} \rangle \otimes |\{ V_i(t)\}_{i \in A_b} \rangle
\otimes |\theta_a,\phi_a,- \rangle_a \otimes |\theta_b,\phi_b,+ \rangle_b \\
+ \alpha_a \beta_b |\{W_i(t)\}_{i \in \Lambda_a} \rangle \otimes  |\{W_i(t)\}_{i \in \Lambda_b} \rangle \otimes |\{ W_i(t)\}_{i \in A_a} \rangle  \otimes |\{ W_i(t)\}_{i \in A_b} \rangle \otimes |\theta_a,\phi_a,+ \rangle_a \otimes |\theta_b,\phi_b,- \rangle_b \\
+ \beta_a  \beta_b |\{Q_i(t)\}_{i \in \Lambda_a} \rangle \otimes  |\{Qi(t)\}_{i \in \Lambda_b} \rangle \otimes |\{ Q_i(t)\}_{i \in A_a} \rangle \otimes |\{ Q_i(t)\}_{i \in A_b} \rangle
\otimes |\theta_a,\phi_a,- \rangle_a \otimes |\theta_b,\phi_b,- \rangle_b
$$

の状態になる。ただし、

$$
\alpha_x = \alpha (\theta_x,\phi_x ) \quad x \in \{a,b\}, \\
\beta_x = \beta (\theta_x,\phi_x ) \quad x \in \{a,b\}
$$

として式を簡略化した。$${f_S(|\{P_i(t)\}_{i \in \Lambda_a} \rangle) }$$は、自分（アリス）もボブも共に$${\frac{1}{2}}$$のスピンを測定したという意識であり、その意識はこの後（時刻的に後で）、前節の実際と少し異なる仮想状態が物理量の値（自らの意識が随伴している状態を特定する物理量の値）に違いをもたらすことはないという意味で、例えば$${f_S(|\{V_i(t)\}_{i \in \Lambda_b} \rangle) }$$と意思疎通することはない。すなわち、意識$${f_S(|\{P_i(t)\}_{i \in \Lambda_a} \rangle) }$$にとって実在するのは$${f_S(|\{P_i(t)\}_{i \in \Lambda_b} \rangle) }$$を随伴しているボブだけであり、$${f_S(|\{V_i(t)\}_{i \in \Lambda_b} \rangle) }$$、$${f_S(|\{W_i(t)\}_{i \in \Lambda_b} \rangle) }$$、$${f_S(|\{Q_i(t)\}_{i \in \Lambda_b} \rangle) }$$の意識を随伴するボブはいないのと同じである。同様に、ボブの意識の一つである$${f_S(|\{V_i(t)\}_{i \in \Lambda_b} \rangle) }$$にとって実在するアリスは、$${f_S(|\{V_i(t)\}_{i \in \Lambda_a} \rangle) }$$を随伴しているアリスだけであり、$${f_S(|\{P_i(t)\}_{i \in \Lambda_a} \rangle) }$$、$${f_S(|\{W_i(t)\}_{i \in \Lambda_a} \rangle) }$$、$${f_S(|\{Q_i(t)\}_{i \in \Lambda_a} \rangle) }$$の意識を随伴するアリスはいないのと同じである。

波束の収束（射影仮説）と随伴現象説

意識$${f_S(|\{P_i(t)\}_{i \in \Lambda_a} \rangle) }$$にとって実在するのは$${f_S(|\{P_i(t)\}_{i \in \Lambda_b} \rangle) }$$を随伴しているボブだけであり、$${f_S(|\{V_i(t)\}_{i \in \Lambda_b} \rangle) }$$、$${f_S(|\{W_i(t)\}_{i \in \Lambda_b} \rangle) }$$、$${f_S(|\{Q_i(t)\}_{i \in \Lambda_b} \rangle) }$$の意識を随伴するボブは存在しないように、意識$${f_S(|\{P_i(t)\}_{i \in \Lambda_a} \rangle) }$$にとって、測定装置$${|\{ V_i(t)\}_{i \in A_a} \rangle }$$、$${ |\{ V_i(t)\}_{i \in A_b} \rangle }$$、スピンの状態$${ |\theta_a,\phi_a,- \rangle_a}$$、$${ |\theta_b,\phi_b,- \rangle_b }$$は存在しないのと同じである。一方、意識$${f_S(|\{P_i(t)\}_{i \in \Lambda_a} \rangle) }$$にとって、測定装置$${|\{ P_i(t)\}_{i \in A_a} \rangle }$$、$${ |\{ P_i(t)\}_{i \in A_b} \rangle }$$、スピンの状態$${ |\theta_a,\phi_a,+ \rangle_a}$$は存在している（その存在の意味するところは、前々節で記載したように、現実と異なる仮想状態を考えた際に私の意識が異なりえるということである。）。もともと時刻$${t_0}$$では、$${|0,0,+ \rangle_a}$$であった状況が、$${ |\theta_a,\phi_a,- \rangle_a}$$がなく、$${ |\theta_a,\phi_a,+ \rangle_a}$$がある状況になったということは、量子力学でいう波束の収束（射影仮説が起こるとしていること）が意識$${f_S(|\{P_i(t)\}_{i \in \Lambda_a} \rangle) }$$にとって起こっているということである。同様に、意識$${f_S(|\{V_i(t)\}_{i \in \Lambda_a} \rangle) }$$、意識$${f_S(|\{W_i(t)\}_{i \in \Lambda_a} \rangle) }$$、意識$${f_S(|\{W_i(t)\}_{i \in \Lambda_a} \rangle) }$$にも波束の収束が起こっている。このように一部の物理量$${O_{s_{0,0}}}$$を除いてその他の物理量が非量子論的な物理量であり、意識が特定の運動方程式を満たす物理値に随伴するのであれば、ユニタリな時間進展に加えて射影仮説のような公理を追加しなくても、意識が認識する実験結果には射影が起こる。つまり、量子力学の実験結果を説明するために、射影仮説は不要ということである。随伴現象説を適切に量子論に拡張できれば、射影仮説は不要になる可能性があるといえるだろう。

非可算無限個のアリスの重ね合わせ状態

最後に、一般的な量子論の場合を考察しよう。量子論では一般的に状態は、波動関数$${\psi \in \mathbb{C}}$$で表される重ね合わせ状態である。すなわち、

$$
|\{P_i(t)\}_{ i \in \Lambda_a} \rangle \otimes |\{P_\epsilon (t)\}_{ \epsilon \in E_a} \rangle \otimes \prod_{i \in \Omega} \int \! dq_i \, \psi(t,\{q_i\}_{ i \in \Omega})| \{q_i\}_{ i \in \Omega} \rangle
$$

のような状態から時間発展していくことが普通だろうと考えられる。複数の変数がある状態を記載するのは複雑であるため（論旨以外のところで複雑になり理解を妨げるため）、シンプルに1変数の状態で簡略化して記載することにしよう（上記の式でも、$${\Omega}$$が離散的な集合であることを前提としており、連続的な場合を表せていない簡略した式になっているが、それでも理解を妨げると思われる。）。すなわち、

$$
|P_i(t_0) \rangle \otimes |P_\epsilon (t_0) \rangle \otimes \int \! dq \, \psi(t_0,q)| q \rangle
$$

の状態からの時間発展を考える（それぞれの部分系に対応した物理量として、$${O_i,O_\epsilon,O_q}$$を考える。）。これは、時間が経過すれば、時刻$${t \gt t_0}$$として、

$$
\int \! dq \,\,\int \!dQ_\epsilon \,\, \int \! dQ_i \,\,\Psi_{[P_i(t_0),P_\epsilon(t_0),\psi(t_0,\cdot)]} (t,Q_i,Q_\epsilon,q)|Q_i\rangle \otimes |Q_\epsilon \rangle \otimes | q \rangle
$$

の状態となるだろう。ここで、$${\Psi}$$の引数を$${[P_i(t_0),P_\epsilon(t_0),\psi(t_0,\cdot)]}$$と$${(t,Q_i,Q_\epsilon,q)}$$に分けたのは、$${|Q_i\rangle \otimes |Q_\epsilon \rangle \otimes | q \rangle}$$の重ね合わせの係数という観点の$${\Psi(Q_i,Q_\epsilon,q)}$$とその形状を決めている引数$${[P_i(t_0),P_\epsilon(t_0),\psi(t_0,\cdot)]}$$という観点の違いがあることを示す趣旨からである。ちなみに、$${\psi(t_0,\cdot)}$$は、$${\{\psi(t_0, q)\}_{q \in \mathbb{R}}}$$の意味（省略記法）である。

私（アリス）の意識を随伴している状態のみを取り出すと、物理量$${O_q}$$の部分系を無視して、状態は、

$$
\int \! dQ_i \,\,\Psi_{[P_i(t_0),P_\epsilon(t_0),\psi(t_0,\cdot)]} (t,Q_i)|Q_i\rangle
$$

となる。通常の量子力学のように、$${Q_i \in \mathbb{R}}$$だとすると、私（アリス）は非加算無限の濃度での連続的な重ね合わせの状態になるということである。

ここから$${O_i}$$の値が$${P_i}$$である固有状態を抜き出す（通常の量子力学の用語では射影する）と、もとの状態は、

$$
|P_i\rangle \otimes \int \! dQ_\epsilon \,\,\Psi (t,Q_\epsilon) |Q_\epsilon \rangle
$$

になる。$${O_i}$$が意識を随伴する物理量であることから、$${O_i}$$が非量子論的であり、かつ$${O_i}$$と$${O_\epsilon}$$の相互作用が非量子論的であったとしても、上記は$${O_\epsilon}$$の異なる固有値の状態の重ね合わせの状態になりえる。それは、経路$${\{P_\epsilon(\tau)\}_{t_0 \le \tau \le 2t}}$$における運動方程式の解を$${\{P_i(\tau)\}_{t_0 \le \tau \le 2t}}$$、経路$${\{Q_\epsilon(\tau)\}_{t_0 \le \tau \le 2t}}$$おける解を$${\{Q_i(\tau)\}_{t_0 \le \tau \le 2t}}$$とした場合に、$${P_i(t) = Q_i(t)}$$、$${P_\epsilon(t) \ne Q_\epsilon(t)}$$の場合がありえるからである。

一方で、$${\tau \gt t}$$においては、再び$${P_i(\tau) \ne Q_i(\tau)}$$となるだろう（決定論的な運動方程式で異なる値の物理値と相互作用すれば異なる値になると考えられるからである（これに対して相互作用が量子論的で相互作用の結果重なりあわせの状態になる場合、異なる値の物理量との相互作用の結果同じ値の固有状態が重なり合わせの中に含まれる可能性があるため、前述の推論は成り立たない。）。）。したがって、意識を随伴する物理量の値の経路$${\{P_i(\tau)\}_{t_0 \le \tau \le 2t}}$$の時刻$${t}$$における状態は、物理量$${O_\epsilon}$$についても物理量の値が決まっている固有状態

$$
|P_i(t)\rangle \otimes |P_\epsilon (t)\rangle
$$

であると考えると良いと思われる（随伴現象説を量子論に拡張できそうに思われる。）。

すなわち、$${O_i}$$と$${O_\epsilon}$$の相互作用が非量子論的であれば、$${O_\epsilon}$$と$${O_q}$$の相互作用が量子論的であっても、$${O_i}$$と$${O_\epsilon}$$の両方の物理量の同時固有状態の時間発展の経路$${\{P_i(\tau)\}_{t_0 \le \tau}}$$及び$${\{P_\epsilon(\tau)\}_{t_0 \le \tau}}$$を考えることができるということである。

量子論的随伴現象説の追加命題

前述のように、$${O_i}$$が非量子論的であり、かつ$${O_i}$$と$${O_\epsilon}$$の相互作用が非量子論的であれば、物理値の経路$${\{P_i(\tau)\}_{t_0 \le \tau}}$$及び$${\{P_\epsilon(\tau)\}_{t_0 \le \tau}}$$を考えることができ、それが意識が随伴するための方程式$${\mathcal{M}_\lambda P_i = 0 }$$を満たすかを考えることができる。そのため、$${O_i}$$が非量子論的であり、かつ$${O_i}$$と$${O_\epsilon}$$の相互作用が非量子論的であることを、随伴現象説を量子論に拡張するにあたって追加で成り立つとする追加命題と呼ぶことにしたい。

物理量を省略することなく記載すると、物理量$${\{ O_\xi\}_ { \xi \in \Lambda \cup E}}$$が全て非量子論的な物理量であり、かつそれらの間の相互作用も非量子論的であるというのが、追加命題となる。

この量子論的随伴現象説の追加命題の意味するところは、繰り返しになるが、$${\{ O_\lambda\}_ { \lambda \in \Lambda }}$$と$${\{ O_ \epsilon\}_ { \epsilon \in E}}$$の固有状態は、時間が経過しても、$${\{ O_ \epsilon\}_ { \epsilon \in E}}$$の固有状態である限り、$${\{ O_\lambda\}_ { \lambda \in \Lambda }}$$の固有状態であるということである。非量子論では、物理量の値は決定論的に変化し、重ね合わせ状態になることはない。これは、量子論の言葉で言えば、固有状態が固有状態であり続けるということである。固有状態であれば、当該物理量についての重ね合わせ状態ではないからである。随伴現象説の基本命題と同等の命題が量子論において成立するためには、その前提として追加命題が成り立つと都合が良い。そのため、本稿の量子論版随伴現象説では、基本命題の前提として追加命題も成り立つと考えることにしたい（筆者は、現段階で追加命題が正しいと主張するつもりはない。単に随伴現象説を量子論に拡張するための最も単純な仮定と考えられるため、一旦採用して考察を進めてみようという主旨である。）。

$${\{ O_\lambda\}_ { \lambda \in \Lambda }}$$は、意識が随伴するという特別な物理量であるから、その固有状態において追加命題が成り立つとしてもそれほどあり得ない想定ということはないだろう。一方で、$${\{ O_ \epsilon\}_ { \epsilon \in E}}$$は任意の状態と相互作用し得るので、$${\{ O_ \epsilon\}_ { \epsilon \in E}}$$の固有状態については、$${\{ O_\lambda\}_ { \lambda \in \Lambda }}$$以外との相互作用で重ね合わせ状態になるとしている（ならないという命題は設定していない。）。時間が進むことにより物理量$${\{ O_ \epsilon\}_ { \epsilon \in E}}$$の値が異なる状態の重ね合わせ状態になった場合は、そのなかから特定の値$${\{ P_\xi\}_ { \xi \in E }}$$の固有状態$${|\{ P_\xi\}_ { \xi \in E} \rangle}$$を抜き出す（固有状態に射影する）ことで、物理量$${\{ O_ \xi\}_ { \xi \in \Lambda}}$$についても固有状態になる。それは追加命題が成り立つとしているからである。その際の$${\{ O_ \xi\}_ { \xi \in \Lambda}}$$の値を$${\{ P_ \xi\}_ { \xi \in \Lambda}}$$としよう。すると、$${\{P_\xi (\tau)\}_{\xi \in \Lambda \cup E , \tau \in \mathbb{R} \ge t_0} }$$という物理値の経路を想定することができる。そして、その経路が、随伴現象説の基本命題の運動方程式$${\forall \lambda \in \Lambda \quad \mathcal{M}_\lambda {\{ P_\xi\}_ { \xi \in \Lambda \cup E }} = 0 }$$を満たすとすると、その経路のそれぞれの点のうち意識が随伴する物理量の値の状態$${|\{ P_ \xi\}_ { \xi \in \Lambda} \rangle}$$には意識が随伴すると考えられる（非量子論の場合に意識が随伴すると考えているのに量子論の場合には随伴しないと考える理由が筆者には思い付かないので随伴すると考えられるという趣旨である。）。すなわち、$${f_S(|\{ P_ \xi\}_ { \xi \in \Lambda} \rangle) \ne \varnothing}$$である。このようにして、随伴現象説は重ね合わせが離散的ではない量子論全般に拡張可能である。

再び射影仮説について

離散的でない重ね合わせの場合の波束の収束について考えよう。再び式を簡易にするために一変数だけとして式を記載する。また、もっとシンプルにするために、$${Q_\epsilon}$$の記載も省略しよう（ただし、量子論全般の場合には前述したように意識を特定するには$${Q_\epsilon}$$が必要なので、記載を省略するだけであるもの思って検討することが必要である。）。すなわち、

$$
\int \! dq \,\, \int \! dQ_i \,\,\Psi (t,Q_i,q)|Q_i\rangle \otimes | q \rangle
$$

の状態において、意識$${f_S(|P_i \rangle ) }$$にとって何が存在して、何が存在しないのかを考える。そのときの存在の意味は、従来と同様に、「存在＝現実と異なる仮想状態を考えた際に私の意識が異なりえる」ということである。

連続の重ね合わせ状態で考えるのはやはり難しいので、意識の状態については離散的な場合を一旦考えよう。まず、時刻$${t_0}$$における状態

$$
\frac{1}{\sqrt{2}} |P_i\rangle \otimes \int \! dq \,\,\Psi (t_0,P_i,q) | q \rangle +  \frac{1}{\sqrt{2}}  |W_i\rangle \otimes \int \! dq \,\, \Psi (t_0,W_i,q)| q \rangle
$$

からの時間進展後の状態を考える。時間進展の作用素$${e^{-\frac{i}{\hbar}H(t-t_0)}}$$を上式にかけた状態を

$$
\int \! dq \,\, \int \! dQ_i \,\,\Psi_P (t,Q_i,q)|Q_i\rangle \otimes | q \rangle + \int \! dq \,\, \int \! dQ_i \,\,\Psi_W (t,Q_i,q)|Q_i\rangle \otimes | q \rangle
$$

とする。ただし、第1項、第2項は、時刻$${t_0}$$における状態の第1項、第2項に作用素$${e^{-\frac{i}{\hbar}H(t-t_0)}}$$をかけたものである。離散的な場合と異なり、これは、

$$
\int \! dq \,\, \int \! dQ_i \,\, ( \Psi_P (t,Q_i,q) + \Psi_W (t,Q_i,q) ) |Q_i\rangle \otimes | q \rangle
$$

と書くこともできる。すなわち、離散的な場合と異なり、$${|P_i\rangle }$$にとって$${\int \! dq \,\, \Psi (t_0,W_i,q)| q \rangle }$$は存在しないのと同じとはいえないということである。こうしたことが起こるのは、$${\Psi_P (t,P_i,q) \ne 0}$$かつ$${\Psi_W (t,P_i,q) \ne 0}$$となる$${P_i}$$が存在するためである。
それでは、随伴現象説を量子論に拡張できたとしても、実験結果を説明するためには、射影仮説が別途必要なのであろうか。その点で鍵を握るのは、意識は記憶を伴っているということである。

意識の一種と考えられるクオリアは、外界の状況により次々と変わる。そして、異なるクオリアを随伴する状態$${|P_i(t_0)\rangle }$$と$${|W_i(t_0)\rangle }$$が時間の経過により同じ状態$${|P_i(t)\rangle }$$になることはありえる。

一方で、記憶を担っている物理量も非量子論的な物理量であり、その値により異なる記憶を持っているとすると、異なる記憶を持ち続けている限り時間の経過により同じ状態になることはない。すなわち、記憶を担う物理量の添字集合を$${\Gamma}$$とすると、$${|\{P_m\}_{m \in \Gamma} \rangle}$$と$${|\{W_m\}_{m \in \Gamma} \rangle}$$が少しでも異なる記憶を持つ状態であれば、$${\exists m \in \Gamma \quad P_m \ne W_m}$$である。

そこで、時刻$${t_0}$$における状態

$$
\frac{1}{\sqrt{2}} |\{P_i\}_{i \in \Lambda \cup \Gamma } \rangle  \otimes \int \! dq \,\,\Psi (t_0,\{P_i\} _{i \in \Lambda \cup \Gamma },q) | q \rangle \\
+  \frac{1}{\sqrt{2}}  |\{W_i \}_{i \in \Lambda \cup \Gamma } \rangle \otimes \int \! dq \,\, \Psi (t_0,\{W_i\} _{i \in \Lambda \cup \Gamma },q)| q \rangle
$$

からの時間進展を考えることにしたい。ただし、今回も物理量$${\{O_\epsilon\}_{\epsilon \in E}}$$の部分系の状態については式が長くなるのを避けるために省略した。上記の式は、ある実験を行い、その結果が$${A}$$と$${B}$$であった状態で、$${|\{P_i\}_{i \in \Lambda \cup \Gamma } \rangle}$$は実験結果が$${A}$$であったとの意識を随伴し、実験結果が$${A}$$であったという記憶を持つ状態だとしよう。状態から随伴する意識への写像$${S}$$に加えて、状態から保持している全ての記憶の集合への写像$${M}$$を導入する。写像$${M}$$を用いると、状態$${|\{P_m\}_{m\in \Gamma } \rangle}$$が実験結果$${A}$$を記憶として保持していることは、$${f_M(|\{P_m\}_{m \in \Gamma } \rangle ) \ni A}$$と書ける。状態$${|\{W_m\}_{m\in \Gamma } \rangle}$$が実験結果$${B}$$を記憶として保持していることは、$${f_M(|\{P_m\}_{m \in \Gamma } \rangle ) \ni B}$$と書ける。時刻$${t_0}$$における状態は、そうした状態だとしよう。

時間進展の作用素$${e^{-\frac{i}{\hbar}H(t-t_0)}}$$を上式にかけた状態を

$$
\int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int \! dQ_i \,\,\Psi_P (t,\{Q_i\},q)|\{Q_i\}\rangle \otimes | q \rangle \\
+ \int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int \! dQ_i \,\,\Psi_W (t,\{Q_i\},q)|\{Q_i\}\rangle \otimes | q \rangle
$$

としよう。前回同様に、第1項、第2項は、時刻$${t_0}$$における状態の第1項、第2項に作用素$${e^{-\frac{i}{\hbar}H(t-t_0)}}$$をかけたものである。これまた前回同様に、上式は、

$$
\int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int \! dQ_i \,\,（ \Psi_P (t,\{Q_i\},q) + \Psi_W (t,\{Q_i\},q) ) |\{Q_i\}\rangle \otimes | q \rangle
$$

と書くことができるが、前回とは異なるところがある。それは、時刻$${t \gt t_0}$$においても実験結果の記憶が保持されているとすると、$${\Psi_P (t,\{Q_i\},q) }$$か$${ \Psi_W (t,\{Q_i\},q) }$$のいずれかは$${0}$$であるということである。すなわち、

$$
\forall \{Q_i\}_{ i \in \Lambda \cup \Gamma} \quad \Psi_P (t,\{Q_i\},q)  \Psi_W (t,\{Q_i\},q) = 0
$$

である。起こっている現象を見通しやすくするために、

$$
\Psi (t,\{Q_i\},q) = \Psi_P (t,\{Q_i\},q) + \Psi_W (t,\{Q_i\},q)
$$

として、時刻$${t}$$における状態を

$$
\int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int_{\{\{Q_i\}_{i \in \Lambda \cup \Gamma} | f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni A\}} \! \! \! dQ_i \,\,\Psi(t,\{Q_i\},q)|\{Q_i\}\rangle \otimes | q \rangle \\
+ \int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int _{ \{\{Q_i\}_{i \in \Lambda \cup \Gamma}  | f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni B\}} \! \! \! \! dQ_i \,\,\Psi (t,\{Q_i\},q)|\{Q_i\}\rangle \otimes | q \rangle
$$

と書き直そう。ここで、積分記号の下に記載した$${ \{\{Q_i\}_{i \in \Lambda \cup \Gamma}  | \, f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni A\}}$$は、当該集合に含まれる$${ \{Q_i\}_{i \in \Lambda \cup \Gamma} }$$についてのみ積分するという意味である。ここでのポイントは、2つの項の積分範囲に交わりがないということである。言い換えると、積集合が空集合であるということであり、式で書くと

$$
\{\{Q_i\}_{i \in \Lambda \cup \Gamma}  | \, f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni A\} \cap \{\{Q_i\}_{i \in \Lambda \cup \Gamma}  | \, f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni B\}  =  \varnothing
$$

である。

$${A}$$の記憶をともなう意識にとって何が存在しないのと同じかどうかを考えるために、時刻$${t}$$における状態の第2項を変更した下記の状態

$$
\int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int_{\{\{Q_i\}_{i \in \Lambda \cup \Gamma} | f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni A\}} \! \! \! dQ_i \,\,\Psi_P(t,\{Q_i\},q)|\{Q_i\}\rangle \otimes | q \rangle \\
+ \int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int _{ \{\{Q_i\}_{i \in \Lambda \cup \Gamma}  | f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni B\}} \! \! \! \! dQ_i \,\,\Psi_W^{\prime} (t,\{Q_i\},q)|\{Q_i\}\rangle \otimes | q \rangle
$$

から時間進展した（$${e^{-\frac{i}{\hbar}H(\tau-t)}}$$をかけた）状態

$$
\int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int_{\{\{Q_i\}_{i \in \Lambda \cup \Gamma} | f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni A\}} \! \! \! dQ_i \,\,\Psi_P^{\prime}(\tau, \{Q_i\}, q)|\{Q_i\}\rangle \otimes | q \rangle \\
+ \int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int _{ \{\{Q_i\}_{i \in \Lambda \cup \Gamma}  | f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni B\}} \! \! \! \! dQ_i \,\,\Psi_W^{\prime} (\tau, \{Q_i\}, q)|\{Q_i\}\rangle \otimes | q \rangle
$$

を考える。そうすると、

$$
\Psi_P^{\prime}(\tau, \{Q_i\}_{i \in \Lambda \cup \Gamma}  , q) = \Psi_P(\tau, \{Q_i\}_{i \in \Lambda \cup \Gamma}  , q)
$$

となる。それは、時間が経過しても、$${\Psi_W^{\prime} (\tau, \{Q_i\}_{i \in \Lambda \cup \Gamma}, q) \ne 0 \land f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni A\ }$$ となることはないからである。これは、記憶を保持する物理量$${\{O_m\}_{m \in \Gamma}}$$の値が満たす運動方程式が極めて特殊なためである（より正確には、物理量$${\{O_m\}_{m \in \Gamma}}$$がとりえる全ての値においてではなく、一定の範囲内の値においてと考えられる。）。

このようにして、$${A}$$の記憶を伴う意識にとって、状態の第2項、時刻$${t_0}$$においては、

$$
\frac{1}{\sqrt{2}}  |\{W_i \}_{i \in \Lambda \cup \Gamma } \rangle \otimes \int \! dq \,\, \Psi (t_0,\{W_i\} _{i \in \Lambda \cup \Gamma },q)| q \rangle
$$

は存在しないのと同じであるといえる（万人が合意するとは思われないが、筆者は存在しないのと同じといえると考える。）。すなわち、意識が認識する実験結果には射影が起こっている。随伴現象説による記憶を伴う意識を検討範囲に含めれば、量子力学の実験結果を説明するために、射影仮説は不要ということである。

無限個の実験結果がある場合

前節では、実験結果が$${A}$$と$${B}$$の2つの場合のみを考えたが、これは容易に実験結果が複数の場合に拡張できる。無限個の実験結果がある場合にも拡張可能である。実験結果を$${A_1,A_2,\cdots}$$とすると、状態は、

$$
\sum_{k=1}^\infty \int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int_{\{\{Q_i\}_{i \in \Lambda \cup \Gamma} | f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni A_k\}} \! \! \! dQ_i \,\,\Psi(t,\{Q_i\},q)|\{Q_i\}\rangle \otimes | q \rangle
$$

と書ける。そして、$${A_j}$$を測定したという意識にとっては、

$$
\sum_{k \in \mathbb{N} \setminus \{j\}} \int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int_{\{\{Q_i\}_{i \in \Lambda \cup \Gamma} | f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni A_k\}} \! \! \! dQ_i \,\,\Psi(t,\{Q_i\},q)|\{Q_i\}\rangle \otimes | q \rangle
$$

は存在しないのと同じである。

$$
\sum_{k \in \mathfrak{P}(\mathbb{N} \setminus \{j\})} \int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int_{\{\{Q_i\}_{i \in \Lambda \cup \Gamma} | f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni A_k\}} \! \! \! dQ_i \,\,\Psi(t,\{Q_i\},q)|\{Q_i\}\rangle \otimes | q \rangle
$$

も存在しないのと同じである。ただし、$${\mathfrak{P}(\mathbb{N} \setminus \{j\})}$$は$${\mathbb{N} \setminus \{j\}}$$の冪集合であり、$${\mathfrak{P}(\mathbb{N} \setminus \{j\}) = \{B | \, B \subseteq \mathbb{N} \setminus \{j\}\}}$$である。

実験結果が連続固有値をとる物理量の値の場合も同様に考えることができ、物理値$${v \in \mathbb{R}}$$を測定したことを$${A_v}$$と書くことにすると、状態は

$$
\int \! d\nu \,\, \int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int_{\{\{Q_i\}_{i \in \Lambda \cup \Gamma} | f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni A_\nu \}} \! \! \! dQ_i \,\,\Psi(t,\{Q_i\},q)|\{Q_i\}\rangle \otimes | q \rangle
$$

と書ける。そして、$${A_v}$$を測定したという意識にとっては、$${v_1 \lt v_2 \lt v \lt v_3 \lt v_4}$$とすると、

$$
\int_{v_1}^{v2} \! d\nu \,\, \int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int_{\{\{Q_i\}_{i \in \Lambda \cup \Gamma} | f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni A_\nu \}} \! \! \! dQ_i \,\,\Psi(t,\{Q_i\},q)|\{Q_i\}\rangle \otimes | q \rangle \\
+ \int_{v_3}^{v4} \! d\nu \,\, \int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int_{\{\{Q_i\}_{i \in \Lambda \cup \Gamma} | f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni A_\nu \}} \! \! \! dQ_i \,\,\Psi(t,\{Q_i\},q)|\{Q_i\}\rangle \otimes | q \rangle
$$

は存在しないのと同じである。また、

$$
\int_{-\infty}^{v_2} \! d\nu \,\, \int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int_{\{\{Q_i\}_{i \in \Lambda \cup \Gamma} | f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni A_\nu \}} \! \! \! dQ_i \,\,\Psi(t,\{Q_i\},q)|\{Q_i\}\rangle \otimes | q \rangle \\
+ \int_{v_3}^{\infty} \! d\nu \,\, \int \! dq \,\, \prod_{i \in \Lambda \cup \Gamma} \int_{\{\{Q_i\}_{i \in \Lambda \cup \Gamma} | f_M(|\{Q_m\}_{m \in \Gamma } \rangle ) \ni A_\nu \}} \! \! \! dQ_i \,\,\Psi(t,\{Q_i\},q)|\{Q_i\}\rangle \otimes | q \rangle
$$

も存在しないのと同じである。$${v_2}$$と$${v_3}$$は、十分に（どこまでも）$${v}$$に近づけることができるため、意識が認識する実験結果には連続固有値の場合にも射影が起こっているといえる。このように、随伴現象説による記憶を伴う意識を検討範囲に含めれば、量子力学の実験結果を説明するために、射影仮説は不要ということである。

まとめ

連続的な重ね合わせ状態で意識を随伴する部分系が複数存在する場合の考察、ボルンの規則の考察等、考察するべきことはまだ多く残っているが、すでに分量も多くなったことから、ここで筆を置くことにしたい。

ここまでで述べてきたように、随伴現象説は量子論に拡大できる可能性が十分にあり、記憶を伴う意識の随伴現象説を量子論に拡大できれば、射影仮説のない量子論の公理系において、実験結果を説明することができるようになると筆者は考える。

これは単に、射影仮説を随伴現象説仮説でおきかえるということであるが、筆者にとって、射影仮説・コペンハーゲン解釈が奇妙な説であるのに対して、随伴現象説は筆者にとって特段奇妙でない説であるので、射影仮説を随伴現象説仮説で置き換えることができれば、心がやすらぎ、観測問題は問題ではないと感じることができる。

追記

追記1: 科学と哲学

冒頭に「哲学なので、筆者には特に奇異ではなく（ありえるだろう）と思われることをそれほどの根拠なく述べるものである。」と書いたが、私が言いたかったことを含むとてもよくまとまったnoteを見つけたので、リンクしておきたい。「理系の哲学嫌いもこのパターンが多いように思えます」、「哲学は科学のような強力な共通認識を生み出すことができません。議論の対象に客観的な要素が少なすぎるからです」などが冒頭の内容を記載した理由で下記の記事に賛同するところです。