
【量子コンピュータ基礎4】量子テレポーテーション
今回は、量子テレポーテーションについて解説したいと思います。
量子テレポーテーションとは、何らかの量子情報(量子状態)を相手に届ける手法です。例えば下の図の場合、田中さんから山田さんに対して、$${\ket{\psi}}$$という量子情報を送るといったようなことです。

おそらく、「テレポーテーション」と聞くと、多くの人がSF映画でよくみるような、人や物が一瞬にして移動する現象を想像する方が多いかもしれません。しかし残念ながら、現実世界の量子テレポーテーションでは、物質や人を転送することはできません。そのかわり、量子状態を移動させることができるのです。
量子情報はコピーできない: No-cloning定理
結局量子テレポーテーションとは、何らかの量子情報を送るというものでした。でも単純に情報を送るのであれば、送りたい情報をコピーして、それを送ればいいのではないでしょうか。現実社会でも、適当な記憶媒体にデータをコピーして渡したりしますよね。これを同じように量子情報にたいしても行えばいいのではないでしょうか。

しかし結論から答えると、量子情報をコピーしてまったく同じ状態を作ることはNo-cloning定理によって禁止されています。(No-cloning定理の証明は、最後のおまけのセクションに載せておきます。)


量子テレポーテーション
それでは、量子情報を相手に届けたい時には、どうすればいいのでしょうか。これを実現する一つの手法が、量子テレポーテーションです。詳しく見ていきましょう。量子テレポーテーションとは、エンタングル状態にある量子ビットを共有している者同士の間で、とある量子状態
$$
\ket{\psi}=\alpha\ket{0}+\beta\ket{1}
$$
を送信する技術です。それではどのようにして量子テレポーテーションを実現するのかをみていきましょう。例のごとく、田中さんから遠隔地にいる山田さんに対して量子情報$${\ket{\psi}}$$を送るという状況を考えてみます。こちらが、田中さんと山田さんとの間で、量子テレポーテーションを実現する量子回路になります。

Step1: 初期状態
初期状態として、田中さんと山田さんの量子ビットがそれぞれ$${\ket{0}}$$に初期化されています。

つまり初期状態は、
$$
\ket{\Psi_1}=\ket{\psi}\ket{0}_t\ket{0}_y
$$
と記述できます。
Step2: エンタングル状態の共有
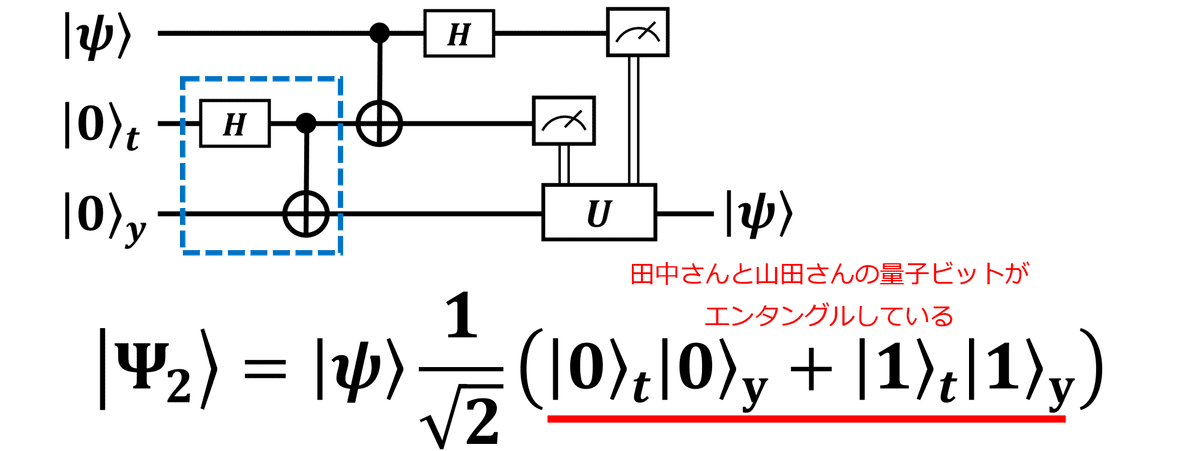
次に、田中さんと山田さんの間でエンタングル状態の共有を行います。量子回路では、田中さんの量子ビットにアダマールゲートを与え、田中さんと山田さんの量子ビット間にCNOTゲートをかけます。すると、
$$
\ket{\Psi_2}=\ket{\psi}\frac{1}{\sqrt{2}}(\ket{0}_t\ket{0}_y+\ket{1}_t\ket{1}_y)=(\alpha\ket{0}+\beta\ket{1})\frac{1}{\sqrt{2}}(\ket{0}_t\ket{0}_y+\ket{1}_t\ket{1}_y)
$$
$$
\frac{1}{\sqrt{2}}(\alpha\ket{0}\ket{0}_t\ket{0}_y+\alpha\ket{0}\ket{1}_t\ket{1}_y+\beta\ket{1}\ket{0}_t\ket{0}_y+\beta\ket{1}\ket{1}_t\ket{1}_y)
$$
となります。
Step3: CNOTゲートとアダマールゲート
次に、CNOTゲートとHadamardゲートを与えます。すると、

と記述できます。さて、この量子状態について見てみましょう。よく見ると、第一項に、送りたい量子情報
$$
\ket{\psi}=\alpha\ket{0}+\beta\ket{1}
$$
が含まれています。また、第二項に関しては、
$$
\alpha\ket{1}_y+\beta\ket{0}_y
$$
という部分があります。この状態は、$${X}$$ゲートを操作させると、
$$
X(\alpha\ket{1}_y+\beta\ket{0}_y)=\alpha\ket{0}_y+\beta\ket{1}_y=\ket{\psi}
$$
となり、送りたい量子情報と一致しますね。また、第三項と第四項に関しては、それぞれ$${Z}$$ゲートと$${Y}$$ゲートを作用させることで$${\ket{\psi}}$$が得られます。つまり、適切な作用を与えることで、送りたい量子状態を手に言えれることができそうな感じがしますね。

Step4: 田中さん側での量子ビットの測定し結果を山田さんへ伝達
次に、田中さん側で量子ビットの測定を行います。

そして、その結果を山田さんに伝えます。その測定結果に応じて、以下のような量子状態を得ることができます。

Step5: 測定結果に応じて量子ビットを操作
最後に、測定結果に応じて得られた量子状態に対して適切な操作を与えます。

例えば、$${\ket{0}\ket{0}_t}$$という測定結果が得られた場合は、結果として$${\ket{\psi}}$$と同じ量子状態が得られるので、何もしません。$${\ket{0}\ket{1}_t}$$という測定結果が得られた場合は、$${X}$$ゲートを作用させることで、$${\ket{\psi}}$$と同じ量子状態が得られます。同様にして、その他の結果が得られた場合にも、適切な量子ゲートを作用させることで、送りたかった量子情報を得ることができます。このようにして量子テレポーテーションが実現できるのです。
おまけ: No-cloning定理の証明
No-cloning定理とは、任意の量子状態$${\ket{\psi}}$$のコピーの生成を原理的に禁止する定理です。この定理を確かめてみましょう。
とある量子状態$${\ket{\psi}}$$のコピーを作ることを考えます。これを数式で表すことを考えます。ここで、$${\ket{\psi}}$$という状態と、なにも書き込まれていない量子ビット$${\ket{0}}$$を用意します。
$$
\ket{\psi}\ket{0}
$$
そして、$${\ket{\psi}}$$のコピーを何も書き込まれていない二つ目の量子ビットに作ることを考えます。すると、この操作によって、
$$
\ket{\psi}\ket{\psi}
$$
という量子状態が生成されます。もう少し、数式的にこの操作を定式化すると、なんらかのコピーを作る操作$U$を用いて、以下のように記述できます。
$$
U\ket{\psi}\ket{0}=\ket{\psi}\ket{\psi}
$$
ここで、異なる量子ビット$${\ket{\phi}}$$に対してもこの操作を与えることを考えます。すると、以下のように記述できます。
$$
U\ket{\phi}\ket{0}=\ket{\phi}\ket{\phi}
$$
ここで、上記の式の内積を考えます。まず左辺に関しては、
$$
UU^\dagger=I
$$
なので、$${\braket{\psi|\phi}}$$となります。また、右辺に関しては、$$
{\braket{\psi|\phi})^2}$$となります。つまり、
$$
\braket{\psi|\phi}=(\braket{\psi|\phi})^2
$$
が成り立つことととなります。つまり、この式が成り立つということは、
$$
\braket{\psi|\phi}=0, 1
$$
となりますが、これは任意の量子状態である、$${\ket{\psi}}$$と$${\ket{\phi}}$$が同一または直行しているということを意味しています。しかしこの結果は、$${\ket{\psi}}$$と$${\ket{\phi}}$$が任意の量子状態であるという仮定に反しています。このことから、任意の量子状態をコピーするような操作$${U}$$というものは存在しないという結論になります。
(こちらの記事は、以前Qiitaに投稿した内容の書き直しです。)
