
ポケモン対戦:情報アドがある状態での択ゲーについてその1
要約
ポケモン対戦の2×2の択ゲーについて、型がわからない時の計算を行い勝率と最適な選択比率をを計算しました。型をわからなくすることにより型バレ時と比較して勝率が$${\frac1{p}}$$になることがわかりました。これは非常に大きい数字であり、ポケモン対戦における型バレの有無の重要性がわかります。
始めに
ポケモン対戦において情報というのは非常に重要な意味を持っており、型バレがあるかないかで対戦の有利不利が大きく変わります。今回はこのような情報の有無に関して、友人から面白い問題を教えてもらったのでゲーム理論使って考えてみようという記事です。
問題設定
友人にもらった問題設定は以下のようになっています。
相手:
マルスケ切れたカイリューとドオー テラス残ってない
自分:
ドオーの地震でもワンパン圏内の電気テラス切ったパオジアン
カイリューの地震ワンパン圏内のメガネカミ
ただしサイコショックは見せてない
カミVSカイリュー対面
居座りならムンフォで勝ち
交代ならショックで勝ち 逆は負け どっち押しますか?
2×2の選択問題と考えるとよくある問題設定です。しかし、サイコショックを見せていないことによる情報アドバンテージがこちらの選択や勝率にどう影響を与えるか考えると面白い問題になってきそうです。
まずサイコショックがバレている場合をまとめると次のようになります。〇がこちらの勝ち、×が相手の勝ちです。

一方、サイコショックがあることがバレていない場合は相手視点では次の1×2問題と上の2×2問題のどちらになっているかがわからない状態になっています。

相手視点で2×2問題になっている確率を$${p}$$と書くことにします。
計算
計算にあたっての注意
なお、今回の内容は不完備情報ゲームという枠組みで、正しい計算方法を後になって知ったのですが、記事を書き始めた時は知らずに手探りで考えていたため説明の文章がやや正しくないかもしれません。出てくる方程式自体やその解き方は正しいこと確認したので、なぜその方程式を解けばいいのかの説明が違う感じになっていても大目に見てください。
解き方に関してはこちらの動画を参考にさせていただきました。ちゃんとした説明や解き方を知りたい方はリンク先の動画や他の専門書で勉強してください。
また計算の際、相手視点で考えることが何度かあります。相手の勝率とこちらの勝率が混ざっているとややこしいので相手視点考えている時でも勝率はこちらの勝率で考えます。
サイコショック持ちだとわかっている場合
まずはサイコショックがあることがバレている時のゲーム理論の標準的な計算方法について解説します。
こっちがどう選ぶかは本来相手にはわからないのですが、ゲーム理論でムズカシイ事ごちゃごちゃやると、こちらが何%で技を選ぶかが相手にバレてる想定で確率計算した時の結果を使えばいいことがわかるそうです。(だいぶ不正確に要約してます。詳しく知りたい方はミニマックス定理で検索お願いします。)
というわけでこちらがムンフォやショックを打つ確率がバレてる前提で計算します。
こちらがショック打つ確率をxとすると相手視点では
交代:確率xでこちらの勝ち
居座り:確率1-xでこちらの勝ち
となるので相手視点$${x>1-x}$$だと居座りを選択し、$${x<1-x}$$だと交代を選択します。 まとめるとxを色々変えた時のこちらの勝率は$${x}$$と$${1-x}$$の小さい方がこちらの勝率になります。
$$
勝率=\min(x,1-x)
$$
min(x,1-x)のグラフは↓のようになるのでx=50%、つまりショックとムンフォを50%ずつで選択するのが勝率が一番高くなってベストという結果になります
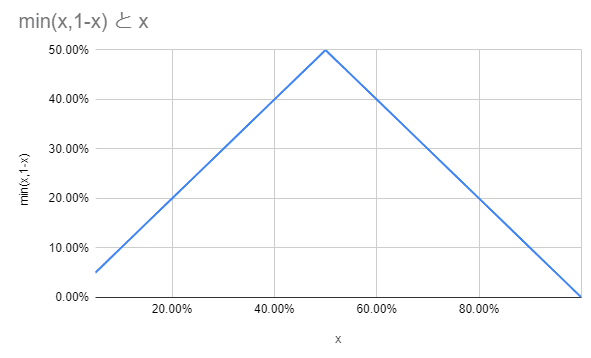
まとめるとこちらはムーンフォース50%サイコショック50%で出すのがベストで、この時こちらの勝率は50%になります。
ここまでがこちらがサイコショック持ちなのを相手も理解してる時の理論です。相手視点でこちらがサイコショックを持ってるかどうかわからない時にここからどう変わっていくかを考えたいというのが今回の目的になります。
サイコショック持ちかわからない場合
この場合カイリュー側はこちらがサイコショックを持っているかどうかわからないため、サイコショックを持っているかどうかまで考えてこちらが勝ちにくくなる選択をする必要があります。
相手視点でこちらがサイコショックを持っている確率を$${p}$$とします。サイコショックを持っている時にショックを打つ確率を$${x}$$とすると相手視点で交代と居座りの勝率はそれぞれ次のようになります。
交代:確率pxでこちらの勝ち
居座り:確率p(1-x)+(1-p)でこちらの勝ち
相手はこちらの勝率がもっとも低くなるように交代と居座りの比率を決めます。$${px=p(1-x)+1-p}$$を満たす$${x}$$を$${x_0}$$と置くと、相手は$${x< x_0}$$なら交代、$${x>x_0}$$なら居座りを選択することになります。
$${x_0}$$を求めると以下の様になります。
$$
px_0=p(1-x_0)+1-p\\
2px_0=1\\
x_0=\frac1{2p}
$$
したがって相手視点でこちらの勝率は次のようになります。
$$
勝率=\{ \begin{array}{cc}px&x< x_0=\frac1{2p}\\
1-px &x > x_0=\frac1{2p}
\end{array}
$$
また$${p}$$が50%以下になると$${x_0}$$が$${x}$$の動ける範囲(0%~100%)に入りきらなくなります。すると右肩上がりのグラフになるので勝率が最大になる$${x}$$は$${x=100\%}$$となります。
まとめると勝率が最大となるような$${x}$$の時、$${勝率=px=\max(px_0,100\%\times p)=\max(50\%, p)}$$となります。
こちら視点ではサイコショックを持っていることが確定しているので勝率は次のようになります。
$$
勝率=\{ \begin{array}{cc}x&x<\frac1{2p}\\
1-x &x>\frac1{2p}
\end{array}
$$
上の結果を図示すると次のようになります。
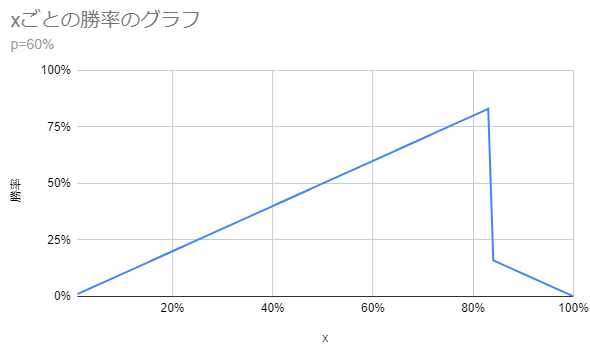
勝率が最大になるのは$${x=x_0}$$の点に下側から近づけた時なので勝率は$${x_0=\frac{1}{2p}}$$です。また、先ほどと同様に$${x_0}$$がグラフの範囲に入りきらない場合は$${x}$$や勝率が100%になります。
まとめ・考察
まとめると次のようになります。
サイコショックカミの最適なサイコショックの選択確率:$${\max(\frac{1}{2p},100\%)}$$
サイコショックカミの勝率:$${\max(\frac{1}{2p},100\%)}$$
カイリュー側から見て、カミがサイコショックを持っていてかつそれを選ぶ確率:$${\max(50\%,p)}$$
つまりサイコショック持ちがバレている時は勝率50%だった勝率が、型の匿名性により勝率を増やすことができます。具体的には$${50\%→50\%×\frac1p}$$とサイコショックを持っている確率の逆数の分だけ勝率が向上し、$${p}$$が50%に到達した時点で100%に達します。
あとがき
いかがでしたか?
型がバレてない状態では勝率が上がることがわかりました。この事自体は当たり前といえばそうなのですが、今回型バレ時の1/pになるという定量性をもって示せたことは一つの面白い結果なのかなと思います。
勝率の増え方の程度も$${p=50\%}$$と半分混ざった時点で勝率が100%まで届くレベルと、非常に影響が大きい事もわかります。マイナー好きとしてはガンガン変な型使っていきたいと思います。
この記事が気に入ったらサポートをしてみませんか?
