
ポケモン:構築の組み方理論その2
こんにちは。先日の記事の改良版です。その1↓と合わせてご覧ください。
要約
ポケモン間の相性関係を線でつなぐことで表すことにし、図形にして表すことで構築の中の関係性を表現しました。そして、自分のポケモン同士の相性の良さの他に相手による強さの変動を考慮したモデルで全ての図形について計算を行うことで最も強い図形を求めました。結果、前回と同様に一匹のポケモンを中心にしたパーティが強いという結論が得られました。
始めに
ポケモン対戦において構築の組み方は重要です。補完の良さや起点を必要とするなどの理由で相性の良い組み合わせが存在します。しかし6匹中どのポケモンも相性が良くなるように構築を組むことは困難です。構築に入れられる相性の良い組み合わせの総数は限られている中でどのポケモンとどのポケモンの相性を重視して組めば良いでしょうか?前回から簡単なモデルを組んで調査を行っていました。
ポケモンを点で表し、相性の良い組み合わせでは点と点の間に線を引くことでパーティ内の関係性を表現することにします。

前回は選出パターン数を構築の強さの指標として様々な図形について強さの計算を行い、強い図形を探しました。
前回の問題点として単純に選出パターンの数をそのまま構築の強さとして定義していたため、選出パターンこそ多いが全部の選出に同じポケモンが入っていて選出の幅が狭くなっているような構築でも強い構築であるという結果が出てしまいそうな実験になっていました。
今回は構築の強さの決め方をもう少し深く考えていきたいと思います。
そもそも選出パターンが多い方が良いというのは、相手パーティに通りが悪いポケモンがいた時に通りが良いポケモンを多く使った選出パターンを採用しやすいのが原因です。このことを直接的に数式に取り入れてみます。
相手パーティによってそれぞれのポケモンの通りが良い時と悪い時があるわけなので、それを再現するためにポケモンの強さがランダムに変動するとします。そしてその変動やポケモン間の相性により一番強くなった選出を行うと考え、最も強い選出の強さにより構築の強さを定義します。
これにより1人のポケモンに強く依存したパーティはそのポケモンの通りが悪い時に強い選出ができにくくなり、構築の強さも低くなるはずです。
方法
具体的な計算手順は以下になります。
まず、個々のポケモンの強さを0~1の間でランダムに決め、選出の強さを次で定義します。$${α}$$を乱数の影響の強さを表すパラメータにします。
$${選出の強さ=α×個々の強さの和+(1-α)×ポケモン間の直線の数}$$$${_6C_3=20}$$通りの選出パターンがありますが、その全てについて選出の強さを計算し、最も強い選出の数字を記録します。
以上を10000回繰り返し最も強い選出の強さを平均します。
前回の作り方で出来る図形は以下の6パターンあるのでそれぞれについて1.~3.の計算を行います。

乱数で個々のポケモンの通りの良さが変動する効果とポケモン同士の相性の強さがそれぞれどれくらいの比率になっているかによって結果が変わる可能性があります。そのためパラメータ$${\alpha}$$を導入して乱数の効果と相性の効果の比率を調整できるようにしました。$${\alpha=0}$$の時は完全に相性の良さだけで選出の強さが決まるようになり、$${\alpha=1}$$の時は完全に個々のポケモンの通りの良さだけで選出の強さが決まります。
結果
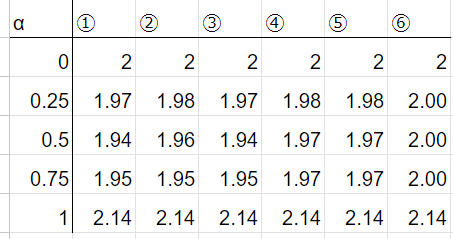
計算を行い、構築の強さを表にしました。結果は以下のようになりました。表の数字が大きい図形ほど強い構築であることを表しています。

考察
パラメータの大きさに関わらず⑥>④⑤>②>①③という傾向があることがわかります。つまり、相手パーティによる通りの良さの変動を考慮して計算し、一匹に依存したパーティが不利になるような計算を行ったとしても⑥のように一匹を中心とした構築が強いという結果になりました。
なぜこのような結果になったのでしょうか?
⑥のように一匹を中心にした構築は中心以外のポケモンを自由に選べることから選出パターンが多いことがわかっています。中心のポケモンが不利な相手では通りの悪いポケモンを選出しなければならないデメリットを他のポケモンを自由に選べることによる上振れが上回った結果今回の結果になったと考えられます。
まとめ
相手に合わせてそれぞれのポケモンの通りの良さを変動させる条件で計算を行うことで、一匹のポケモンに依存しすぎるとそのポケモンが通らなかった時に一気に不利になる現象を考慮しました。
その上でも一匹を中心に相性が良いポケモンをまとめる構築が他の構築より強くなるという結果が得られました。
あとがき
いかがでしたか?今回は通りの良さによる強さの変動を考慮してその構築の中で一番強い選出の強さにより構築の強さを定義してみました。
単純に選出パターンの数のみで評価した前回と比較して一匹に依存したパーティにはかなり逆風になるような計算条件だったと思いますが、それにもかかわらず一匹中心のパーティが強いという結果が出ました。個人的にはかなり意外で、ここまで不利な計算条件なら前回と異なる結果が出ると思っていましたが、この条件においても強いならちゃんと実戦でも強い事が期待できそうです。
この記事が気に入ったらサポートをしてみませんか?
