正規分布をノイズとして利用するためのメモ

1. このメモに書かれていること

・データdに±e程度の誤差を与えるための正規分布N(d, σ)における標準偏差σの求め方(第2章)

・データdに確率pで大きさe未満の誤差を与えるための正規分布N(d,σ)における標準偏差σの求め方(第3章)

2. データdに±e程度の誤差を与えるための正規分布N(d, σ)における標準偏差σの求め方

N(d, σ)に従う確率変数Dの期待値は、正規分布の性質よりdである。
これは、σによらず、期待値としては誤差が乗らないことを意味している。

これでは議論にならないため、Dでなく|D-d|の期待値を計算しよう。これは誤差D-dの絶対値であるため、|D-d|の期待値E[|D-d|]とは、「誤差の大きさの期待値」であるといえる。故にE[|D-d|]=eとなればよい。

まず、Dｰd (~ N(0,σ))の確率密度関数は次の通り。

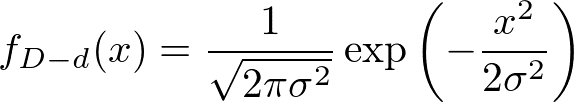
Dｰdの値が「だいたいx」と定まる確率は、上の式に比例するのである。
この式はx=0に対して対称、すなわち偶関数だ。
故に「だいたいx」と定まる確率は「だいたい-x」と定まる確率に等しい。
それなら次のように考えてもよさそうではないか。

「D-dの値はまず絶対値が確率密度関数f_{|D-d|}に従って定まり、それから正負が同様に確からしく定まることによって決まる。」

f_{|D-d|}は次のようになる。

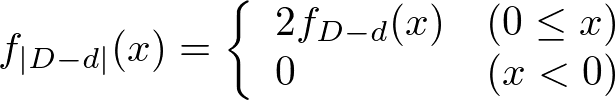
2をかけているのは、「実数全体における定積分値(面積)を1に保つ」ためである。面積のうちの半分を0にしたため、その埋め合わせを行っている。

さらに、次のようにかける。

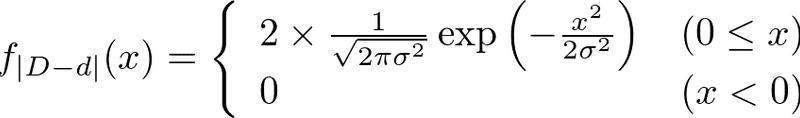
さて、以上のような分布における期待値はいったいいくつになるだろうか。

連続確率変数Xの期待値E[X]を確率密度関数から計算する公式は次の通り。

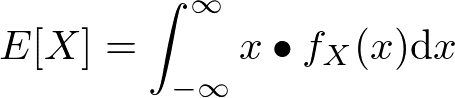
これに当てはめ、計算すると

=e
(参考: https://ai-trend.jp/basic-study/normal-distribution/n-parameter-derivation/)

故に、期待値eの誤差を乗せるための正規分布の標準偏差σは

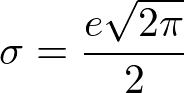
である。

2-1. pythonを用いた検証

正規分布N(d, {e√(2π)}/2)に従う確率変数Xから値をとる試行を何回か行い、
|x-d|の平均値がeに近づくことを確かめよう。

pythonコードは次の通り。

import numpy as np

N = np.random.normal 

def dとeから確率変数(d,e): # 関数を返すメタ関数
    def myfunction(cnt=1): # 確率変数の値を返す関数
        return N(d,e*np.sqrt(2*np.pi)/2, cnt) # N(d, {e√(2π)}/2)
    return myfunction # 「確率変数の値を返す関数」を返す

X = dとeから確率変数(1998, 912) 
# 1998に±912程度の誤差を乗せるような正規分布に従う確率変数X

data = X(1000000) # Xの値xをとる試行1000000回 

print("試行1~10の結果は次の通り。")
print(data[0:10]) # 10回目までの値を表示

print("\nxの平均値は次の通り。(約1998)")
print(np.average(data)) # xの平均値(≒Xの期待値≒1998)

print("\n|x-d|の平均値は次の通り。(約912)")
print(np.average(np.abs(data-1998))) #|x-d|の平均値(≒912)

結果は次の通りになった。

試行1~10の結果は次の通り。
[ 901.86541638 3088.23730139 1520.83743621 3110.08930079 2677.53603518
1438.97293774 -987.08589708 1584.61119675 1240.60131598 2326.16732553]

xの平均値は次の通り。(約1998)
1998.5961800715818

|x-d|の平均値は次の通り。(約912)
911.5111723650343

まあだいたいこんなもんだろう。誤差率を計算させたいなら次の通り。

誤差率 = lambda 測定値,真値: print(str(100*abs(測定値-真値)/真値)+"%")

誤差率(1998.5961800715818, 1998) # 0.029838842421510733%
誤差率(911.5111723650343,  912)  # 0.053599521377815075%

3. データdに確率pで大きさe未満の誤差を与えるための正規分布N(d,σ)における標準偏差σの求め方

累積分布関数F_X(x)とは、その分布に従う確率関数Xがx以下に定まる確率を返す関数であった。

例えば

だった場合、Xは半分の確率で負の値になる。
故に、

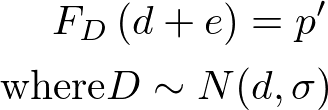
といえるとき、「確率p'でDはd+e以下になる」といえる。
但しこれは「ノイズの大きさがe以下になる確率がp'」ということではない。
何故なら、d-e未満の値になる(つまりノイズが-eより小さい(絶対値はeより大きい))場合がp'には含まれてしまっているからだ。
まず、ノイズが負になる場合を除くと、確率が0.5だけ下がることから、
「Dがd以上d+e以下に定まる確率はp'-0.5」といえる。
正規分布の確率密度関数が偶関数であることから、
「『Dがd-e以上d+e以下』つまり『誤差の大きさがe以下』に定まる確率は2p'-1=p」といえる。
2p'-1=pを整理するとp'=(1/2)(p+1)
さらにX := D-dとして

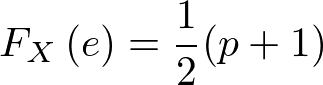
という式が立てられる。・・・①
正規分布N(μ,σ)においては、累積分布関数は

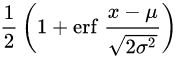
であるから、X ~ N(0, σ)に対しては

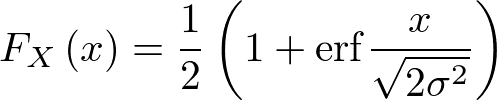
・・・②
よって、x=eとして①＝②とすれば

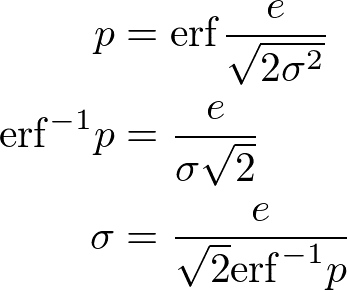
3-1. pythonを用いた検証

pythonのライブラリscipyではerfの逆関数を計算することが出来る。
そこで、eとpを適当に決めてσを計算し、そのσにて本当に誤差の大きさe未満の確率がpとなるかどうかを確認するためのコードを示す。(結果は面倒なので省略)

pythonコードは次の通り。

from sympy import erfinv, sqrt
import numpy as np

       
N = np.random.normal 

def dとeとpから確率変数(d,e,p): # 関数を返すメタ関数
   def myfunction(cnt=1): # 確率変数の値を返す関数
       return N(d,e/(sqrt(2)*erfinv(p)), cnt) # N(d, e/(√2)erfinv(p))
   return myfunction # 「確率変数の値を返す関数」を返す

with open("research.csv", "w") as f:
   f.write("e,p,誤差率[%],実測rate[%]\n")
   for e in [0.000001, 1, 10000000]:
       for p in np.array(range(1,100))/100:
           X = dとeとpから確率変数(0, e, p)
           x = X(100000000)
           rate = np.count_nonzero(np.abs(x)<e)/100000000
           err = np.abs(rate-p)/p
           print("e="+str(e)+", p="+str(p)+"のとき、誤差率"+str(100*err)+"%、実測rate"+str(100*rate)+"%")
           f.write(str(e)+","+str(p)+","+str(100*err)+","+str(100*rate)+"\n")