
PieceCHECK(2024-18) 絶対値付き方程式の解の個数
いつもご覧いただきまして、ありがとうございます。KATSUYAです。
【最新巻】『数学A~図形の性質~』『数学B・C~統計的な推測~』販売開始!!
まもなく割引期間終了します!!まだの方はぜひ^^
1つの問題から、多くの問題が出来るようになるための考え方・手法(原則:Principle)を出来る限り分かりやすく、そして詳しく言葉に落とし込んだ数学の問題集です。
単元自体を未習の方も、本シリーズで最初から体系的に高校数学を学べます。そして、学習後の到達レベルは「難関大入試合格最低点レベル」です!
今回の問題
YouTube動画をUPしました。今回は富山大から、絶対値付き方程式の解の個数に関する問題です。
思考時間は約5分、目標解答時間はそこから20分です。
解説・原則など
今回は絶対値付き2次関数のグラフを書き、後半でさらに複雑な絶対値付きの方程式の解の個数を求める問題。
(1)のグラフはいいでしょう。全体に絶対値が付いているので、$${x}$$軸より下を来るっとひっくり返せばOK。
(2)は定数$${a}$$の入った方程式の解の個数です。もちろんこちらの原則を適用することは思いつくと思います。
文字定数入りの方程式の解の個数は定数分離で視覚化
ただ今回は、$${a}$$だけを分離するのはかなり難しいので、(1)のグラフを書いた意味も最大限にいかして、
$${\bm{|x^2-2x-3|-a}=\pm2}$$
として、$${\bm{y=\pm2}}$$との共有点の個数の合計を見ていくのが分かりやすかったと思います。
そうすれば、左辺も(1)のグラフを上下に動かすだけです。あとは$${a}$$を少しずつ動かしながら、共有点を慎重に調べます。場合分けは多いですが、やさしい数値設定のおかげでまだマシです。
絶対値を外さずに、$${y=||x^2-2x-3|-a|}$$と$${y=2}$$の共有点としてもいいですが、そうすると前者の方はかなり複雑なグラフになりますので、もっと時間がかかると思います。
一応こちらの解法でもやってみました+こう解いた人も結構いると思いますので、載せておきますね。(こちらが解1です)
1.解けた人・・・今後の勉強はじっくり演習をしましょう。
2.解けなくて原則を知っていた人・・・拙著『Principle Piece』シリーズで該当するページを熟読し(詳細が書いてあります)、入試演習用の問題集で思考時間を長くする演習をしましょう。
3.解けなくて原則も知らなかった人・・・原則集めからやる必要があります。拙著『Principle Piece』シリーズのような原則習得タイプの問題集で演習しましょう。
関連する拙著『Principle Piece』シリーズ
Principle Piece シリーズは、1つの問題から、多くの問題が出来るようになるための考え方・手法(原則:Principle)によって、「なぜその解法が思い浮かぶのか」「なぜ解答の1行目がそれになるのか」を意識して書き上げた参考書です。
大手ネットショップBASEでも、デジタルコンテンツとして販売しています。
解答
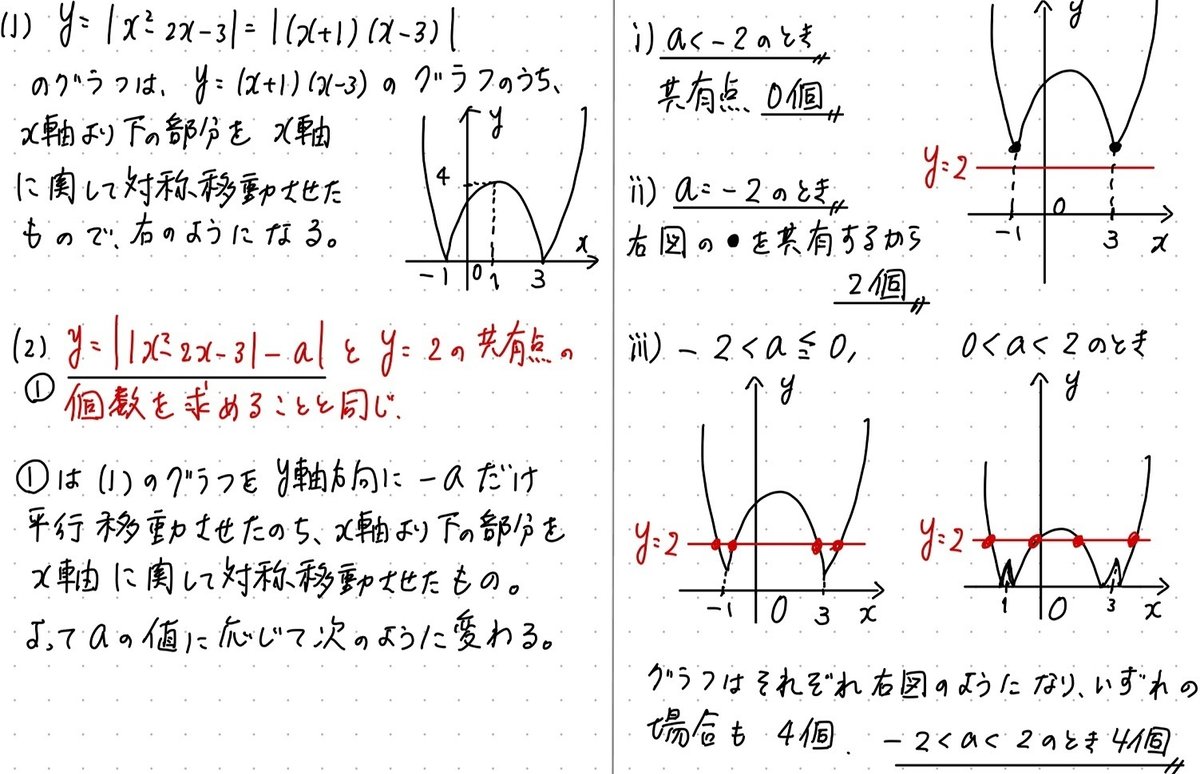


※ここより先には内容はございません。本記事に価値を感じていただけた方は、ポチっとしていただけると大変うれしいです。(もちろん、任意です)
ここから先は
¥ 100
この記事が気に入ったらサポートをしてみませんか?
