PieceCHECK(2023-26) 方程式の実数解条件

いつもご覧いただきまして、ありがとうございます。KATSUYAです。

お知らせ

拙著シリーズ『Principle Piece 数学B・C～平面ベクトル～』
拙著シリーズ『Principle Piece 数学B・C～空間ベクトル～』
同時販売開始しました！(23/05/29)

今回の問題

YouTube動画をUPしました。今回は中部大学からで、方程式が実数解を持つ条件です。

思考時間は12分、目標解答時間はそこから約10分です。

こちらの記事では、動画の中で紹介した解説(答え)を少し丁寧にした答案を、静止画像にて掲載しておきます。

解答

解説・原則など

ルート付きの方程式が実数解を持つ条件です。いろいろな解法が考えられます。

解１は2乗して根号をなくし、2次方程式の解の存在範囲に帰着させる方法です。ただし、単純に2乗すると同値関係が崩れるので、こちらの原則を意識しましょう。

根号を含む方程式では、根号の中身も根号の式も0以上

詳細は拙著シリーズ『Principle Piece数学B～平面ベクトル～』p.23を参照

これに注意して変形していくと、結局$${x\geqq  a}$$の範囲で異なる2つ実数解を持てばよいことになります。これはパターンですね。

解の存在範囲は「D、軸、端っこ」の(符号の)調査

詳細は拙著シリーズ『Principle Piece数学Ⅰ～２次関数～』p.72を参照

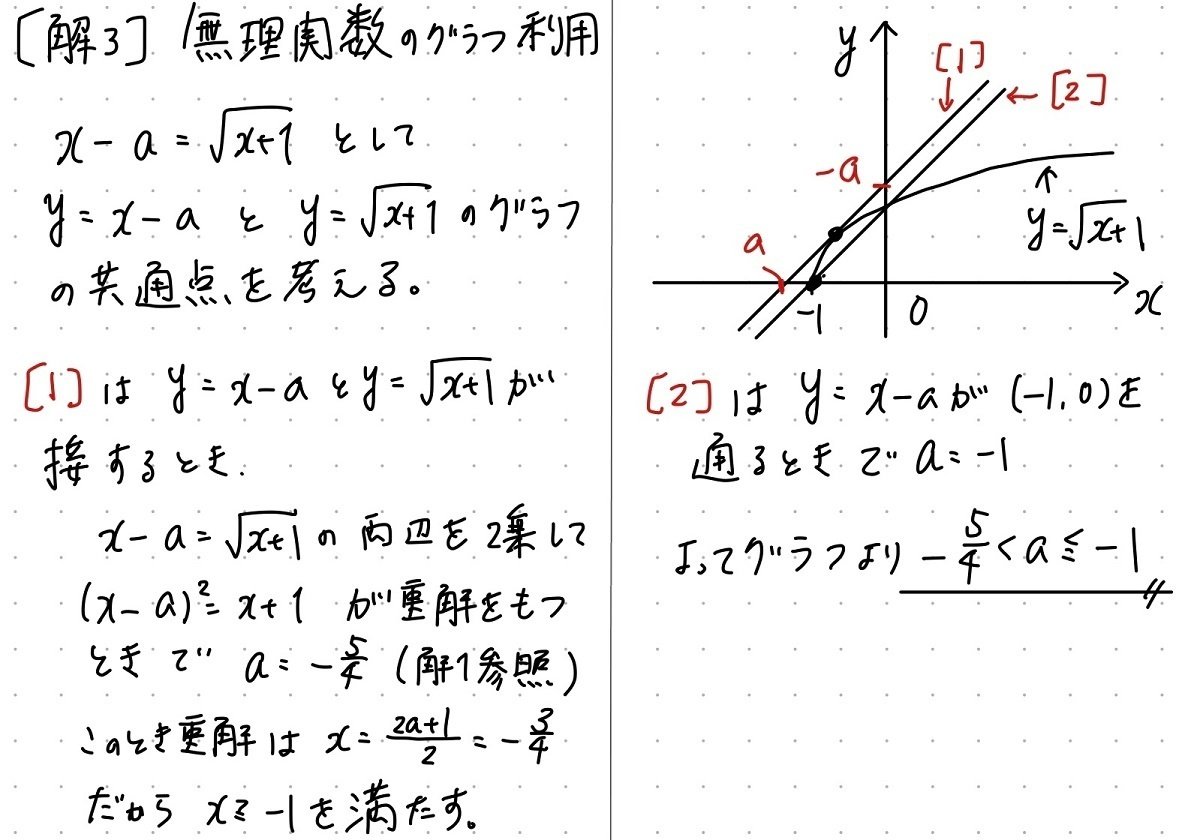
解２は、定番のグラフによる視覚化です。こちらの原則を思い出しましょう。

文字定数入りの方程式の解の個数は定数分離で視覚化

詳細は拙著シリーズ『Principle Piece数学Ⅰ～２次関数～』p.82を参照

定数分離という言葉がセットで使われる視覚化ですが、それはグラフを書きやすいようにする目安にすぎません。グラフが書きやすいように分離すればOK。
今回は2乗して$${(x-a)^2=x+1}$$とすれば、どちらもグラフは視覚化しやすいですね。

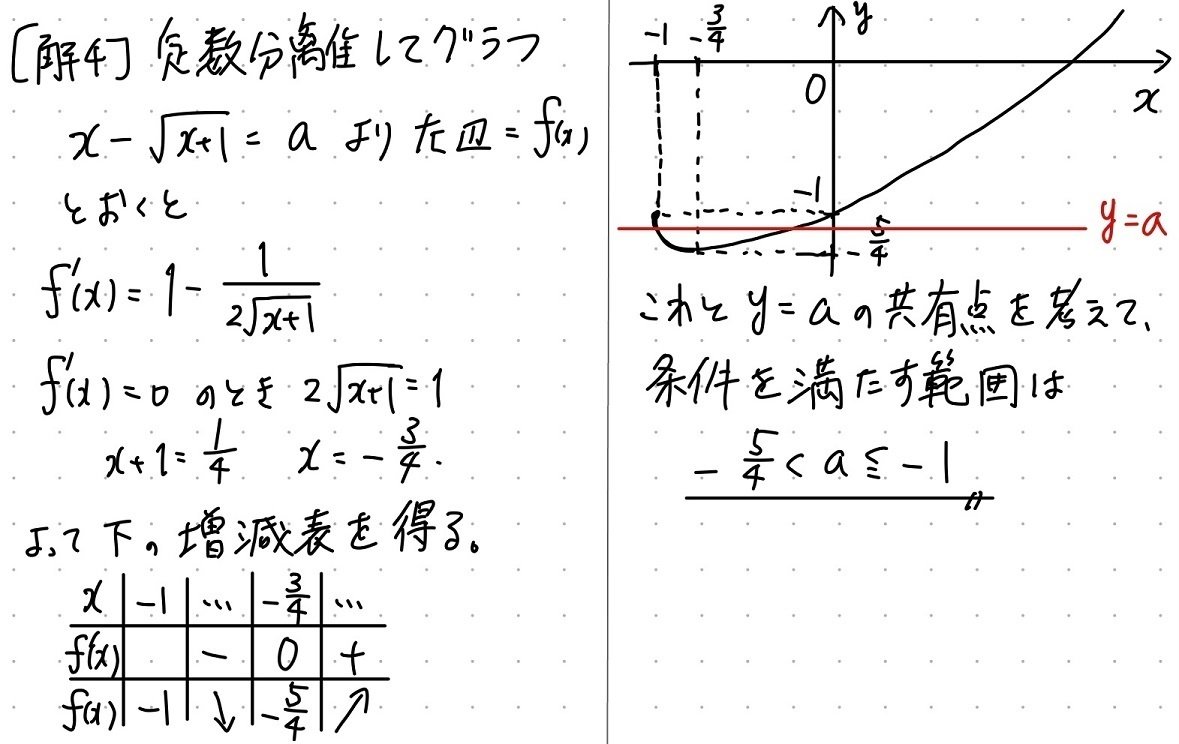
解３、解４は数IIIの知識を使った視覚化です。$${\sqrt{x+1}=x-a}$$とするか、もうそのまま左辺を微分してグラフを書くかです。工学部での出題ですので、もしこれしか思い浮かばないのなら、これでやればOKでしょう。

本番中は様々な解法で勉強する時間ではなく、時間内に出来る限り点数を稼ぐ時間です。思いついた方法でやればOK。

１．解けた人・・・今後の勉強はじっくり演習をしましょう。

２．解けなくて原則を知っていた人・・・拙著『Principle Piece』シリーズで該当するページを熟読し(詳細が書いてあります)、入試演習用の問題集で思考時間を長くする演習をしましょう。

３．解けなくて原則も知らなかった人・・・原則集めからやる必要があります。拙著『Principle Piece』シリーズのような原則習得タイプの問題集で演習しましょう。

Piece CHECKシリーズは、出来あがった答案からは見えない部分を解説していくことで、「なぜそうやって解くのか」「いったいどこからそんな答案が生まれるのか」が分かることを意識して書き上げた参考書です。

関連する拙著『Principle Piece』シリーズ

解の存在範囲のパターンについてはかなり体系的に紹介しています＾＾

※根号付きの方程式の原則ついては、こちらの本で説明しています↑

principle powered by BASE

大手ネットショップBASEでも、デジタルコンテンツとして販売しています。

※ここより先には内容はございません。本記事に価値を感じていただけた方は、ポチっとしていただけると大変うれしいです。(もちろん、任意です)