フーリエ解析をやってみよう!
すしすきーのまとも代表(笑)ポテト君です!
そしてこれは すしすきーアドベントカレンダー2023 20日目の記事です
みんな大好きポテト君の算数の時間だよ!みんな集まれ〜!
ということで今日は小学生のみんなに
フーリエ解析
について教えるよ!
みんな微積分は覚えてるかな?もちろん大丈夫だよね!
フーリエ級数展開
まずはフーリエ級数展開を見ていくよ
簡単に言うと、周期的な関数を定数関数と三角関数で表すことだよ!
前提として以下の条件を満たすよ
周期が$${2\pi}$$の関数である(すなわち$${f(x)=f(x+2\pi)}$$)
区分的になめらかな関数である
$${f}$$が区分的になめらか
→$${f}$$の微分が存在し、$${f,f'}$$どちらも区分的に連続であること
区分的に連続
→連続または有限個の第一種の不連続点を除き連続
点aで連続
→$${\lim_{x→a}f(x)=f(a)}$$
極限の厳密な定義はε-δ論法より
$${\forall ε>0 \exists δ>0 s.t. \forall x\in \mathbb R [0<|x-a|<δ\Rightarrow |f(x)-b|<ε]}$$
このとき$${\lim_{x→a}f(x)=b}$$と定義する
区間Iで連続
→I上のすべての点で連続
第一種の不連続点
→右側極限及び左側極限が存在し、発散しない(一致する必要はない)
このとき
$${f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty (a_n\cos(nx)+b_n\sin(nx))}$$
とすることを考えるよ($${\{a\},\{b\}は定数列}$$)
厳密には=が成り立つのはf(x)に第一種の不連続点を含まないときのみである
これを$${-\pi→\pi}$$で積分すると
$${\int_{-\pi}^{\pi}f(x)dx=\int_{-\pi}^{\pi}\frac{a_0}{2}dx+\int_{-\pi}^{\pi}\sum_{n=1}^\infty (a_n\cos(nx)+b_n\sin(nx))dx}$$
項別積分可能である条件は一様収束であることだが、区分的になめらかな関数は一様収束することが知られているので
$${\int_{-\pi}^{\pi}f(x)dx=\int_{-\pi}^{\pi}\frac{a_0}{2}dx+\sum_{n=1}^\infty (\int_{-\pi}^{\pi}a_n\cos(nx)dx+\int_{-\pi}^{\pi}b_n\sin(nx)dx)}$$
$${\int_{-\pi}^{\pi}f(x)dx=a_0\pi}$$
$${a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx}$$
また、両辺に$${\cos(ix)\, (i\in\mathbb N_+)}$$をかけると同様に
$${\int_{-\pi}^{\pi}f(x)\cos(ix)dx=\int_{-\pi}^{\pi}\frac{a_0}{2}\cos(ix)dx+\sum_{n=1}^\infty (\int_{-\pi}^{\pi}a_n\cos(nx)\cos(ix)dx+\int_{-\pi}^{\pi}b_n\sin(nx)\cos(ix)dx)}$$
$${\int_{-\pi}^{\pi}f(x)\cos(ix)dx=\pi a_i}$$
$${a_i=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(ix)dx}$$
$${\sin(ix)}$$をかけて
$${\int_{-\pi}^{\pi}f(x)\sin(ix)dx=\int_{-\pi}^{\pi}\frac{a_0}{2}\sin(ix)dx+\sum_{n=1}^\infty (\int_{-\pi}^{\pi}a_n\cos(nx)\sin(ix)dx+\int_{-\pi}^{\pi}b_n\sin(nx)\sin(ix)dx)}$$
$${\int_{-\pi}^{\pi}f(x)\sin(ix)dx=\pi b_i}$$
$${b_i=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin(ix)dx}$$
これでフーリエ級数展開の公式が得られたよ!
(不連続点では右側極限と左側極限の算術平均を取る)
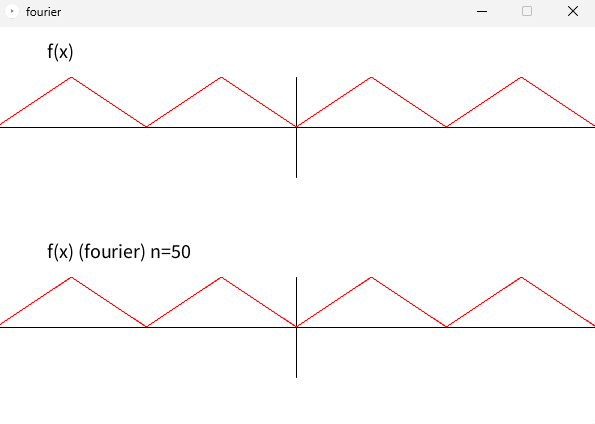
試しにのこぎり波をフーリエ級数展開した例をあげるよ!

ちなみにLaTeXで書いてすしでノートしたやつだよ
これをプログラミングで描画してみるよ!
使うのはProcessing
ソースコードは
float f(float x){
if(x<=-PI)return abs(x-2*int((int(x/PI)-1)/2)*PI);
return abs(x-2*int((int(x/PI)+1)/2)*PI);
}
float a_n(int n){
if(n==0)return PI;
if(n%2==0)return 0;
return -4/PI/n/n;
}
float b_n(int n){
return 0;
}
float f_fourier(float x,int nMax){
float sum=a_n(0)/2;
for(int n=1;n<nMax;n++){
sum+=a_n(n)*cos(n*x)+b_n(n)*sin(n*x);
}
return sum;
}
void setup(){
size(600,400);
textSize(20);
}
int fourier_n=50; //nの最大値
void draw(){
noLoop();
background(255);
pushMatrix();
translate(300,100);
stroke(0);
line(-300,0,300,0);
line(0,50,0,-50);
fill(0);
text("f(x)",-250,-70);
stroke(255,0,0);
float start[]={-4*PI,f(-4*PI)};
for(float x=-4*PI;x<4*PI;x+=8*PI/600){
line(start[0]*300/PI/4,-start[1]*50/PI,x*300/PI/4,-f(x)*50/PI);
start[0]=x;
start[1]=f(x);
}
popMatrix();
pushMatrix();
translate(300,300);
stroke(0);
line(-300,0,300,0);
line(0,50,0,-50);
fill(0);
text("f(x) (fourier) n="+str(fourier_n),-250,-70);
stroke(255,0,0);
start[0]=-4*PI;
start[1]=f_fourier(-4*PI,fourier_n);
for(float x=-4*PI;x<4*PI;x+=8*PI/600){
line(start[0]*300/PI/4,-start[1]*50/PI,x*300/PI/4,-f_fourier(x,fourier_n)*50/PI);
start[0]=x;
start[1]=f_fourier(x,fourier_n);
}
popMatrix();
}これを実行すると
また2lの周期関数では
$${f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty (a_n\cos(\frac{n\pi x}{l})+b_n\sin(\frac{n\pi x}{l}))}$$
$${a_0=\frac{1}{l}\int_{-l}^{l}f(x)dx}$$
$${a_n=\frac{1}{l}\int_{-l}^{l}f(x)\cos(\frac{n\pi x}{l})dx}$$
$${b_n=\frac{1}{l}\int_{-l}^{l}f(x)\sin(\frac{n\pi x}{l})dx}$$
になるよ
複素フーリエ級数展開
オイラーの公式は覚えてるかな?はい!お前君!
「$${e^{i\theta}=\cos\theta+i\sin\theta}$$のことです!」
その通り!
ここからフーリエ級数の式をうまく変形できないか考えていくよ
オイラーの公式から
$${\cos\theta=\frac{e^{i\theta}+e^{-i\theta}}{2}}$$
$${\sin\theta=\frac{ie^{-i\theta}-ie^{i\theta}}{2}}$$
だから
$${a_n\cos(nx)+b_n\sin(nx)}$$
$${=a_n\frac{e^{inx}+e^{-inx}}{2}+b_n\frac{ie^{-inx}-ie^{inx}}{2}}$$
$${=\frac{a_n-ib_n}{2}e^{inx}+\frac{a_n+ib_n}{2}e^{-inx}}$$
ここで$${c_n=\frac{a_n-ib_n}{2}}$$と定義する
$${c_n}$$のnが負になった場合を考えると、$${b_n}$$のみ$${\sin nx}$$の符号が逆になる
よって
$${c_{-n}=\frac{a_n+ib_n}{2}}$$
また$${n=0}$$を考えると、$${b_0}$$が0で消えて
$${c_0=\frac{a_0}{2}}$$
これで
$${f(x)=\sum_{-\infty}^{\infty}c_ne^{inx}}$$
$${c_n={a_n-ib_n}{2}=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)e^{-inx}dx}$$
になることが分かるよ!
フーリエ級数のプログラムの関数f_fourierを
float f_fourier(float x,int nMax){
float sum=0;
for(int n=-nMax;n<nMax;n++){
sum+=a_n(n)*cos(n*x)/2+b_n(n)*sin(n*x);
}
return sum;
}にすると同じ結果を得ることができるよ!
複素フーリエ級数では範囲が2lのとき
$${f(x)=\sum_{-\infty}^{\infty}c_ne^{\frac{in\pi x}{l}}}$$
$${c_n=\frac{1}{2l}\int_{-l}^{l}f(x)e^{-\frac{in\pi x}{l}}}$$
になる
フーリエ変換
複素フーリエ展開を$${(-\infty,\infty)}$$の範囲に拡張→周期性のない関数でもフーリエ展開を行えるようにするよ!
関数の条件は
絶対可積分である
区分的に連続である
絶対可積分
→$${\int_{-\infty}^{\infty}|f(x)|dx}$$が$${\infty}$$に発散しない
複素フーリエ展開の式を変形してみるよ
$${f(x)=\sum_{n=-\infty}^{\infty}(\frac{1}{2l}\int_{-l}^{l}f(t)\exp(\frac{-in\pi t}{l})dt\exp(\frac{in\pi x}{l}))}$$
$${\tau_n=\frac{n\pi}{l},\Delta\tau=\tau_{n+1}-\tau_n=\frac{\pi}{l}}$$とすると
$${=\sum_{n=-\infty}^{\infty}((\frac{1}{2\pi}\int_{-l}^{l}f(t)e^{-i\tau_n t}dte^{i\tau_n x})\Delta\tau)}$$
ここで$${l\rightarrow\infty}$$とすれば
$${\Delta\tau\rightarrow 0}$$で、$${\tau_n}$$はすべての実数を取る
これはリーマン積分になるので
$${f(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(t)e^{-i\tau(t-x)}dtd\tau}$$
これはフーリエ積分公式と言うよ!
フーリエ積分公式を
$${\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(t)e^{-i\tau t}dte^{i\tau x}d\tau}$$
として、中の部分を取り出した
$${\mathcal{F}[f(x)](\tau):=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(t)e^{-i\tau t}dt}$$
をフーリエ変換という(複素フーリエ級数でいう$${c_n}$$と対応する)
その外
$${\mathcal{F}^{-1}[F(\tau)](x):=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}F(\tau)e^{i\tau x}d\tau}$$
をフーリエ逆変換というよ!(複素フーリエ級数と対応)
これはもちろん
$${\mathcal{F}^{-1}[\mathcal{F}[f(x)](\tau)](x)=f(x)}$$
が成り立つ
じゃあこれをProcessingで確かめていくよ!
ここでは台形公式の数値積分を使うよ
具体的には
$${a\rightarrow b}$$で$${h}$$間隔で分割してそれぞれを台形で近似した面積$${\frac{h}{2}(f(x_n)+f(x_{n+1}))}$$を足していくことで近似する方法のこと
ソースコード全体は
float f(float x){
return exp(-x*x);
}
float f_fourier(float x,int nMax){
float sum=0;
for(float i=-nMax;i<nMax;i+=0.1){
float sum_in[][]={{0,0},{0,0}};
for(float j=-nMax;j<nMax;j+=0.1){
for(int k=0;k<2;k++){
sum_in[k][0]+=0.1*(f(j)*cos(-j*(i+0.1*k))+f(j+0.1)*cos(-(j+0.1)*(i+0.1*k)))/sqrt(2*PI)/2;
sum_in[k][1]+=0.1*(f(j)*sin(-j*(i+0.1*k))+f(j+0.1)*sin(-(j+0.1)*(i+0.1*k)))/sqrt(2*PI)/2;
}
}
sum+=0.1*(sum_in[0][0]*cos(i*x)-sum_in[0][1]*sin(i*x)+sum_in[1][0]*cos((i+0.1)*x)-sum_in[1][1]*sin((i+0.1)*x))/sqrt(2*PI)/2;
}
return sum;
}
void setup(){
size(600,400);
textSize(20);
}
int fourier_n=3;
void draw(){
noLoop();
background(255);
pushMatrix();
translate(300,100);
stroke(0);
line(-300,0,300,0);
line(0,50,0,-50);
fill(0);
text("f(x)",-250,-70);
stroke(255,0,0);
float start[]={-4*PI,f(-4*PI)};
for(float x=-4*PI;x<4*PI;x+=8*PI/600){
line(start[0]*300/PI/4,-start[1]*50/PI,x*300/PI/4,-f(x)*50/PI);
start[0]=x;
start[1]=f(x);
}
popMatrix();
pushMatrix();
translate(300,300);
stroke(0);
line(-300,0,300,0);
line(0,50,0,-50);
fill(0);
text("f(x) (fourier) n="+str(fourier_n),-250,-70);
stroke(255,0,0);
start[0]=-4*PI;
start[1]=f_fourier(-4*PI,fourier_n);
for(float x=-4*PI;x<4*PI;x+=8*PI/600){
line(start[0]*300/PI/4,-start[1]*50/PI,x*300/PI/4,-f_fourier(x,fourier_n)*50/PI);
start[0]=x;
start[1]=f_fourier(x,fourier_n);
}
popMatrix();
}実行すると

ちゃんと元の関数が得られてるのが分かるね!
ラプラス変換
フーリエ変換を絶対可積分でない関数についても行えるように工夫したものがラプラス変換だよ!
例えば1や$${x}$$,$${\sin x}$$,$${\cos x}$$といった多くの関数は絶対可積分ではないね
ここで$${x<0}$$では$${f(x)=0}$$と定義して$${e^{-cx}\,(c\in\mathbb{R})}$$をかけることで$${x}$$が大きくなるほど減衰していくようにするよ
ラプラス変換は
$${\mathcal{L}[f(t)](s):=\sqrt{2\pi}\mathcal{F}[e^{-cx}f(x)](\tau)}$$
と定義される($${s:=c+i\tau}$$)
これを変形すると
$${\mathcal{L}[f(t)](s)=\int_{0}^{\infty}(e^{-ct}f(t))e^{-i\tau t}dt}$$
$${=\int_0^{\infty}f(t)e^{-st}dt}$$
ラプラス変換は$${e^{-cx}f(x)}$$が絶対可積分であるような範囲で定義されるから$${c=\text{Re}(s)}$$には下限が一意に定まり、これを収束座標というよ
ラプラス逆変換は
$${\mathcal{L}^{-1}[F(s)]=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}F(s)e^{st}ds}$$
だけどあまり使うことはないよ
よく使われるものを書いておくよ($${x<0}$$で$${f(x)=0}$$であることに注意)
$${\mathcal{L}[1]=\frac{1}{s},収束座標0}$$
$${\mathcal{L}[t]=\frac{1}{s^2},収束座標0}$$
$${\mathcal{L}[t^{n-1}](n=1,2,…)=\frac{(n-1)!}{s^n},収束座標0}$$
$${\mathcal{L}[e^{at}]=\frac{1}{s-a},収束座標\text{Re}(a)}$$
$${\mathcal{L}[\cos at]=\frac{s}{s^2+a^2},収束座標0}$$
$${\mathcal{L}[\sin at]=\frac{a}{s^2+a^2},収束座標0}$$
$${\mathcal{L}[\cosh at]=\frac{s}{s^2-a^2},収束座標|a|}$$
$${\mathcal{L}[\sinh at]=\frac{a}{s^2-a^2},収束座標|a|}$$
$${\mathcal{L}[\frac{1}{\sqrt{t}}]=\sqrt{\frac{\pi}{s}},収束座標0}$$
ラプラス変換の性質も見ていくよ
線形則
$${\mathcal{L}[\alpha f(t)+\beta g(t)]=\alpha\mathcal{L}[f(t)]+\beta\mathcal{L}[g(t)]}$$
相似則
$${\mathcal{L}[f(\lambda t)]=\frac{1}{\lambda}\mathcal{L}[f(t)](\frac{s}{\lambda})}$$
微分則
$${\mathcal{L}[f^{(n)}(t)]=s^n\mathcal{L}[f(t)]-\sum_{k=1}^n\lim_{t\rightarrow +0}f^{(k-1)}(t)s^{n-k}}$$
$${\mathcal{L}^{-1}[\frac{d^n}{ds^n}\mathcal{L}[f(t)]]=(-t)^nf(t)}$$
これもProcessingで確認していくよ!
float f(float x){
if(x<0)return 0;
return sin(x);
}
float f_laplace(float x,int nMax){
if(x<=0)return 0;
float sum=0;
for(float i=0;i<nMax;i+=0.1){
sum+=0.1*(f(i)*exp(-x*i)+f(i+0.1)*exp(-x*(i+0.1)))/2;
}
return sum;
}
void setup(){
size(600,400);
textSize(20);
}
int fourier_n=100;
void draw(){
noLoop();
background(255);
pushMatrix();
translate(300,100);
stroke(0);
line(-300,0,300,0);
line(0,50,0,-50);
fill(0);
text("f(x)",-250,-70);
stroke(255,0,0);
float start[]={-4*PI,f(-4*PI)};
for(float x=-4*PI;x<4*PI;x+=8*PI/600){
line(start[0]*300/PI/4,-start[1]*50/PI,x*300/PI/4,-f(x)*50/PI);
start[0]=x;
start[1]=f(x);
}
popMatrix();
pushMatrix();
translate(300,300);
stroke(0);
line(-300,0,300,0);
line(0,50,0,-50);
fill(0);
text("f(x) (laplace) n="+str(fourier_n),-250,-70);
stroke(255,0,0);
start[0]=-4*PI;
start[1]=f_laplace(-4*PI,fourier_n);
for(float x=-4*PI;x<4*PI;x+=8*PI/600){
line(start[0]*300/PI/4,-start[1]*50/PI,x*300/PI/4,-f_laplace(x,fourier_n)*50/PI);
start[0]=x;
start[1]=f_laplace(x,fourier_n);
}
popMatrix();
}
(sは実数とする)
フーリエ級数展開の応用
周期関数を使用してx,y座標を指定することで図形を描くことができるよ!
たとえば四角形を表示したいなら

として、1辺の長さが1とすれば$${f(t)}$$は

$${g(t)}$$は

$${f(x)$$はフーリエ級数展開のところで計算したのこぎり波を$${F(x)}$$とすれば
$${f(x)=\frac{\sqrt{2}}{\pi}(F(x)-\frac{\pi}{2})}$$
$${g(x)=f(x+\frac{pi}{2})}$$
これを表示すれば

また回転行列

を使えば、これを45°回転して

みたいにできるよ!
他にも
$${F(0)=0=\frac{\pi}{2}-\frac{4}{\pi}\sum_{n=1}^{\infty}\frac{1}{(2n-1)^2}}$$
から
$${\sum_{n=1}^{\infty}\frac{1}{(2n-1)^2}=\frac{\pi^2}{8}}$$
になることが分かるよ
ラプラス変換の応用
ラプラス変換は微分方程式や積分方程式でよく使われるよ!
例えば
$${\frac{d^2x}{dt^2}=-a^2x}$$
$${x(0)=1,\frac{dx}{dt}(0)=a}$$
は公式から解けば
$${x=A\cos t+B\sin t}$$だから
$${x=\cos at+\sin at}$$
だが、ラプラス変換を使って
$${X=\mathcal{L}[x]}$$として両辺をラプラス変換して
$${s^2X-s-a=-a^2X}$$
$${(s^2+a^2)X=s+a}$$
$${X=\frac{s}{s^2+a^2}+\frac{a}{s^2+a^2}}$$
$${x=\mathcal{L}^{-1}[X]=\cos at+\sin at}$$
というように解くこともできるよ
電気回路の解析で使うこともあるよ

十分充電した後にt=0でスイッチを上げたとき
$${v_C(0)=-E,v_R(0)=E,I_C(0)=-\frac{E}{R},I_R(0)=\frac{E}{R}}$$
$${q=Cvよりi_C=-C\frac{dv_C}{dt}}$$
$${I_R=\frac{v_R}{R}=-\frac{v_C}{R}}$$
$${I_C+I_R=0}$$
$${-C\frac{dv_C}{dt}-\frac{v_C}{R}=0}$$
ここでラプラス変換をして
$${CVs+E+\frac{V}{R}=0}$$
$${V=-E\frac{1}{s+1/RC}}$$
$${v_C=-E\exp(-\frac{t}{RC})}$$
$${v_R=E\exp(-\frac{t}{RC})}$$
$${I_C=-\frac{E}{R}\exp(-\frac{t}{RC})}$$
$${I_R=\frac{E}{R}\exp(-\frac{t}{RC})}$$
これはわざわざラプラス変換使わないでも解けるけどね
ということで!みんなもフーリエ解析やってみてね!
この記事が気に入ったらサポートをしてみませんか?
