埃が風に舞う

　エクセルは表計算ソフトというより、シミュレーション・ソフトです。ここでは「埃が風に舞い、積もる」様子をモデル化して、エクセルでシミュレーションします。多少複雑ですが、アレンジして使えばいろんな場面で使える考え方です。

埃が風に舞う

　埃は部屋の隅にたまるものです。部屋の中ほどにも埃はいくらか積りますが、部屋の隅の方が多いですね。
　ところで、なぜ埃は部屋の隅にたまるのでしょうか？　その訳は、部屋の中ほどは窓からの風が通ったり人が歩いたりして比較的強い風が吹いて埃が動きやすいのに対して、部屋の隅では風が弱くて埃があまり動かないからではないでしょうか。以上のことをモデル化して、この現象をエクセルで再現してみましょう。
　まずは話をシンプルにするために、埃１個で、また平面ではなく数直線上を動くものとしてやってみてください。

　モデル化のコツは、最初はなるべくシンプルなモデルを立てることです。そしてそれがうまくいったら、より複雑なモデルを立てればいいのです。いきなり複雑な、リアリティーのあるものを作ろうとしてもたぶん無理です、無駄です、無謀です。
　ここでは話をシンプルにするために、まず埃１つだけで考えましょう。また、平面ではなく、数直線の -1 と +1 の間を埃が動くと考えます。0 の位置が部屋の真ん中で、-1 と +1 の位置が部屋の隅という想定です。
　これくらい条件をシンプルにすれば、なんとかなるでしょうか。さて、次の問題は「この埃をどうやって動かすか」です。

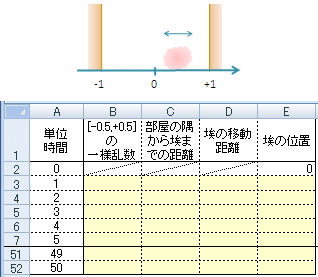
　まず「+0.5 から -0.5 までの一様な乱数」…① を、不規則な風に見立てましょう。このとき、左向きの風はマイナスで、右向きの風はプラスで表されています。
　次に、その値を部屋の中ほどでは強く、部屋の隅では弱くなるように調整しましょう。そのために「部屋の隅から埃までの距離」…② を表す式を作ります。
　そして①と②を掛けた値を「埃の移動距離」…③ とすれば、「部屋の中ほどでは比較的強く、部屋の隅では比較的弱い不規則な風に乗って移動する埃」がモデル化できます。
　さらに直前の「埃の位置」に③を足した値を新たな「埃の位置」とします。その上で「埃の位置」をグラフ化すれば、１つの埃が風に舞って移動する様子がシミュレーションできます。
　実際に関数式を組もうとすると、一番苦労するのは②の「部屋の隅から埃までの距離」でしょうか。壁が２か所あるので、そのうちの「近い方」までの距離を表す式を立てたいわけですが、さてどうしましょうか。
　期待通りの動きをするまであれこれ試行錯誤していただきたいところですが、方法は３つくらいあります。

　　○　= IF (埃の位置>0 , 1-埃の位置 , 1+埃の位置)
　　○　= MIN (1-埃の位置 , 1+埃の位置)
　　○　= 1-ABS (埃の位置)

　以上のことをエクセル・シートに入力してみましょう。セル B3 , C3 , D3 , E3 に関数式を入力し、下方向にコピーして、E 列をグラフ化すれば、１つの埃が風に舞って移動する様子がシミュレーションできます。「数式リボン」の「シート再計算ボタン」を押せば何度でもシミュレーションできます。

　　　◇ セル B3 の式は　= RAND ( )－0.5
　　　◇ セル C3 の式は　= IF(E2>0 , 1－E2 , 1＋E2)
　　　　　　　または　　 = MIN (1＋E2 , 1－E2)
　　　　　　 もしくは　　= 1－ABS(E2)
　　　◇ セル D3 の式は　= B3＊C3
　　　◇ セル E3 の式は　= E2＋D3

　３回シミュレーションしたところ、次のようなグラフが描けました。横軸が「時間」、縦軸が「埃の位置」です。

　埃がふわふわと部屋の隅に移動していく様子が見て取れますね。

埃は部屋の隅にたまる

　「１つの埃」でうまく出来たら、次は「たくさんの埃で」やってみよう。上で作った４つの関数式は１つの関数式で書くことができる。そうすると、１列で１つの埃の動きを再現できることになり、その列を右方向にコピーすればたくさんの埃を扱うことができる。このようにして「埃が部屋の隅にたまる」様子をエクセルでビジュアルにシミュレーションしてみよう。

　上で４つのセルに入力した関数式、

　　　セル B3 ：　= RAND ( )－0.5
　　　セル C3 ：　= 1－ABS(E2)
　　　セル D3 ：　= B3＊C3
　　　セル E3 ：　= E2＋D3

は次のような１つの関数式で書けます。

　　　セル B3 ：　＝ B2＋(RAND( )－0.5)＊(1－ABS(B2))

　これを下方向にコピーすれば、１列で１つの埃の動きをシミュレーションできます。その上でさらに列ごと右にコピーすれば、たくさんの埃の動きをシミュレーションできます。
　25 個の埃の位置を 50 単位時間まで動かしたのが、次のシートです。右下のグラフはセル B52～Z52 を選択して「散布図」グラフを選んだものです。部屋の隅の方に埃が多く集まり、中ほどには少ない様子が見て取れますね。

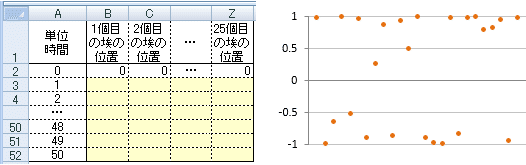
　ところで、散布図は高校数学1の「データ分析」の項目で相関係数とともに出てくるグラフですから、高校生にとっては馴染みのあるグラフです。その散布図がここではビジュアルに効果的に使えていますね。
　埃１つの方もたくさんの埃の方も「シート再計算ボタン」を押せば何度でもシミュレーションできます。ふわふわ、ふらふら、こんもり、ぱらぱら、楽しいですよ。
　なお、この埃の実習はこれだけでも十分楽しいですからぜひやっていただきたいのですが、関数式に「条件付き確率」の式を組み込むと、ベイズ推定をシミュレーションできます。意外と使い回しが効くんですよ。

シミュレーション・ソフトとしてのエクセルの利用

　記事「プログラミング的思考とは？」に私は書きました。

○　思いついたこと・考えたこと・イメージしたことをデジタルの世界で実現すること、それがプログラミング。
○　目線が遠く（ゴール）と近く（コード）と全体（システム）とを自由に行き来すること、それがプログラミング的思考。
○　その一連の作業のあらゆる場面で「言葉にする」ことがとても大事。

　これらのことを「埃」の問題を例に見てみましょう。

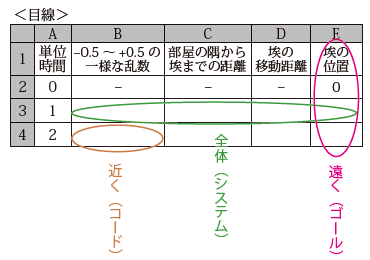
　遠くを見つめる望遠鏡目線と、近くを凝視する顕微鏡目線と、全体を見渡す鳥の目線の３つが連動して、少しずつモデルが出来ていきます。

　モデルが見えてきたら、ステップごとに標題をつけます。これは「自分がいま何をやろうとしているのか」を意識化することでもあります。同時並行で関数式を立てますが、その際はエクセル君にわかる言葉でやさしく語りかけなければいけません。そして最後にグラフ化することで、うまくできているかどうかを確認できます。また、うまくいった暁にはみんなで共有できるものになります。
　実際の作業は行きつ戻りつになるでしょう。失敗しながら修正していくうちに、だんだんとモデルがくっきりしてくるでしょう。そして期待通りのグラフが描けたら完成です。
　記事「プログラミング的思考とは？」に私は「統計＋数学＋プログラミング＝人工知能」と書きました。そのうち統計処理をするにはエクセルが最適でしょう。エクセルの関数式を立てる際に一般化したり論理構造を考えたりすることで、数学的な考え方が身につきます。そしてたった今見たように、エクセルを使うことでプログラミング的思考も身につきます。
　エクセルは表計算ソフトというより、統計ソフトであり、シミュレーション・ソフトであり、プログラミング・ソフトです。そして私は思うのです。人工知能を学ぶには「エクセル→統計→人工知能」の順番で進めるのが最も効果的で効率的だろうと。数学やプログラミングから入ると、人工知能に行き着くのはだいぶ先なりそうです。
　ところで、私は授業ではマクロ（VBA＝ Visual Basic for Applications）は使わない派です。エクセル関数のうち基本的なものだけを使って、それをどう組み合わせるかを考える方が、簡単な割に多くのことを学べるからです。生徒にとって取っ付きやすくて、達成感があって、つまり楽しいからです。

◇　　　　　　◇　　　　　　◇

〜 エクセルでシミュレーションする 〜
▷ 埃が風に舞う　　　　　　　　　　
▷ 情報伝達をグラフに＝見える化する
▷ そのコイン、まとも？ いかさま？