結論を言わない証明問題（解答編）

　記事「結論を言わない証明問題」で出した５題の《解答・解説編》です。元の問題は こちら をどうぞ。

合同な三角形を探せ

【１】下図において △ABC と △CDE はどちらも正三角形である。
　　　このとき、△＿＿＿ ≡ △＿＿＿ が成り立つ。

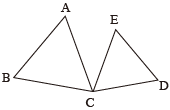
※　まず空欄を埋めて、そして証明してみよう。

《解説・解答》
　補助線を引いて、合同な三角形を探してみよう。つなげるのは A と D、A と E、B と D、B と E の４本だが、このうち A と D、B と E の２本を引くと、△ACD と △BCE が合同になっているように見えないか？

　　　　　（証明）
△ACD と △BCE において、
　　AC＝BC　（△ABC は正三角形）
　　CD＝CE　（△CDE は正三角形）
　∠ACD＝∠BCE　（＝60°＋∠ACE）
よって、２辺とその間の角が等しいから、
　△ACD ≡ △BCE //

　本当は結論を与えないだけではなくて、設問に図を描かずに、図を描くことも解答者に求めようかと思ったのだが、そうすると「場合分け」をしなければならないことになって難易度が俄然高くなりそうなので、図は与えることにした。

同一円周上にある４点を探せ

【２】下図で２円は点 P で接し、PQ は２円の接線である。
　　　このとき、４点 ＿＿＿＿＿＿＿＿ は同一円周上にある。

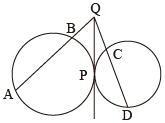
※　まず空欄を埋めて、そして証明してみよう。

《解説・解答》
　一見「４点 B , P , C , Q が同一円周上にある？」ようにも見えるが、残念ながらこれは違う。
「４点 A , B , C , D が同一円周上にあるか？」というと…
　これ以外には他に同一円周上にあるような４点はなさそうだから、
「４点 A , B , C , D が同一円周上にある」と「仮説」を立てよう。
　次に「検証」。うまく検証できれば、すなわち証明したことになる。

（証明）
PQ は左円の接線だから、方べきの定理より PQ^2＝PA・PB … ①
PQ は右円の接線でもあるから、方べきの定理より PQ^2＝PC・PD … ②
① , ②より　PA・PB＝PC・PD
方べきの定理の逆より「４点 A , B , C , D は同一円周上にある」。//

合同か？

【３】円に内接する四角形 ABCD がある。
　　　対角線 AC と BD の交点を E とする。
　　　AC=BD のとき、△ABE≡△DCE は成り立つか？

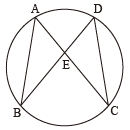
※　「成り立つ」と言うなら、証明してね。
　　「成り立たない」と言うなら、反例を挙げて。

∠ABE＝∠DCE（弧ADの円周角）
∠BAE＝∠CDE（弧BCの円周角）
∠AEB＝∠DEC（対頂角）
から　相似 △ABE∽△DCE（２角相等）はすぐ言える。

　けれども、そこからが難しい。
　対応する辺（AB と DC、AE と DE、BE と CE）のいずれかが１つでも等しいと言えれば 合同 △ABE≡△DCE（１辺両端角相等）とわかるのだが、さて、どうしようか。

　ところで、本当に「△ABE≡△DCE」なのだろうか。反例はあるのだろうか。
　何はともあれ、証明を目指してみよう。

　　　　＜証明１＞
AC＝DB より AE＝DE , BE＝CE　　←　本当に言えるのか？
また ∠AEC＝∠DEC（対頂角）
２辺とその間の角が等しいから △ABE≡△DCE

　　　　＜証明２＞
∠BAC＝∠BDC より 四角形ABCDは円に内接する。
AC＝DB より ∠ABC＝∠DCB　　←　等しい長さの弦に対する円周角？
BC は共通だから １辺両端角相等により △ABC≡△DCB
よって AB＝DC　１辺両端角相等により △ABE≡△DCE

　　　　＜証明３＞
AC と DB の交点を F とする。　　←　そもそも交わるのか？
∠FAC＝∠FDB（∠BAC＝∠BDC の補角）
∠ACF＝∠DBF（△ABEと△DCE において他の２角が等しいから）
１辺とその両端の角が等しいから △FDB≡△FAC
よって FB＝FC , FD＝FA　よって AB＝DC
１辺とその両端の角が等しいから △ABE≡△DCE

再び相似に戻って「方べきの定理」を使ってみると、

AC＝DB＝1 としても一般性を失わないから
AE＝a , DE＝b とおいて CE＝1−a , BE＝1−b だから
　　a(1−a)＝b(1−b)（方べきの定理）
　　　⇔　a−a^2＝b−b^2
　　　⇔　a−b−a^2＋b^2＝0
　　　⇔　(a−b)−(a＋b)(a−b)＝0
　　　⇔　(a−b)(1−a−b)＝0
　　　⇔　a＝b　または　a＋b＝1

（ⅰ）a＝b のときは「△ABE≡△DCE」が成り立つ。

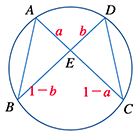
　　　　けれども
（ⅱ）a＋b＝1 のとき、
　　　CE＝1−a＝b , BE＝1−b＝a となって、
　　　この場合は「△ABE≡△DCE」は成り立たない。
　　　これが「反例」である。

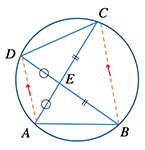
すなわち「AC=BD のとき、△ABE≡△DCE」は成り立たない。

つまり、こういうことだ。
「円に内接し、かつ対角線の長さが等しい四角形」は「等脚台形」になる。
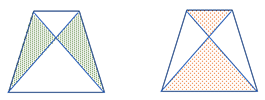
等脚台形を２本の対角線で切ってできる４つの三角形のうち、下左図の２つの三角形は合同である。一方、下右図の２つの三角形は相似な二等辺三角形ではあるが、合同ではない。（これが反例にあたる）

角の２等分線を３本引くと．．．

【４】 二等辺三角形でない△ABC がある。
　　　∠A の内角の二等分線と直線 BC の交点を D 、
　　　∠B の内角の二等分線と直線 CA の交点を E 、
　　　∠C の内角の二等分線と直線 AB の交点を F とする。
　　　このとき ______________________________ 。

　これは結果を知っている人も多いでしょう。中学・数学の教科書にも証明つきで載っています。三角形の「内心」ですね。
　 いろんな証明ができますが、ここでは「角の２等分線公式」と「チェバの定理の逆」を使った証明を載せておきます。

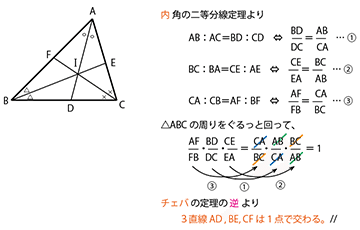
　では、次の問題はどうでしょうか？

【４’】 二等辺三角形でない△ABC がある。
　　　∠A の外角の二等分線と直線 BC の交点を D 、
　　　∠B の外角の二等分線と直線 CA の交点を E 、
　　　∠C の外角の二等分線と直線 AB の交点を F とする。
　　　このとき ______________________________ 。

　【４】の「内角」を「外角」に変えただけなのですが、この場合に「必ず成り立つ」ことをまず探してください。そしてその上で、それを証明してください。
　まず図を描きましょう。丁寧に、ある程度正確に描いてくださいね。雑に描いたら、たぶん何も見えてこないでしょう。

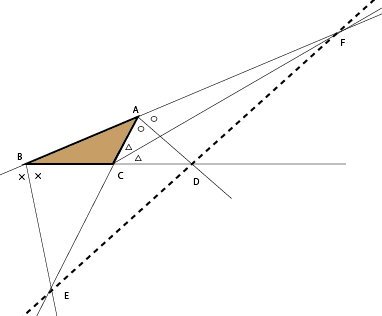
　きれいに描けば「３点 D , E , F が一直線上に並んでいる」ことが見えるでしょう。
　では、続いて、本当にそうなのかどうかを証明してみましょう。

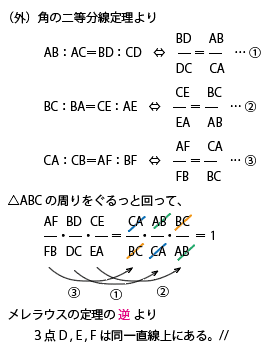
　ここでもう一度【４】の証明と【４’】の証明を見比べてください。よく似ていますよ。いや、似ているどころか、ほぼ同じだと行って良いくらいです。
　証明のスタート部分で【４】の「内角」と【４’】の「外角」が違っていて、そこから先は全く同じ文・式が続きます。そして最後から２行目で「チェバ」と「メネラウス」の部分が違って、最終結論【４】の「３直線が１点で交わる」と【４’】の「３点が一直線上にある」が全く違う。両者を比較すると、平面幾何の理解が深まります。

四角形の頂点からの距離の和が最大になる点

【５】四角形ABCDにおいて、頂点 A , B , C , D からの距離の和
　　　PA+PB+PC+PD が最小になるような点 P はどこにあるか？

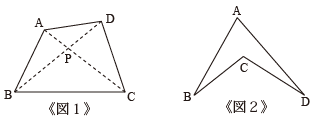
　《図１》のような四角形なら、直感的に「対角線の交点じゃないか」と見当がつくだろう。証明してみよう。

《証明》
《図１》の四角形 ABCD において、対角線 AC と BD の交点を P とする。
線分 AC 上の P 以外の点を P' とすると、
　　　　PA+PC＝P'A+P'C　,　PB+PD＜P'B+P'D
　 　　　　　　より PA+PB+PC+PD＜P'A+P'B+P'C+P'D
線分 BD 上の P 以外の点を P'' とすると、
　　　　PA+PC＜P'A+P'C　,　PB+PD＝P''B+P''D
　 　　　　　　より PA+PB+PC+PD＜P''A+P''B+P''C+P''D
それ以外の点、もちろん P 以外の点を P''' とすると、
　　　　PA+PC＜P'''A+P'''C　,　PB+PD＜P'''B+P'''D
　 　　　　　　より PA+PB+PC+PD＜P'''A+P'''B+P'''C+P'''D
すなわち４頂点から P 以外の点までの距離の和は、４頂点から点 P までの距離の和より大きい。
よって、PA+PB+PC+PD が最小になるような点 P は対角線の交点である。//

　《図２》の四角形については・・・私にはよく分かりません。助けてください。

◇　　　　　　◇　　　　　　◇

〜 私の数学教育論 〜
▷ 結論を言わない証明問題　＋　解答編
▷ 数学屋が売れる時代になってきた　　
▷ 「３」のマジック