いっきに三角関数の微分と積分

　数学Ⅱの範囲が一通り理解できている前提で、いっきに三角関数の微分・積分までやってしまうためのプリントを作ってみた。A4用紙１枚に収まって、授業１コマ（50分）の半分でやってしまえる。授業の残り半分で「いっきに指数・対数の微分と積分」をやって、授業１コマで数学Ⅲの全貌をざっくり見てしまおうという試みだ。
　ところで、以下の話には、教科書の説明と異なっている部分や、直感に頼って厳密さを欠いている部分がある。つまりザツ、念のため。

◯　$${y=\sin x}$$ 上の各点での傾きをとってみると、
　　　$${x=90 ^{\circ}  ,  270 ^{\circ} ,  \cdots}$$ で傾き $${0}$$ は分かるが、
　　　$${x=0 ^{\circ}  ,  180 ^{\circ} ,  \cdots}$$ の傾きは？
　縦軸と横軸の単位が違うので、どうにでもなる？

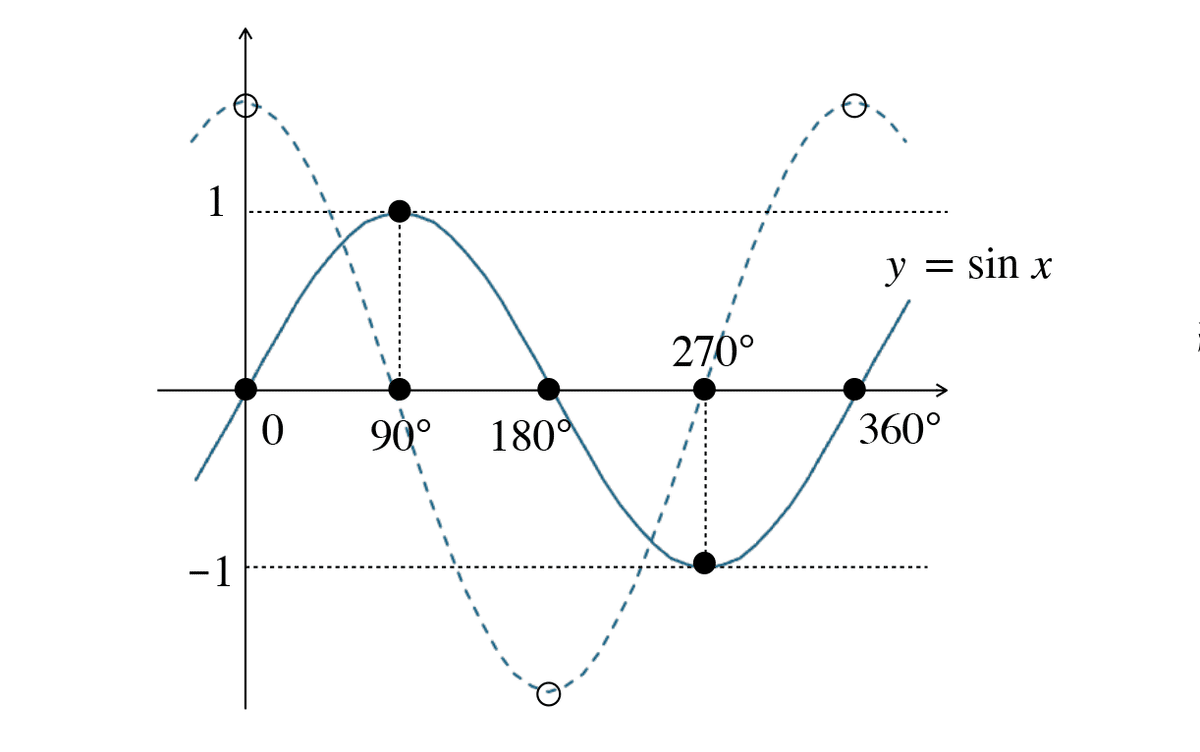
◯　$${x=0 ^{\circ}}$$ での傾きが $${1}$$ になってくれたら嬉しいね。
　　　もしかして　　ラジアン？
　　　もしかして　　$${\left( \sin x \right)'=\cos x}$$？
　そもそもラジアンってなんだっけ？

（縦軸・横軸の比率を π＝3.14 でほぼ正しく描いた）

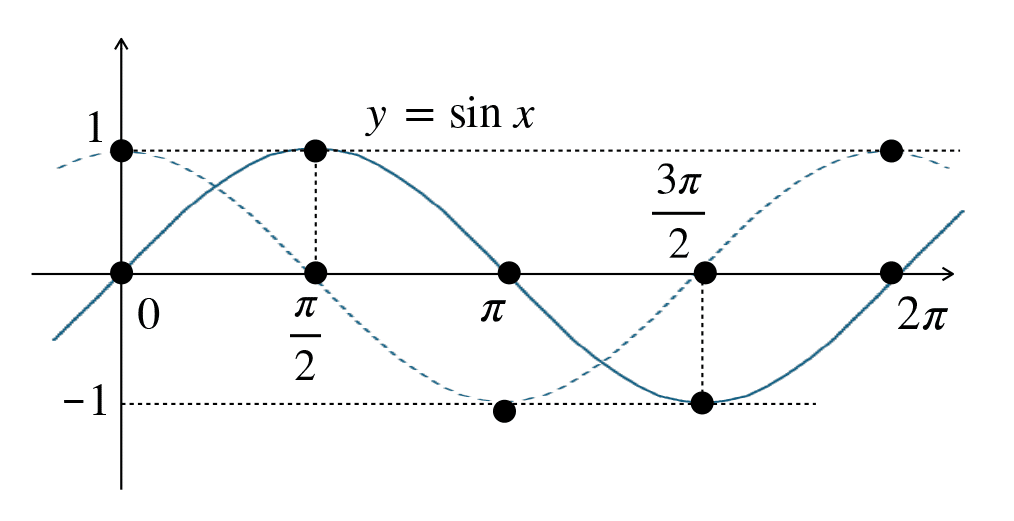
◯　もし $${\left( \sin x \right)'=\cos x}$$ が成り立つ なら、
　　$${\left( \cos x \right)'=\left( \sin \left(x+\dfrac{\pi}{2}\right) \right)'=\cos \left(x+\dfrac{\pi}{2}\right)=-\sin x}$$
　　$${\left( \sin x \right)'=\cos x}$$ より $${\int \cos x dx = \sin x+\mathrm{C}}$$
　　$${\left( \cos x \right)'=-\sin x}$$ より $${\int \sin x dx = -\cos x+\mathrm{C}}$$

◯　もし $${\left( \sin x \right)'=\cos x}$$ が成り立つ なら、
　　$${f(x)= \sin x}$$ のとき $${f'(x)=\cos x}$$ より $${f'(0)=\cos 0=1}$$
　　　　　　　　　$${\int_{0}^{\frac{\pi}{2}} f(x) dx= \int_{0}^{\frac{\pi}{2}} \sin x dx=\Bigl[-\cos x \Bigl]_{0}^{\frac{\pi}{2}}}$$
　　　　　　　　　　　　　$${= - \cos \dfrac{\pi}{2} + \cos 0= 0+1=1}$$

◯　さて、$${\left( \sin x \right)'=\cos x}$$ は成り立つのか？
　　$${\left( \sin x \right)'=\lim_{h\to 0} \dfrac{\sin (x+h) -\sin x}{h}}$$
　　　　　$${=\lim_{h\to 0} \dfrac{\sin x \cos h + \cos x \sin h -\sin x}{h}}$$
　　　　　$${=\lim_{h \to 0} \left( \dfrac{\sin h} {h} \cos x - \dfrac{1-\cos h} {h}\sin x \right)}$$ … ①

ここで $${\dfrac{\sin h} {h} }$$ と $${ \dfrac{1-\cos h} {h}}$$ について考える。
　$${h \to 0}$$ のとき、分母$${ \to 0}$$ , 分子$${ \to 0}$$ となるが、$${ \dfrac{\to 0} {\to 0}}$$ がどうなるかはマチマチ、モノに依る。エクセルでやってみると、

$${\lim_{h \to 0} \dfrac{\sin h} {h} =1}$$ と $${\lim_{h \to 0} \dfrac{1-\cos h} {h}=0}$$ となりそうだ。
　それを採用すると、① $${=\cos x}$$ となる。つまり$${\left( \sin x \right)'=\cos x}$$ が成り立つ。めでたしめでたし。