「鳩の巣原理」で考えてみよう

【問】１辺の長さが 2 の正三角形の周上または内部にいくつかの点を置く。
　　　ただし、どの２点間の距離も 1より大きく なるようにする。
　　　最大で点をいくつ置けるか？

　ところで、答えを「n 個」と言うためには、

・ n 個でうまくいく例を示す
・ n＋1 個では不可能なことを示す

必要があります。
　なお、上の文にあるように、２点間の距離を「１より大きく」してくださいね。「ちょうど１はダメ」ですよ。
　ここで「鳩の巣原理」という考えを紹介しましょう。これは別名「部屋割り論法」とも言われます。

・ n 個の巣に n＋1 羽の鳩が入る場合、どれかの巣には２羽以上の鳩が入る
・ n 個の部屋に n＋1 人が入る場合、どれかの部屋には２人以上の人が入る

という原理です。いかにも当たり前のことを言っているわけですが、上の【問】に答えるには、その考え方が効果的に使えます。と言うより、それを使わずに答えるのは困難です。

　では、考えてみましょう。まず、４点は置けます。たとえば（図１）のように、正三角形の頂点に３つ、４つ目を正三角形の重心の位置に置けば、条件を満たします。このとき２点間の距離は 2 か 2／√3 ですから「どの２点間の距離も１より大きい」ですね。
　けれども、５点を置こうとすると、なかなか置けないでしょう。点をどう動かしても、どれか２点の距離が１以下になってしまうでしょう。というわけで、答えは「４点」となりそうです。
　では、どうすれば「５点は置けない」ことをきちんと示せるでしょうか。はい、ここで登場するのが「鳩の巣原理」です。元の「１辺の長さが２の正三角形」を（図２）のように「１辺の長さが１の４つの正三角形」に分けて考えましょう。５つの点を置くと、必ずどこかの小三角形の周上または内部に２点置くことになります。その２点の距離は必ず１以下になりますから、「５点は置けない」と分かるのです。

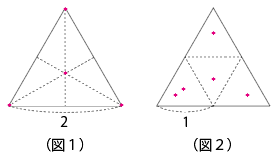
　この考え方が「鳩の巣原理」です。４つに分けた小さい三角形が「巣」にあたります。５つの点が「鳩」です。２点間の距離を１より大きくするには、点（鳩）を別々の小三角形（別々の巣）の中に入れなければならないのですが、５点（５羽の鳩）を別々の４つの小三角形（４つの巣）の中に入れるのは無理ですね。
　当たり前すぎて、わざわざ名前をつけるほどのことでもないように思える「鳩の巣原理」。でも、この問題で「５点は置けない」ことを示すのに、他にやり方が見つからないのです。地味だけど、すごい威力とでも言いましょうか。

◇　　　　　　◇　　　　　　◇

〜 考えるための数学問題集 〜
▷ わかれば瞬殺、答えを見れば一目瞭然
▷ ピタゴラス数は３,４,５の倍数から成る
▷ 相似な図形　　　　　　　　　　　　
▷ 「鳩の巣原理」で考えてみよう　　　
▷ 結論を言わない証明問題