円柱どうし、角柱どうしの交わり

◇　円柱２つを垂直に（中心線が交わるように）ぶつけると、重なった部分はどんな図形になるか？
◇　角柱２つ（下図のように置く）を垂直にぶつけると、重なった部分はどんな図形になるか？
◇　円柱３つを垂直にぶつけたら？　角柱３つを垂直にぶつけたら？　見取り図は？　体積は？

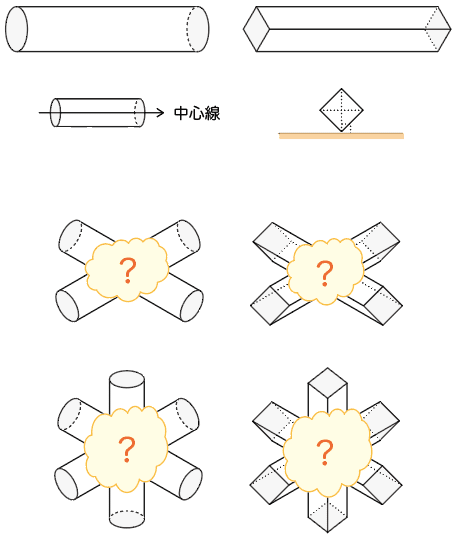
角柱２本の交わり

　断面が正方形である角柱が２つあって、床面に対して下図のように置いてあります。

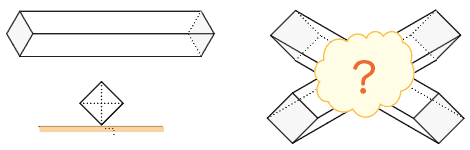
　２つの角柱が垂直に交わっているとき、重なっている部分はどんな立体でしょうか？　あわせて、その立体の体積を、正方形の対角線の長さを 1 として求めてください。

　見取り図を描いてみましょう。まず投影図を、続いて俯瞰図を描くのがいいでしょう。

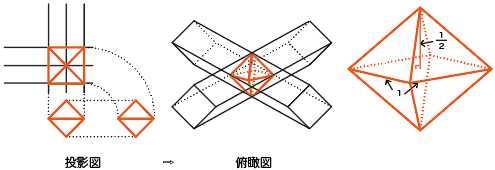
　この立体は 八面体 ですが、正八面体とは微妙に違って、正八面体を高さ方向に少し縮めた形になります。
　また、この立体が四角すいを２つ重ねたものであることを利用して、体積は 1/ 3 です。

円柱２本の交わり

　円柱が２つあって、中心線が垂直に交わっています。

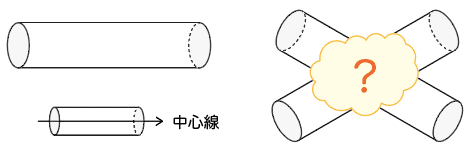
　２つの円柱が重なっている部分はどんな立体でしょうか？　あわせて、その立体の体積を、底面の円の半径を 1 として求めてください。

　見取り図を描いてみましょう。まず投影図を、続いてキャビネット図を描くのがいいでしょう。
　この立体を横から見ると ○ ですが、上から見ると、□ の中に × が見えます。そのことを考えてキャビネット図を描くと、下中図のようになります。

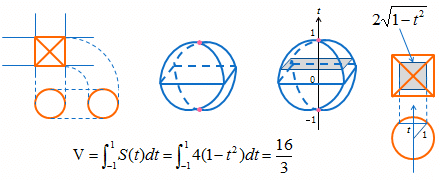
　次に、体積を求めてみましょう。高校数学でやった積分を使えば求められます。
　鉛直方向に軸をとって、軸に垂直な平面でこの立体を切ると、切り口は正方形になります。正方形の一辺の長さを求め、２乗して断面積を出し、それを −1 から 1 まで積分すれば完成です。体積は 16/3 です。

円柱３本の交わり

　円柱２本（の中心線）が垂直に交わるときの交わり部分について考えたところで、さらにもう１つ円柱を加えて「円柱３本が垂直に交わるときの交わり」について考えましょう。
　どんな形？　体積は？

　円柱２本の交わりはこの（↓）ようなものでした。

　これをもう１つの円柱で切ると、上と下はそのままで、中ほどの回りの部分が（↑）削り取られます。
　ここで、削られずに上に残った部分を Ａ と呼ぶことにします。Ａ の体積は、円柱２本の交わりを求めたときと同じやり方で積分で求められます。
　また対照性を考えると、円柱３つの交わりの図形は、立方体の６面に Ａ がくっついたものになります。
　というわけで、その体積は上の計算を実行して、 8 (2-√2)　となります。

角柱３本の交わり

　「角柱２本の交わり → 円柱２本の交わり → 円柱３本の交わり」と、ここまでやってきました。あと１つ、行ってみましょう。

　「角柱３本が垂直に交わるときの交わり」はどんな形？　体積は？

　角柱２本の交わりは八面体で、底面の対角線の長さが 1 のときの体積は 1/3 でした。

　ここに３本目の角柱を突き通すと、八面体の辺の中点を通って、４ヶ所を切り落とすことになります。
　切り落とす１ヶ所の体積は、相似比を考えて、八面体の 1/16 ですから、
残った部分の体積は 1/3×(1－4/16)＝ 1/4 です。これが、角柱３本の交わりの体積です。

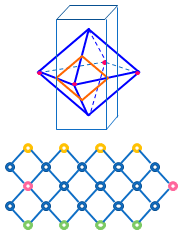
　ところでこの立体は、右のような骨組みの同じ色の点をつないでできる
立体と同じです。 右図の辺はどれも同じ長さですが、これを立体として組み立てると、上下の８つの四角形が縦に伸びて、中ほどの４つの四角形が横に伸びて、すべてが合同なひし形になります。
　これを 「ひし形１２面体」 と呼びます。 正多面体ではありませんが。

◇　　　　　　◇　　　　　　◇

〜 立体図形の描き方 〜　
▷ 見取り図３種　　　　　　　　　
▷ 正多面体つながり　　　　　　　
▷ 描く空間図形　　　　　　　　　
▷ 立方体と正四面体の展開図　　　
▷ 円柱どうし、角柱どうしの交わり