
宇宙のサイズは465億光年?
JWST(ジェイムズ・ウェッブ宇宙望遠鏡)は宇宙で最初にできた星、First Star を見つけ出そうとして、観測を続けている。
表題の画像は、そんなJWSTが撮影したものである。この中に映っているモスラ(Mothra)と名付けられた銀河は、ビッグバンから30億年後、つまり100億年以上前の銀河だと言う。
このように撮影された銀河は、100億年以上前に放たれた光を見ていることになる。その銀河は現在、どこに存在しているのだろう? 100億年先?
いやいや、宇宙は膨張を続けているのだから、100億年もたったら、もっとはるか遠くに離れているのではないか?
それなら光を出した100億年前には、どこにいたのだろう?
そんな疑問を解消すべく、いろいろと調べてみた。
赤方偏移と距離
そもそも天体までの距離はどうやって測るのだろう。
近くの天体なら、三角測量で距離を測ることができるが、ちょっと遠くなると難しくなる。そこで、絶対的な明るさが推定できる「セファイド変光星」という星を使う。この方法で近くの銀河までの距離がわかる。
さらに遠い銀河の場合には、絶対的な明るさが決まっているIa型という
超新星を使う。
さらに遠くなると、星が遠ざかっている速度から推定する。
遠くの星からの光は、スペクトルが赤い方向に偏移している(赤方偏移)。これをドップラー効果によるものと考えると、遠くの星は地球から遠ざかっていることになる。そしてその遠ざかる速度は、遠いほど速くなる。
遠ざかる速度=ハッブル数✕星までの距離
そして遠ざかる速度が速いほど、赤方偏移は大きくなる。そこで赤方偏移を測定し、それから星までの距離を推定するわけである。
赤方偏移zは以下のように定義される。
$${ z=\dfrac{\lambda}{\lambda_0} -1}$$
ここで$${\lambda}$$は観測された波長であり、$${\lambda_0}$$は元の波長である。
赤方偏移は、遠くの星が遠ざかっていることによるドップラー効果として説明されることが多いが、宇宙が膨張しているために光が引き伸ばされたと考えることもできる。

冒頭に述べたMothraという銀河の赤方偏移zはおよそ2.2であることから、ビッグバンから30億年後と推定されている。
Mothraが光を放ってから現在までの間に、宇宙は3.2倍(1+z=3.2)に膨張したと言うことになる。
宇宙膨張の理論
赤方偏移から距離を求めるためには、宇宙がどのように広がっていったかを知る必要があり、それはアインシュタインの一般相対性理論で計算することができる。
とはいっても様々な前提条件が必要であり、前提条件によって結果は大きく異なる。ここでは日本天文学会の天文学辞典に掲載されているモデルを元に説明する。
前提とするパラメータを以下のように仮定する。
ハッブル数 $${H_0 = 67.66km s^{-1} {Mpc}^{-1}}$$
密度パラメータ $${\Omega_{m0} = 0.3111}$$
宇宙定数 $${\Omega_{\Lambda0} = 0.6889}$$
このパラメータから、経過時間tと、宇宙の大きさxは次の計算式で求めることができる(らしい)。
$${t(z) = \dfrac{1}{H_0} \displaystyle \int_{0}^{z} \dfrac{dz}{(1+z)\sqrt{(1+z)^3 \Omega_{m0}+\Omega_{\Lambda0}}}}$$
$${x(z) = \dfrac{c}{H_0} \displaystyle \int_{0}^{z} \dfrac{dz}{\sqrt{(1+z)^3 \Omega_{m0}+\Omega_{\Lambda0}}}}$$
$${x_0(z) = \dfrac{x(z)}{1+z}}$$
このような積分はとても解けないので、エクセルで数値計算した結果を下図に示す。
このようにして求めたxと時間tの関係を示したのが下図である。これは時間とともに宇宙が拡大していった様子を示している。

横軸は宇宙の大きさxであり、縦軸がビッグバンからの時間tになっている。
例えばz=1.7の赤方偏移をした銀河を見つけた場合、その銀河が100億年前、t=38億年に放った光を観測していることになる。光を放った時点での距離x0は58.4億光年で、その光が届く100億年の間に宇宙は2.7倍に膨張し、現在の距離xは158億光年と推定される。
宇宙が膨張しているので、光が出た時点で58.4億光年先にあったところまで到達するのに、100億年かかったということである。
そして100億年前の光を観測したので、その銀河は100億光年先にあるように見えるのである。
つまり、銀河までの距離には3種類があることになる。
見かけの距離 $${x_t = ct}$$ cは光の速度
当初距離 $${x_0}$$ 光が出た時点での距離
現在距離 $${x}$$ 現在の距離
これを混同しないように注意する必要がある。
宇宙背景放射
観測できる最も古い光、あるいは最も遠い光は、宇宙背景放射である。

この光(マイクロ波)の赤方偏移zは1090であり、ビッグバンの38万年後に出た光だと考えられている。この時点での宇宙の温度は3000K、出た光の波長は1μm前後であった。これが宇宙膨張で1000倍以上に引き伸ばされ、現在1mm前後のマイクロ波として観測されている。
この赤方偏移から推定できる距離は以下のようになる。
見かけの距離 $${x_t}$$:138億光年
当初距離 $${x_0}$$:4150万光年
現在距離 $${x}$$:453億光年
138億年前、4150万光年という「ご近所」から離れたところから出た光が、138億年かかって、今、届いている。そして現在は、宇宙の膨張によって453億光年の彼方に行っている。
宇宙の大きさは465億光年?

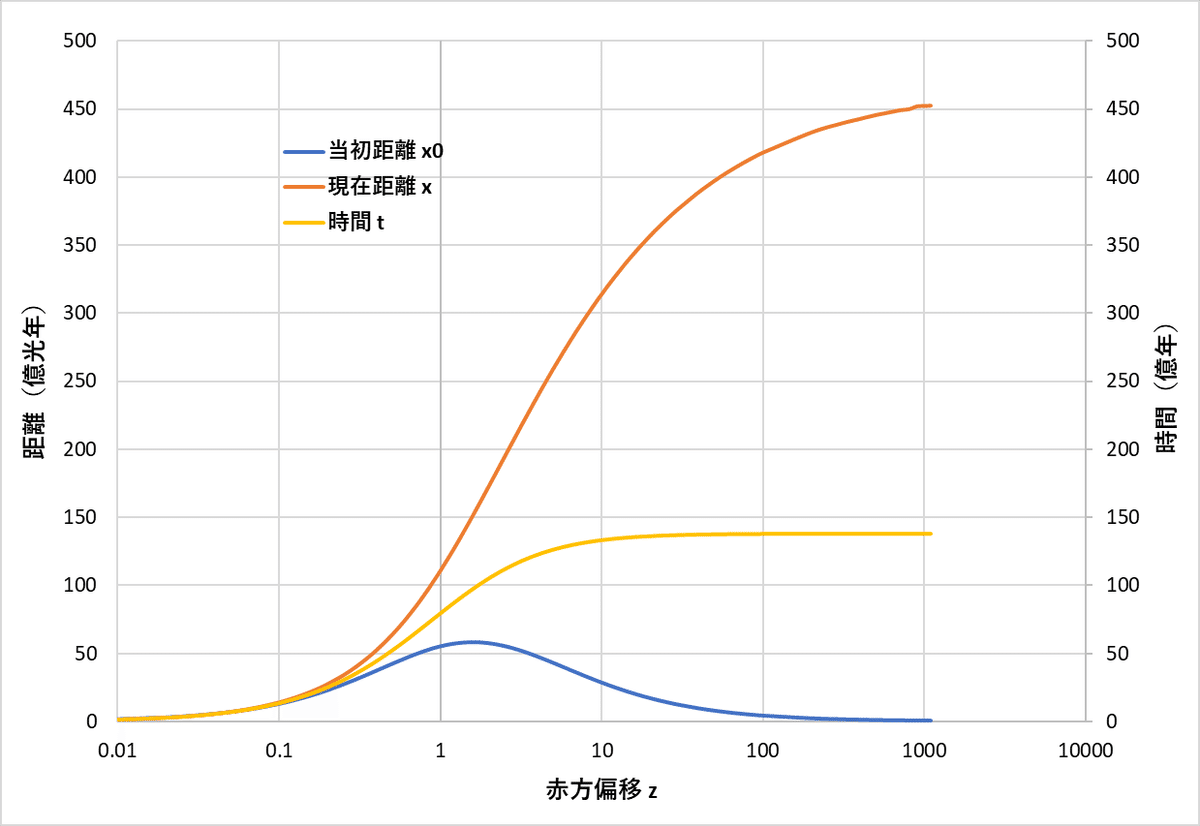
光の到達時間に対応する3つの距離を上の図に示す。これは図2の軸を変えて書き直したものである。
近くの天体では、3つの距離はほとんど同じであるが、遠くなるにつれて差が開いていく。当初距離は100億年を超えたあたりから小さくなり始め、138億年あたりでゼロになる。一方、現在距離は138億年に近づくにつれて急激に大きくなって行く。
宇宙背景放射の場合、138億光年離れたところに見えるが、光が出たときはそれよりずっと近い4150万光年のところにあり、それが今は453億光年の彼方ということであった。
そのもっと前は、宇宙がプラズマ状態であって光が進めなかったため、光や電波で観測することはできない。しかし技術が進めば、重力波なら観測できるかもしれない。
そのように理論的にはビッグバン時点の痕跡は観測可能である。その時点での距離(当初距離)はゼロであり、見かけ上の距離はおよそ138億光年、そして現在距離は465億光年と推定される。
観測可能な宇宙は半径465億光年というのは、このようにして求められたものである。
でも実際に465億光年先の何かを観測できるわけではない。観測できたとしても、それはビッグバン直後、138億年前の、すぐそばにあった場所の何かであり、現在の465億光年先の何かではない。
観測とは何?
この話、考えれば考えるほどわからなくなる。遠くを見ようとすればするほど、遠い昔の、すぐ近くだったところを拡大して見ていることになる。あたかもタイムマシン付きの顕微鏡で見ているように。
現在、宇宙が465億光年先に広がっているとしても、その光を観測することは未来永劫、不可能である。それを観測可能といって良いのだろうか。
例えば、隣に住んでいた幼馴染が毎年、遠くに引っ越していき、60年後の今、アメリカに住んでいるとしよう。その幼馴染の60年前の映像が、今届いて見ているとして、老人になりアメリカに住んでいる幼馴染を観測していることになるのだろうか?
厳密に言えば、眼の前の花を観測しているときも、花から出た光が目に到着するまでに時間がかかっている。このため現在の花を観測していることにはならない。
どこまでが許容範囲なのだろう。
観測可能な宇宙という場合、観測をどのように定義するかによって、結果は全く違ってくる。
この記事が気に入ったらサポートをしてみませんか?
