
Bilateral Series Approximationのr^-αへの収束性
定義域で連続かつ区分的に滑らかな関数φ(r),そのメリン変換
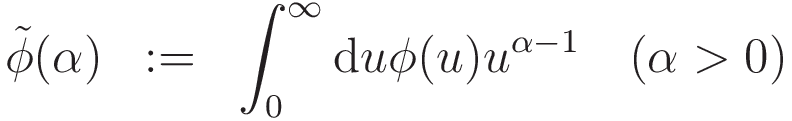
及びパラメータb( > 1)を用いて,r^-αをbilateral series expansionで近似(bilateral series approximation,以下BSA)することを考えます。

このとき,

が成立すること以下で示します。
また,φ(r)がガウス関数であったときの収束性を調べます。
ポアソン和公式
BSAはjに関する和になっていますが,ポアソン和公式を用いてjを連続変数xで表す形に変形します。

変数変換
次に以下の変数変換を考えます。
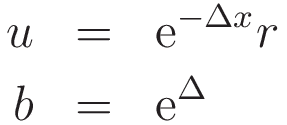
このとき,

となります。
また,「x: -∞ → ∞」に対して「u: ∞ → 0」となるため,BSAの表式は

と変形することができます。
更に式変形すると

となります。
以上より,目的の表式を得ることができました。
根の存在
上式では誤差の上限が与えられますが,特定のrに対しては0を取る(=根が存在する)性質もあります。
以下では,

を用いることにより,1 ≦ r < bの範囲に最低1つ以上の根があることを示します。
具体的に計算していくと,

となります。
r^-1は1 ≦ r < bの範囲で常に正の値をとるため,積分が0になるためには
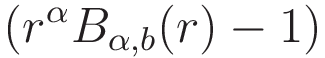
が1 ≦ r < bの範囲で最低でも1回は正→負もしくは負→正と符合が反転する必要があります。
これは
![]()
を満たすr_0が最低1つは存在することと等価です。
φ(r)がガウス関数の場合
φ(r)がガウス関数の場合,そのメリン変換はガンマ関数になります。

このとき,BSAのr^-αに対する誤差の不等式は

となります。
右辺のn=1の項

に着目してみます。
Δ≂0(b≂1)の場合,ガンマ関数をスターリングの公式を用いて近似することができます。

上式の右辺を整理すると,

となります。これより,

となります。

より,

これより,n=1の項は1/Δに対して指数関数的に減衰することが分かります。|n| > 1は更に早く減衰することを考慮すると,不等式の右辺は|n| = 1以外の項の寄与が小さいため,

が大よそ成立することが期待されます。
Δ→0で右辺が0に収束するため,BSAはr^αに収束します。
参考文献
1. J. Chem. Phys. 152, 084113 (2020)
この記事が気に入ったらサポートをしてみませんか?
