PRML自習ノート - chapter 8 -

2022年7月30日 22:16

Exercise (8.1) - (8.10)

Exercise (8.1)

$$
\begin{align*}
\int{\rm d}\mathbf{x}p(\mathbf{x})&=\prod_{k=1}^K\int{\rm d}x_kp(x_k|pa_k)\\
&=\prod_{k=1}^K1\\
&=1
\end{align*}
$$

Exercise (8.2)

例えば，$${i,j,k\ (i < j< k)}$$とナンバリングされたノードがあるとき，closed cycleを形成するためには，$${j\rightarrow i}$$や$${k\rightarrow i}$$といったように番号の大きい方から小さい方への矢印もないと成立しない。そのため，自分よりも大きい番号を持つノードにしか矢印で結べない条件ではclosed cycleは存在しない。

Exercise (8.3)

$$
\begin{align*}
p(a=0)&=p(a=0,b=0,c=0)+p(a=0,b=1,c=0)+p(a=0,b=0,c=1)+p(a=0,b=1,c=1)\\
&=0.192+0.048+0.144+0.216\\
&=0.6\\
p(b=0)&=p(a=0,b=0,c=0)+p(a=1,b=0,c=0)+p(a=0,b=0,c=1)+p(a=1,b=0,c=1)\\
&=0.192+0.192+0.144+0.064\\
&=0.592\\
p(a=1)&=p(a=1,b=0,c=0)+p(a=1,b=1,c=0)+p(a=1,b=0,c=1)+p(a=1,b=1,c=1)\\
&=0.192+0.048+0.064+0.096\\
&=0.4\\
p(b=1)&=p(a=0,b=1,c=0)+p(a=1,b=1,c=0)+p(a=0,b=1,c=1)+p(a=1,b=1,c=1)\\
&=0.048+0.048+0.216+0.096\\
&=0.408\\
p(a=0,b=0)&=p(a=0,b=0,c=0)+p(a=0,b=0,c=1)\\
&=0.192+0.144\\
&=0.336\\
&\neq 0.6*0.592\\
p(a=0,b=1)&=p(a=0,b=1,c=0)+p(a=0,b=1,c=1)\\
&=0.048+0.216\\
&=0.264\\
&\neq 0.6*0.408\\
p(a=1,b=0)&=p(a=1,b=0,c=0)+p(a=1,b=0,c=1)\\
&=0.192+0.064\\
&=0.256\\
&\neq 0.4*0.592\\
p(a=1,b=1)&=p(a=1,b=1,c=0)+p(a=1,b=1,c=1)\\
&=0.048+0.096\\
&=0.144\\
&\neq 0.4*0.408\\
\therefore p(a,b)&\neq p(a)p(b)
\end{align*}
$$

$$
\begin{align*}
p(c=0)&=p(a=0,b=0,c=0)+p(a=0,b=1,c=0)+p(a=1,b=0,c=0)+p(a=1,b=1,c=0)\\
&=0.192+0.048+0.192+0.048\\
&=0.48\\
p(c=1)&=p(a=0,b=0,c=1)+p(a=0,b=1,c=1)+p(a=1,b=0,c=1)+p(a=1,b=1,c=1)\\
&=0.144+0.216+0.064+0.096\\
&=0.52\\
p(a=0,c=0)&=p(a=0,b=0,c=0)+p(a=0,b=1,c=0)\\
&=0.192+0.048\\
&=0.24\\
p(a=0,c=1)&=p(a=0,b=0,c=1)+p(a=0,b=1,c=1)\\
&=0.144+0.216\\
&=0.36\\
p(a=1,c=0)&=p(a=1,b=0,c=0)+p(a=1,b=1,c=0)\\
&=0.192+0.048\\
&=0.24\\
p(a=1,c=1)&=p(a=1,b=0,c=1)+p(a=1,b=1,c=1)\\
&=0.064+0.096\\
&=0.16\\
p(b=0,c=0)&=p(a=0,b=0,c=0)+p(a=1,b=0,c=0)\\
&=0.192+0.192\\
&=0.384\\
p(b=0,c=1)&=p(a=0,b=0,c=1)+p(a=1,b=0,c=1)\\
&=0.144+0.064\\
&=0.208\\
p(b=1,c=0)&=p(a=0,b=1,c=0)+p(a=1,b=1,c=0)\\
&=0.048+0.048\\
&=0.096\\
p(b=1,c=1)&=p(a=0,b=1,c=1)+p(a=1,b=1,c=1)\\
&=0.216+0.096\\
&=0.312\\
p(a=0,b=0|c=0)&=\frac{p(a=0,b=0,c=0)}{p(c=0)}\\
&=\frac{0.192}{0.48}\\
&=\frac{0.24}{0.48}\frac{0.384}{0.48}\\
&=p(a=0|c=0)p(b=0|c=0)\\
p(a=1,b=0|c=0)&=\frac{p(a=1,b=0,c=0)}{p(c=0)}\\
&=\frac{0.192}{0.48}\\
&=\frac{0.24}{0.48}\frac{0.384}{0.48}\\
&=p(a=1|c=0)p(b=0|c=0)\\
p(a=0,b=1|c=0)&=\frac{p(a=0,b=1,c=0)}{p(c=0)}\\
&=\frac{0.048}{0.48}\\
&=\frac{0.24}{0.48}\frac{0.096}{0.48}\\
&=p(a=0|c=0)p(b=1|c=0)\\
p(a=1,b=1|c=0)&=\frac{p(a=1,b=1,c=0)}{p(c=0)}\\
&=\frac{0.048}{0.48}\\
&=\frac{0.24}{0.48}\frac{0.096}{0.48}\\
&=p(a=1|c=0)p(b=1|c=0)\\
p(a=0,b=0|c=1)&=\frac{p(a=0,b=0,c=1)}{p(c=1)}\\
&=\frac{0.144}{0.52}\\
&=\frac{0.36}{0.52}\frac{0.208}{0.52}\\
&=p(a=0|c=1)p(b=0|c=1)\\
p(a=1,b=0|c=1)&=\frac{p(a=1,b=0,c=1)}{p(c=1)}\\
&=\frac{0.064}{0.52}\\
&=\frac{0.16}{0.52}\frac{0.208}{0.52}\\
&=p(a=1|c=1)p(b=0|c=1)\\
p(a=0,b=1|c=1)&=\frac{p(a=0,b=1,c=1)}{p(c=1)}\\
&=\frac{0.216}{0.52}\\
&=\frac{0.36}{0.52}\frac{0.312}{0.52}\\
&=p(a=0|c=1)p(b=1|c=1)\\
p(a=1,b=1|c=1)&=\frac{p(a=1,b=1,c=1)}{p(c=1)}\\
&=\frac{0.096}{0.52}\\
&=\frac{0.16}{0.52}\frac{0.312}{0.52}\\
&=p(a=1|c=1)p(b=1|c=1)\\
\therefore p(a,b|c)&=p(a|c)p(b|c)
\end{align*}
$$

Exercise (8.4)

$$
\begin{align*}
p(b=0|c=0)&=\frac{p(b=0,c=0)}{p(c=0)}\\
&=\frac{0.384}{0.48}\\
&=0.8\\
p(b=1|c=0)&=0.2\\
p(b=0|c=1)&=\frac{p(b=0,c=1)}{p(c=1)}\\
&=\frac{0.208}{0.52}\\
&=0.4\\
p(b=1|c=1)&=0.6\\
p(c=0|a=0)&=\frac{p(a=0,c=0)}{p(a=0)}\\
&=\frac{0.24}{0.6}\\
&=0.4\\
p(c=1|a=0)&=0.6\\
p(c=0|a=1)&=\frac{p(a=1,c=0)}{p(a=1)}\\
&=\frac{0.24}{0.4}\\
&=0.6\\
p(c=1|a=1)&=0.4\\
p(a=0,b=0,c=0)&=0.192\\
&=0.6*0.4*0.8\\
&=p(a=0)p(c=0|a=0)p(b=0|c=0)\\
p(a=0,b=0,c=1)&=0.144\\
&=0.6*0.6*0.4\\
&=p(a=0)p(c=1|a=0)p(b=0|c=1)\\
p(a=0,b=1,c=0)&=0.048\\
&=0.6*0.4*0.2\\
&=p(a=0)p(c=0|a=0)p(b=1|c=0)\\
p(a=0,b=1,c=1)&=0.216\\
&=0.6*0.6*0.6\\
&=p(a=0)p(c=1|a=0)p(b=1|c=1)\\
p(a=1,b=0,c=0)&=0.192\\
&=0.4*0.6*0.8\\
&=p(a=1)p(c=0|a=1)p(b=0|c=0)\\
p(a=1,b=0,c=1)&=0.064\\
&=0.4*0.4*0.4\\
&=p(a=1)p(c=1|a=1)p(b=0|c=1)\\
p(a=1,b=1,c=0)&=0.048\\
&=0.4*0.6*0.2\\
&=p(a=1)p(c=0|a=1)p(b=1|c=0)\\
p(a=1,b=1,c=1)&=0.096\\
&=0.4*0.4*0.6\\
&=p(a=1)p(c=1|a=1)p(b=1|c=1)\\
\therefore p(a,b,c)&=p(a)p(c|a)p(b|c)
\end{align*}
$$

Exercise (8.5)

Directed graph corresponding to eqn. (7.79) and (7.80)

Exercise (8.6)

まずは$${\mu_0=0}$$の場合を考える。
このとき，

$$
\begin{align*}
p(y=1|\mathbf{x})&=0 &\text{if } \mathbf{x}=\mathbf{0} \\
&\neq 0 &\text{other } \\
\end{align*}
$$

となり，$${\mathbf{x}}$$に0ではない成分が1つでも含まれていると$${p(y=1|\mathbf{x})}$$が0ではない有限値を有する。
まずは$${\mu_0\neq 0}$$の場合は，$${p(y=1|\mathbf{x}=\mathbf{0})(=\mu_0)}$$も0ではない有限値を有することになる。

Exercise (8.7)

$$
\begin{align*}
\mu_1&=\mathbb{E}[x_1]\\
&=b_1\\
\mu_2&=\mathbb{E}[x_2]\\
&=w_{21}\mathbb{E}[x_1]+b_2\\
&=b_2+w_{21}b_1\\
\mu_3&=\mathbb{E}[x_3]\\
&=w_{32}\mathbb{E}[x_2]+b_3\\
&=b_3+w_{32}b_2+w_{32}w_{21}b_1\\
\therefore \boldsymbol\mu &=\begin{pmatrix}b_1 & b_2+w_{21}b_1 & b_3+w_{32}b_2+w_{32}w_{21}b_1 \end{pmatrix}^{\rm T}
\end{align*}
$$

$$
\begin{align*}
{\rm cov}[x_1, x_1]&=v_1\\
{\rm cov}[x_1, x_2]&=w_{21}{\rm cov}[x_1, x_1]\\
&=w_{21}v_1\\
{\rm cov}[x_1, x_3]&=w_{32}{\rm cov}[x_1, x_2]\\
&=w_{32}w_{21}v_1\\
{\rm cov}[x_2, x_2]&=w_{21}{\rm cov}[x_2, x_1]+v_2\\
&=v_2+w_{21}^2v_1\\
{\rm cov}[x_2, x_3]&=w_{32}{\rm cov}[x_2, x_2]\\
&=w_{32}(v_2+w_{21}^2v_1)\\
{\rm cov}[x_3, x_3]&=w_{32}{\rm cov}[x_3, x_2]+v_3\\
&=v_3+w_{32}^2(v_2+w_{21}^2v_1)\\
\therefore \boldsymbol\Sigma&=\begin{pmatrix}v_1& w_{21}v_1& w_{32}w_{21}v_1\\ w_{21}v_1 & v_2+w_{21}^2v_1 & w_{32}(v_2+w_{21}^2v_1) \\ w_{32}w_{21}v_1 & w_{32}(v_2+w_{21}^2v_1) & v_3+w_{32}^2(v_2+w_{21}^2v_1)\end{pmatrix}
\end{align*}
$$

Exercise (8.8)

$$
\begin{align*}
p(a,b|d)&=\int{\rm d}cp(a,b,c|d)\\
&=\int{\rm d}cp(a|d)p(b,c|d)\\
&\ \ \ \ \ \ \ (\because a \perp\!\!\!\perp b,c|d)\\
&=p(a|d)\int{\rm d}cp(b,c|d)\\
&=p(a|d)p(b|d)\\
\end{align*}
$$

以上より，$${ a \perp\!\!\!\perp b,c|d}$$のとき$${ a \perp\!\!\!\perp b|d}$$が成立する。

Exercise (8.9)

Markov blanketの左側に着目し，周りのnode含め以下の図の通りnode名を付けて考えることにする。

$${x_2\rightarrow x_1 \rightarrow x_i}$$に着目すると，head-to-tail nodeである$${x_1}$$が観測されているので$${x_2}$$と$${x_i}$$はblockされている。
$${x_3\rightarrow x_1 \rightarrow x_i}$$に着目すると，tail-to-tail nodeである$${x_1}$$が観測されているので$${x_3}$$と$${x_i}$$はblockされている。
$${x_i\rightarrow x_7 \rightarrow x_8}$$に着目すると，head-to-tail nodeである$${x_7}$$が観測されているので$${x_8}$$と$${x_i}$$はblockされている。
$${x_5\rightarrow x_4\rightarrow x_7}$$に着目すると，head-to-tail nodeである$${x_4}$$が観測されているので$${x_5}$$と$${x_7}$$はblockされている。そのため，$${x_5}$$と$${x_i}$$もblockされている。
$${x_6\rightarrow x_4\rightarrow x_7}$$に着目すると，tail-to-tail nodeである$${x_4}$$が観測されているので$${x_6}$$と$${x_7}$$はblockされている。そのため，$${x_6}$$と$${x_i}$$もblockされている。

Markov blanketの右側も同様のことが言える。以上より，$${x_i}$$はMarkov blanketの外側のnodeに対してblockされている。

Exercise (8.10)

$${p(a,b,c,d)=p(a)p(b)p(c|a,b)p(d|c)}$$のとき，

$$
\begin{align*}
p(a,b)&=\sum_c\sum_d p(a,b,c,d)\\
&=\sum_c\sum_d p(a)p(b)p(c|a,b)p(d|c)\\
&=p(a)p(b)\sum_c p(c|a,b)\sum_d p(d|c)\\
&=p(a)p(b)\sum_c p(c|a,b)\\
&=p(a)p(b)\\
\therefore a &\perp\!\!\!\perp b,c|\emptyset
\end{align*}
$$

$$
\begin{align*}
p(a,b|d)&=\sum_c\frac{p(a,b,c,d)}{p(d)}\\
&=\sum_c \frac{p(a)p(b)p(c|a,b)p(d|c)}{p(d)}\\
&=p(a|d)p(b)\sum_c p(c|a,b)p(d|c)\\
&\neq p(a|d)p(b|d)\\
\therefore a&{\perp\!\!\!\perp}\mathllap{/\,} b|d
\end{align*}
$$

Exercise (8.11) - (8.20)

Exercise (8.11)

$${p(B,D, F,G)=p(B)p(F)p(G|B,F)p(D|G)}$$のとき，

$$
\begin{align*}
p(F=0|D=0)&=\sum_{B\in\{0,1\}}\sum_{G\in\{0,1\}}p(F=0,B,G|D=0)\\
&=\frac{\sum_{B\in\{0,1\}}\sum_{G\in\{0,1\}}p(B,D=0,F=0,G)}{p(D=0)}\\
&=\frac{\sum_{B\in\{0,1\}}\sum_{G\in\{0,1\}}p(B)p(F=0)p(G|B,F=0)p(D=0|G)}{p(D=0)}\\
&=\frac{p(F=0)\sum_{B\in\{0,1\}}p(B)\sum_{G\in\{0,1\}}p(G|B,F=0)p(D=0|G)}{p(D=0)}
\end{align*}
$$

となる。

$$
\begin{align*}
p(F=0)&=1-p(F=1)\\
&=1-0.9\\
&=0.1\\
p(D=0)&=\sum_{G\in\{0,1\}}p(D=0|G)p(G)\\
&=p(D=0|G=0)p(G=0)+p(D=0|G=1)p(G=1)\\
&=0.9\times 0.315+0.1\times 0.685\\
&=0.352\\
\sum_{G\in\{0,1\}}p(G|B=0,F=0)p(D=0|G)&=p(G=0|B=0,F=0)p(D=0|G=0)+p(G=1|B=0,F=0)p(D=0|G=1)\\
&=0.9\times 0.9+0.1\times 0.1\\
&=0.82\\
\sum_{G\in\{0,1\}}p(G|B=1,F=0)p(D=0|G)&=p(G=0|B=1,F=0)p(D=0|G=0)+p(G=1|B=1,F=0)p(D=0|G=1)\\
&=0.8\times 0.9+0.2\times 0.1\\
&=0.74
\end{align*}
$$

より，

$$
\begin{align*}
p(F=0|D=0)&=\frac{0.1\times \{p(B=0)\times 0.82 + p(B=1)\times 0.74\}}{0.352}\\
&=\frac{0.1\times (0.1\times 0.82 + 0.9\times 0.74)}{0.352}\\
&=0.2125
\end{align*}
$$

$$
\begin{align*}
p(F=0|B=0, D=0)&=\sum_{G\in\{0,1\}}p(F=0,G|B=0, D=0)\\
&=\frac{\sum_{G\in\{0,1\}}p(B,D=0,F=0,G)}{p(B=0, D=0)}\\
&=\frac{\sum_{G\in\{0,1\}}p(B=0)p(F=0)p(G|B=0,F=0)p(D=0|G)}{p(B=0, D=0)}\\
&=\frac{p(B=0)p(F=0)\sum_{G\in\{0,1\}}p(G|B=0,F=0)p(D=0|G)}{p(B=0, D=0)}
\end{align*}
$$

を計算することを考える。

$$
\begin{align*}
p(B=0, D=0)&=\sum_{F\in\{0,1\}}\sum_{G\in\{0,1\}}p(B=0, D=0, F, G)\\
&=p(B=0)\sum_{F\in\{0,1\}}p(F)\sum_{G\in\{0,1\}}p(G|B=0,F)p(D=0|G)\\
&=0.1\times\{0.1\times(0.9\times 0.9+0.1\times 0.1)+0.9\times(0.8\times 0.9+0.2\times 0.1)\}\\
&=0.0748
\end{align*}
$$

より，

$$
\begin{align*}
p(F=0|B=0, D=0)
&=\frac{0.1\times 0.1 \times 0.82}{0.0748}\\
&\simeq 0.11 (<p(F=0|D=0))
\end{align*}
$$

となる。
Exercise (8.10)の結果より，$${D}$$が測定されると$${B}$$と$${F}$$がunblockされるため，$${B}$$の測定が$${F}$$の条件付き確率に影響を及ぼする状態となる。
$${B=0}$$が確定すると$${F=0}$$の確率が下がるのは直感的には妥当である。

Exercise (8.12)

$${M}$$個の確率変数から２個を選ぶ組み合わせ数は$${\binom{M}{2}=M(M-1)/2 }$$ある。
それぞれの組み合わせに対して，接続が有無の2種類があるため，undirected graphの種類は$${2^{M(M-1)/2}}$$個存在する。

Exercise (8.13)

$${x_j=1}$$と$${x_j=-1}$$のエネルギーの差分を$${{\rm d}E_j}$$とおくと，

$$
\begin{align*}
{\rm d}E_j&=\left(h-\beta\sum_ix_i-\eta y_j\right)-\left(-h+\beta\sum_ix_i+\eta y_j\right)\\
&=2\left(h-\beta\sum_ix_i-\eta y_j\right)
\end{align*}
$$

となる。ここで，$${i}$$はnode $${j}$$と隣り合うnodeの番号を表す。

Exercise (8.14)

$${\beta=h=0}$$のとき，

$$
\begin{align*}
p(\mathbf{x},\mathbf{y})&=\frac{1}{Z}\exp\left(\eta\sum_i x_iy_i\right)\\
&=\frac{1}{Z}\prod_i\exp\left(\eta x_iy_i\right)
\end{align*}
$$

となる。各$${i}$$に対して$${ x_i=y_i}$$となる場合，確率が最大化される。

Exercise (8.15)

$$
\begin{align*}
p(x_{n-1},x_n)&=\sum_{x_1}\cdots\sum_{x_{n-2}}\sum_{x_{n+1}}\cdots\sum_{x_N}p(\mathbf{x})\\
&=\frac{1}{Z}\sum_{x_1}\cdots\sum_{x_{n-2}}\sum_{x_{n+1}}\cdots\sum_{x_N}\psi_{1,2}(x_1,x_2)\cdots\psi_{N-1,N}(x_{N-1},x_N)\\
&=\frac{1}{Z}\left[\left\{\sum_{x_{n-2}}\psi_{n-2,n-1}(x_{n-2},x_{n-1})\cdots\sum_{x_{1}}\psi_{1,2}(x_{1},x_{2})\right\}\psi_{n-1,n}(x_{n-1},x_n)\left\{\sum_{x_{n+1}}\psi_{n,n+1}(x_{n},x_{n+1})\cdots\sum_{x_{N}}\psi_{N-1,N}(x_{N-1},x_{N})\right\}\right]\\
&=\frac{1}{Z}\left[\left\{\sum_{x_{n-2}}\psi_{n-2,n-1}(x_{n-2},x_{n-1})\cdots\sum_{x_{2}}\psi_{2,3}(x_{2},x_{3})\mu_{\alpha}(x_2)\right\}\psi_{n-1,n}(x_{n-1},x_n)\left\{\sum_{x_{n+1}}\psi_{n,n+1}(x_{n},x_{n+1})\cdots\sum_{x_{N-1}}\psi_{N-2,N-1}(x_{N-2},x_{N-1})\mu_{\beta}(x_{N-1})\right\}\right]\\
&\ \ \ \ \ \ \vdots\\
&=\frac{1}{Z}\left[\left\{\sum_{x_{n-2}}\psi_{n-2,n-1}(x_{n-2},x_{n-1})\mu_{\alpha}(x_{n-2})\right\}\psi_{n-1,n}(x_{n-1},x_n)\left\{\sum_{x_{n+1}}\psi_{n,n+1}(x_{n},x_{n+1})\mu_{\beta}(x_{n+1})\right\}\right]\\
&=\frac{1}{Z}\mu_{\alpha}(x_{n-1})\psi_{n-1,n}(x_{n-1},x_n)\mu_{\beta}(x_{n})
\end{align*}
$$

Exercise (8.16)

$$
\begin{align*}
p(x_N)&=\sum_{x_1}\cdots\sum_{x_{N-1}} p(\mathbf{x})\\
&=\frac{1}{Z}\sum_{x_1}\cdots\sum_{x_{N-1}}\psi_{1,2}(x_1,x_2)\cdots\psi_{N-1,N}(x_{N-1},x_N)\\
&=\frac{1}{Z}\sum_{x_{N-1}}\psi_{N-1,N}(x_{N-1},x_N)\cdots\sum_{x_1}\psi_{1,2}(x_1,x_2)\\
&=\frac{1}{Z}\sum_{x_{N-1}}\psi_{N-1,N}(x_{N-1},x_N)\cdots\sum_{x_2}\psi_{2,3}(x_2,x_3)\mu_{\alpha}(x_2)\\
&\ \ \ \ \ \ \vdots\\
&=\frac{1}{Z}\sum_{x_{N-1}}\psi_{N-1,N}(x_{N-1},x_N)\mu_{\alpha}(x_{N-1})\\
&=\frac{1}{Z}\mu_{\alpha}(x_{N})
\end{align*}
$$

$$
\begin{align*}
p(x_n, x_N)&=\sum_{x_1}\cdots\sum_{x_{n-1}}\sum_{x_{n+1}}\cdots\sum_{x_{N-1}} p(\mathbf{x})\\
&=\frac{1}{Z}\sum_{x_1}\cdots\sum_{x_{n-1}}\sum_{x_{n+1}}\cdots\sum_{x_{N-1}}\psi_{1,2}(x_1,x_2)\cdots\psi_{N-1,N}(x_{N-1},x_N)\\
&=\frac{\mu_{\alpha}(x_n)}{Z}\sum_{x_{n+1}}\psi_{n,n+1}(x_{n},x_{n+1})\cdots\sum_{x_{N-1}}\psi_{N-2,N-1}(x_{N-2},x_{N-1})\psi_{N-1,N}(x_{N-1},x_N)\\
&=:\frac{\mu_{\alpha}(x_n)}{Z}\sum_{x_{n+1}}\psi_{n,n+1}(x_{n},x_{n+1})\cdots\sum_{x_{N-1}}\psi_{N-2,N-1}(x_{N-2},x_{N-1})\mu_{\beta}'(x_{N-1},x_N)\\
&\ \ \ \ \ \ \left(\mu_{\beta}'(x_{N-1},x_N):=\psi_{N-1,N}(x_{N-1},x_N)\right)\\
&=:\frac{\mu_{\alpha}(x_n)}{Z}\sum_{x_{n+1}}\psi_{n,n+1}(x_{n},x_{n+1})\cdots\sum_{x_{N-2}}\psi_{N-3,N-2}(x_{N-3},x_{N-2})\mu_{\beta}'(x_{N-2},x_N)\\
&\ \ \ \ \ \ \left(\mu_{\beta}'(x_{N-2},x_N):=\sum_{x_{N-1}}\psi_{N-2,N-1}(x_{N-2},x_{N-1})\mu_{\beta}'(x_{N-1},x_N)\right)\\
&\ \ \ \ \ \ \vdots\\
&=\frac{\mu_{\alpha}(x_n)}{Z}\sum_{x_{n+1}}\psi_{n,n+1}(x_{n},x_{n+1})\mu_{\beta}'(x_{n+1},x_N)\\
&=\frac{\mu_{\alpha}(x_n)\mu_{\beta}'(x_{n},x_N)}{Z}
\end{align*}
$$

$$
\begin{align*}
\therefore p(x_n|x_N)&=\frac{p(x_n, x_N)}{p(x_N)}\\
&=\frac{\mu_{\alpha}(x_n)\mu_{\beta}'(x_{n},x_N)}{\mu_{\alpha}(x_{N})}
\end{align*}
$$

Exercise (8.17)

Figure (8.38)に対応するdirected graphを考える。
$${x_2\rightarrow x_3\rightarrow x_4}$$の部分において，head to tail nodeである$${x_3}$$が観測されると，$${x_2}$$と$${x_4}$$がblockされる。そのため，$${x_2 \perp\!\!\!\perp x_5|x_3}$$となる。

$$
\begin{align*}
p(x_2|x_3,x_5)&=\frac{p(x_2, x_3,x_5)}{p(x_3,x_5)}\\
&=\frac{\sum_{x_1}\sum_{x_4}p(\mathbf{x})}{\sum_{x_1}\sum_{x_2}\sum_{x_4}p(\mathbf{x})}\\
&=\frac{\left\{\sum_{x_1}\psi_{1,2}(x_1,x_2)\right\}\psi_{2,3}(x_2,x_3)\left\{\sum_{x_4}\psi_{3,4}(x_3,x_4)\psi_{4,5}(x_4,x_5)\right\}}{\left\{\sum_{x_2}\psi_{2,3}(x_2,x_3)\sum_{x_1}\psi_{1,2}(x_1,x_2)\right\}\left\{\sum_{x_4}\psi_{3,4}(x_3,x_4)\psi_{4,5}(x_4,x_5)\right\}}\\
&=\frac{\left\{\sum_{x_1}\psi_{1,2}(x_1,x_2)\right\}\psi_{2,3}(x_2,x_3)}{\left\{\sum_{x_2}\psi_{2,3}(x_2,x_3)\sum_{x_1}\psi_{1,2}(x_1,x_2)\right\}}\\
&=\frac{\mu_{\alpha}(x_2)\psi_{2,3}(x_2,x_3)}{\sum_{x_2}\psi_{2,3}(x_2,x_3)\mu_{\alpha}(x_2)}\\
&=\frac{\mu_{\alpha}(x_2)\psi_{2,3}(x_2,x_3)}{\mu_{\alpha}(x_3)}\\
\end{align*}
$$

となり，$${p(x_2|x_3,x_5)}$$は$${x_5}$$に依存しない。

Exercise (8.18)

以下のdirected treeをundirected treeに変換することを考える。

$$
\begin{align*}
p(\mathbf{x})&=p(x_1)p(x_2|x_1)p(x_3|x_1)p(x_2|x_4)p(x_5|x_2)p(x_6|x_3)p(x_7|x_3)\\
&=\psi_{1,2}(x_1,x_2)\psi_{1,3}(x_1,x_3)\psi_{2,4}(x_2,x_4)\psi_{2,5}(x_2,x_5)\psi_{3,6}(x_3,x_6)\psi_{3,7}(x_3,x_7)\\\\
\psi_{1,2}(x_1,x_2)&:=p(x_1)p(x_2|x_1)\\
\psi_{1,3}(x_1,x_3)&:=p(x_3|x_1)\\
\psi_{2,4}(x_2,x_4)&:=p(x_2|x_4)\\
\psi_{2,5}(x_2,x_5)&:=p(x_5|x_2)\\
\psi_{3,6}(x_3,x_6)&:=p(x_6|x_3)\\
\psi_{3,7}(x_3,x_7)&:=p(x_7|x_3)\\
\end{align*}
$$

となり，以下の図に対応するundirected treeに変換できる。

次に以下のundirected treeをdirected treeに変換することを考える。

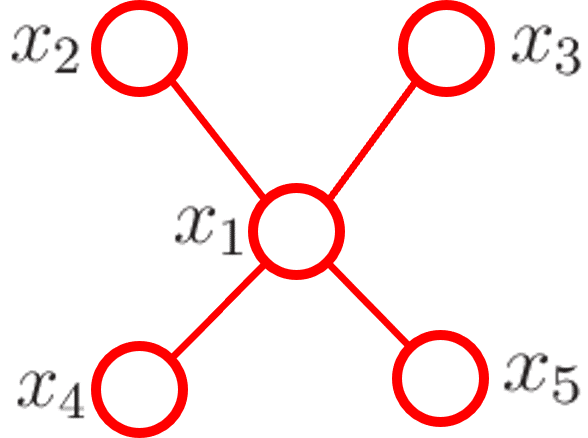
$$
\begin{align*}
p(\mathbf{x})&=\frac{\psi_{1,2}(x_1,x_2)\psi_{1,3}(x_1,x_3)\psi_{1,4}(x_1,x_4)\psi_{1,5}(x_1,x_5)}{\sum_{\mathbf{x}}\psi_{1,2}(x_1,x_2)\psi_{1,3}(x_1,x_3)\psi_{1,4}(x_1,x_4)\psi_{1,5}(x_1,x_5)}\\
&=\frac{\psi_{1,2}(x_1,x_2)\psi_{1,3}(x_1,x_3)\psi_{1,4}(x_1,x_4)\sum_{x_5}\psi_{1,5}(x_1,x_5)}{\sum_{\mathbf{x}}\psi_{1,2}(x_1,x_2)\psi_{1,3}(x_1,x_3)\psi_{1,4}(x_1,x_4)\psi_{1,5}(x_1,x_5)}\frac{\psi_{1,5}(x_1,x_5)}{\sum_{x_5}\psi_{1,5}(x_1,x_5)}\\
&=\frac{\psi_{1,2}(x_1,x_2)\psi_{1,3}(x_1,x_3)\sum_{x_4, x_5}\psi_{1,4}(x_1,x_4)\psi_{1,5}(x_1,x_5)}{\sum_{\mathbf{x}}\psi_{1,2}(x_1,x_2)\psi_{1,3}(x_1,x_3)\psi_{1,4}(x_1,x_4)\psi_{1,5}(x_1,x_5)}\frac{\psi_{1,4}(x_1,x_4)}{\sum_{x_4}\psi_{1,4}(x_1,x_4)}\frac{\psi_{1,5}(x_1,x_5)}{\sum_{x_5}\psi_{1,5}(x_1,x_5)}\\
&=\frac{\psi_{1,2}(x_1,x_2)\sum_{x_3, x_4, x_5}\psi_{1,3}(x_1,x_3)\psi_{1,4}(x_1,x_4)\psi_{1,5}(x_1,x_5)}{\sum_{\mathbf{x}}\psi_{1,2}(x_1,x_2)\psi_{1,3}(x_1,x_3)\psi_{1,4}(x_1,x_4)\psi_{1,5}(x_1,x_5)}\frac{\psi_{1,3}(x_1,x_3)}{\sum_{x_3}\psi_{1,3}(x_1,x_3)}\frac{\psi_{1,4}(x_1,x_4)}{\sum_{x_4}\psi_{1,4}(x_1,x_4)}\frac{\psi_{1,5}(x_1,x_5)}{\sum_{x_5}\psi_{1,5}(x_1,x_5)}\\
&=\frac{\sum_{x_2,x_3, x_4, x_5}\psi_{1,2}(x_1,x_2)\psi_{1,3}(x_1,x_3)\psi_{1,4}(x_1,x_4)\psi_{1,5}(x_1,x_5)}{\sum_{\mathbf{x}}\psi_{1,2}(x_1,x_2)\psi_{1,3}(x_1,x_3)\psi_{1,4}(x_1,x_4)\psi_{1,5}(x_1,x_5)}\frac{\psi_{1,2}(x_1,x_2)}{\sum_{x_2}\psi_{1,2}(x_1,x_2)}\frac{\psi_{1,3}(x_1,x_3)}{\sum_{x_3}\psi_{1,3}(x_1,x_3)}\frac{\psi_{1,4}(x_1,x_4)}{\sum_{x_4}\psi_{1,4}(x_1,x_4)}\frac{\psi_{1,5}(x_1,x_5)}{\sum_{x_5}\psi_{1,5}(x_1,x_5)}\\
&=p(x_1)p(x_2|x_1)p(x_3|x_1)p(x_4|x_1)p(x_5|x_1)\\\\
p(x_1)&:=\frac{\sum_{x_2,x_3, x_4, x_5}\psi_{1,2}(x_1,x_2)\psi_{1,3}(x_1,x_3)\psi_{1,4}(x_1,x_4)\psi_{1,5}(x_1,x_5)}{\sum_{\mathbf{x}}\psi_{1,2}(x_1,x_2)\psi_{1,3}(x_1,x_3)\psi_{1,4}(x_1,x_4)\psi_{1,5}(x_1,x_5)}\\
p(x_2|x_1)&:=\frac{\psi_{1,2}(x_1,x_2)}{\sum_{x_2}\psi_{1,2}(x_1,x_2)}\\
p(x_3|x_1)&:=\frac{\psi_{1,3}(x_1,x_3)}{\sum_{x_3}\psi_{1,3}(x_1,x_3)}\\
p(x_4|x_1)&:=\frac{\psi_{1,4}(x_1,x_4)}{\sum_{x_4}\psi_{1,4}(x_1,x_4)}\\
p(x_5|x_1)&:=\frac{\psi_{1,5}(x_1,x_5)}{\sum_{x_5}\psi_{1,5}(x_1,x_5)}\\
\end{align*}
$$

となり，以下の図に対応するdirected graphに変換できる。

式変形は他にも以下のようにすることもできる。

これは以下のdirected graphと等価である。

このようにundirected treeをdirected treeに変換する際，任意のnodeをrootに指定できるため，undirected treeに対応するdirected treeはnode数だけ存在する。

Exercise (8.19)

$$
\begin{align*}
\mu_{x_1\rightarrow\psi_{1,2}}(x_1)&=1\\
\mu_{\psi_{1,2}\rightarrow x_2}(x_2)&=\sum_{x_1}\psi_{1,2}(x_1,x_2)\mu_{x_1\rightarrow\psi_{1,2}}(x_1)\\
&=\sum_{x_1}\psi_{1,2}(x_1,x_2)\\
&=\mu_{\alpha}(x_2)\\
\mu_{x_2\rightarrow\psi_{2,3}}(x_2)&=\mu_{\psi_{1,2}\rightarrow x_2}(x_2)\\
&=\mu_{\alpha}(x_2)\\
\mu_{\psi_{2,3}\rightarrow x_3}(x_3)&=\sum_{x_2}\psi_{2,3}(x_2,x_3)\mu_{x_2\rightarrow\psi_{2,3}}(x_2)\\
&=\sum_{x_2}\psi_{2,3}(x_2,x_3)\mu_{\alpha}(x_2)\\
&=\mu_{\alpha}(x_3)\\
&\vdots\\
\mu_{\psi_{n-1,n}\rightarrow x_n}(x_n)&=\sum_{x_{n-1}}\psi_{n-1,n}(x_{n-1},x_n)\mu_{x_{n-1}\rightarrow\psi_{n-1,n}}(x_{n-1})\\
&=\sum_{x_{n-1}}\psi_{n-1,n}(x_{n-1},x_n)\mu_{\alpha}(x_{n-1})\\
&=\mu_{\alpha}(x_n)
\end{align*}
$$

$$
\begin{align*}
\mu_{x_N\rightarrow\psi_{N,N-1}}(x_N)&=1\\
\mu_{\psi_{N,N-1}\rightarrow x_{N-1}}(x_{N-1})&=\sum_{x_N}\psi_{N-1,N}(x_{N-1},x_N)\mu_{x_N\rightarrow\psi_{N,N-1}}(x_N)\\
&=\sum_{x_N}\psi_{N-1,N}(x_{N-1},x_N)\\
&=\mu_{\beta}(x_{N-1})\\
\mu_{x_{N-1}\rightarrow\psi_{N-2,N-1}}(x_{N-1})&=\mu_{\psi_{N,N-1}\rightarrow x_{N-1}}(x_{N-1})\\
&=\mu_{\beta}(x_{N-1})\\
\mu_{\psi_{N-2,N-1}\rightarrow x_{N-2}}(x_{N-2})&=\sum_{x_{N-1}}\psi_{N-2,N-1}(x_{N-2},x_{N-1})\mu_{x_{N-1}\rightarrow\psi_{N-2,N-1}}(x_{N-1})\\
&=\sum_{x_{N-1}}\psi_{N-2,N-1}(x_{N-2},x_{N-1})\mu_{\beta}(x_{N-1})\\
&=\mu_{\beta}(x_{N-2})\\
&\vdots\\
\mu_{\psi_{n,n+1}\rightarrow x_{n}}(x_{n})&=\sum_{x_{n+1}}\psi_{n,n+1}(x_{n},x_{n+1})\mu_{x_{n+1}\rightarrow\psi_{n,n+1}}(x_{n+1})\\
&=\sum_{x_{n+1}}\psi_{n,n+1}(x_{n},x_{n+1})\mu_{\beta}(x_{n+1})\\
&=\mu_{\beta}(x_n)\\
\end{align*}
$$

以上より，題意は示された。

Exercise (8.20)

$${N=1}$$のnode数を有するtree graphの場合，そのnodeをrootとすると，rootにメッセージ伝達するleaf node及びrootからメッセージ伝達されるleaf nodeがそもそも存在しないので，題意が成立することは自明である。

$${N=k}$$のnode数を有するtree graphで題意が成立すると仮定する。
また，$${N=k+1}$$のnode数を有するtree graphは，$${N=k}$$の場合に新たにleaf nodeを生やして構築されたものを考えることにする。
新たに生やされたleaf nodeからroot nodeへの伝達を考える場合，leaf nodeが受け取るメッセージはないため，まずleaf nodeからleaf nodeのparent nodeにメッセージが伝達される。leaf nodeのparent nodeは元の$${N=k}$$のnode数を有するtree graphに含まれているnodeであるため，それ以降のroot nodeへの伝達は題意を満たす。
また，root nodeから各leaf nodeへの伝達を考える場合，新たに生やされたleaf nodeへの伝達はそのparent nodeが受けるべき全てのメッセージを受け取ってから実施される。そのため，$${N=k+1}$$の場合も題意が成立する。
以上より，任意の$${N(\geq 1)}$$において題意が成立する。

Exercise (8.21) - (8.29)

Exercise (8.21)

$$
\begin{align*}
p(\mathbf{x}_s)&=\sum_{\mathbf{x}\backslash \mathbf{x}_s}p(\mathbf{x})\\
&=\sum_{\mathbf{x}\backslash \mathbf{x}_s}\left\{\prod_{s'}f_{s'}(\mathbf{x}_{s'})\right\}\\
&=f_{s}(\mathbf{x}_{s})\sum_{\mathbf{x}\backslash \mathbf{x}_s}\left\{\prod_{s'\backslash s}f_{s'}(\mathbf{x}_{s'})\right\}\\
&=f_{s}(\mathbf{x}_{s})\sum_{\mathbf{x}\backslash \mathbf{x}_s}\left\{\prod_{x_i\in{\rm ne}(f_s)}G_i(x_i,X_{si})\right\}\\
&=f_{s}(\mathbf{x}_{s})\prod_{x_i\in{\rm ne}(f_s)}\left\{\sum_{X_{si}}G_i(x_i,X_{si})\right\}\\
&=f_{s}(\mathbf{x}_{s})\prod_{x_i\in{\rm ne}(f_s)}\mu_{x_i\rightarrow f_{s}}(x_i)
\end{align*}
$$

Exercise (8.22)

対象とするsubgraphに含まれるfactor nodeのindexを$${t}$$で表すことにする。
また，$${f_t}$$と直接繋がっているvariable nodeを$${\mathbf{x}_t}$$，subgraphに含まれるvariable node全体を$${\mathbf{x}_T}$$とする。
このとき，

$$
\begin{align*}
p(\mathbf{x}_T)&=\sum_{\mathbf{x}\backslash \mathbf{x}_T}p(\mathbf{x})\\
&=\sum_{\mathbf{x}\backslash \mathbf{x}_T}\left\{\prod_{s'}f_{s'}(\mathbf{x}_{s'})\right\}\\
&=\left\{\prod_{t}f_{t}(\mathbf{x}_{t})\right\}\sum_{\mathbf{x}\backslash \mathbf{x}_T}\left\{\prod_{s' \backslash t}f_{s'}(\mathbf{x}_{s'})\right\}\\
&=\left\{\prod_{t}f_{t}(\mathbf{x}_{t})\right\}\sum_{\mathbf{x}\backslash \mathbf{x}_T}\left\{\prod_{x_i\in \mathbf{x}_T}\prod_{s\in {\rm ne}(x_i)\backslash f_t}F_s(x_i,X_s)\right\}\\
&=\left\{\prod_{t}f_{t}(\mathbf{x}_{t})\right\}\prod_{x_i\in \mathbf{x}_T}\prod_{s\in {\rm ne}(x_i) \backslash f_t}\left\{\sum_{X_s}F_s(x_i,X_s)\right\}\\
&=\left\{\prod_{t}f_{t}(\mathbf{x}_{t})\right\}\prod_{x_i\in \mathbf{x}_T}\prod_{s\in {\rm ne} (x_i)\backslash f_t}\mu_{f_s\rightarrow x_i}(x_i)\\
\end{align*}
$$

Exercise (8.23)

$$
\begin{align*}
p(x)&=\prod_{s\in{\rm ne}(x)}\mu_{f_s\rightarrow x}(x)\\
&=\mu_{f_s\rightarrow x}(x)\prod_{l\in{\rm ne}(x)\backslash f_s}\mu_{f_l\rightarrow x}(x)\\
&=\mu_{f_s\rightarrow x}(x)\mu_{x\rightarrow f_s}(x)
\end{align*}
$$

最後の式変形には文中の式(8.69)を用いた。
以上より，題意は示された。

Exercise (8.24)

Exercise (8.21)と問われていることの違いが良く分からないため，省略

Exercise (8.25)

$$
\begin{align*}
\widetilde{p}(x_1)&=\mu_{f_a\rightarrow x_1}(x_1)\\
&=\sum_{x_2}f_a(x_1,x_2)\mu_{x_2\rightarrow f_a}(x_2)\\
&=\sum_{x_2}f_a(x_1,x_2)\mu_{f_b\rightarrow x_2}(x_2)\mu_{f_c\rightarrow x_2}(x_2)\\
&=\sum_{x_2}f_a(x_1,x_2)\sum_{x_3}f_b(x_2,x_3)\sum_{x_4}f_c(x_2,x_4)\\
&=\sum_{x_2}\sum_{x_3}\sum_{x_4}f_a(x_1,x_2)f_b(x_2,x_3)f_c(x_2,x_4)\\
&=\sum_{\mathbf{x}\backslash x_1}\widetilde{p}(\mathbf{x})
\end{align*}
$$

$$
\begin{align*}
\widetilde{p}(x_3)&=\mu_{f_b\rightarrow x_3}(x_3)\\
&=\sum_{x_2}f_b(x_2,x_3)\mu_{x_2\rightarrow f_b}(x_2)\\
&=\sum_{x_2}f_b(x_2,x_3)\mu_{f_a\rightarrow x_2}(x_2)\mu_{f_c\rightarrow x_2}(x_2)\\
&=\sum_{x_2}f_b(x_2,x_3)\sum_{x_1}f_a(x_1,x_2)\sum_{x_4}f_c(x_2,x_4)\\
&=\sum_{x_1}\sum_{x_2}\sum_{x_4}f_a(x_1,x_2)f_b(x_2,x_3)f_c(x_2,x_4)\\
&=\sum_{\mathbf{x}\backslash x_3}\widetilde{p}(\mathbf{x})
\end{align*}
$$

$$
\begin{align*}
\widetilde{p}(x_1,x_2)&=f_a(x_1,x_2)\prod_{i=1,2}\mu_{x_i\rightarrow f_a}(x_i)\\
&=f_a(x_1,x_2)\mu_{x_1\rightarrow f_a}(x_1)\mu_{x_2\rightarrow f_a}(x_2)\\
&=f_a(x_1,x_2)\mu_{f_b\rightarrow x_2}(x_2)\mu_{f_c\rightarrow x_2}(x_2)\\
&=f_a(x_1,x_2)\sum_{x_3}f_b(x_2,x_3)\sum_{x_4}f_c(x_2,x_4)\\
&=\sum_{x_3,x_4}f_a(x_1,x_2)f_b(x_2,x_3)f_c(x_2,x_4)\\
&=\sum_{x_3,x_4}\widetilde{p}(\mathbf{x})
\end{align*}
$$

Exercise (8.26)

$${x_a\rightarrow x_b}$$のpathに含まれるfactor nodeをまとめて$${{\rm pa}(a\rightarrow b)}$$，$${{\rm pa}(a\rightarrow b)}$$に含まれて$${x_a,x_b}$$と接続するfactor nodeをそれぞれ$${f_a,f_b}$$，及び$${x_a\rightarrow x_b}$$のpathに含まれる$${x_a,x_b}$$以外のvariable nodeをまとめて$${X_{a\rightarrow b}}$$とする。
このとき，$${p(x_a, x_b)}$$は

$$
\begin{align*}
p(x_a,x_b)&=\mu_{x_a\rightarrow f_a}(x_a)\mu_{x_b\rightarrow f_b}(x_b)\sum_{x_i\in X_{a\rightarrow b}}\left\{\prod_{s\in{\rm pa}(a\rightarrow b)}f_s(\mathbf{x_s})\right\}\left\{\prod_{t\in{\rm ne}(x_i)\backslash{\rm pa}(a\rightarrow b)}\mu_{f_t\rightarrow x_i}(x_i)\right\}
\end{align*}
$$

と表すことができる。

Exercise (8.27)

$${\widehat{x}=\widehat{y}=0}$$の場合を考える。
例えば，以下の確率の値を取るとき題意が満たされる。

$$
\begin{align*}
p(x=0,y=0)&=0\\
p(x=0,y=1)&=p(x=0,y=2)&=\frac{3}{16}\\
p(x=1,y=0)&=\frac{3}{16}\\
p(x=1,y=1)&=p(x=1,y=2)&=\frac{1}{16}\\
p(x=2,y=0)&=\frac{3}{16}\\
p(x=2,y=1)&=p(x=2,y=2)&=\frac{1}{16}\\
\end{align*}
$$

Exercise (8.28)

cycleを形成しているnodeは，少なくとも２つのnodeと接続していることになる。
そのため，cycle内のあるnodeからmessageが送信されたとき，受信先のnodeは送信元以外に接続しているnodeに対してpending messageを持っていることになる。

Exercise (8.29)

loop構造を有さないtree structure graphの場合，接続が一つしかないnodeが存在するため，そのnodeにmessageが送信されたときpending messageがない状態となる。

参考文献

Christopher Bishop, Pattern Recognition and Machine Learning

この記事が気に入ったらサポートをしてみませんか？