Statistical Mechanics: Theory and Molecular Simulation Chapter 2 - Theoretical foundations of classical statistical mechanics -

Statistical Mechanics: Theory and Molecular SimulationはMark Tuckermanによって著された分子シミュレーションに関連した熱・統計物理学，及び量子力学の参考書になります。

Amazon.co.jp: Statistical Mechanics: Theory and Molecular Simulation (Oxford Graduate Texts) : Tuckerman, Mark: Foreign Language Books

現時点では（恐らく）和訳がないこともあり，日本での知名度はあまりないような気がしますが，被引用数が1300を超えていることを考えると海外では高く認知されている参考書みたいです。

Mark E Tuckerman

本記事では，Chapter 2（Theoretical foundations of classical statistical mechanics）の章末問題の和訳とその解答例を紹介します。解答例に間違いが見受けられた場合はお知らせいただけると助かります。

Problem 2.1

体積$${V}$$，圧力$${P}$$，温度$${T}$$の熱力学条件下にある$${n}$$モルの理想気体を考える。状態方程式は式(2.2.2)にあるように$${PV=nRT}$$で与えられる。気体が$${N}$$個の分子を含むとすると，$${n=N/N_0}$$が成立する，ここで$${N_0}$$はアボガドロ数である。微視的状態の総数$${\Omega\propto V^N(kT)^{3N/2}}$$で与えられる（Section 3.5を参照），ここで$${k=R/N_0}$$はボルツマン定数である。また，この気体のエントロピー，及び全エネルギーはそれぞれ$${S=k\ln\Omega,\ E=3nRT/2}$$で与えられる。

a. 温度を一定に保った状態で体積を$${V_1}$$から$${V_2}$$に変化された際に系になされる仕事を計算せよ。

b. (a)の過程におけるエントロピー変化をボルツマンの関係式，及び式(2.2.19)を用いた場合でそれぞれ計算し，結果が一致することを確認せよ。

$$
\begin{align*}
\Delta S&=\int_1^2\frac{{\rm d}Q}{T}
\end{align*}\tag{2.2.19}
$$

c. 体積を一定に保った状態で温度を$${T_1}$$から$${T_2}$$に変化させる過程を考える。(b)と同様に２つのアプローチでエントロピー変化を計算し，結果が一致することを確認せよ。

d. 体積を$${V_1}$$から$${V_2}$$に断熱的($${\Delta Q=0}$$)に変化させる過程を考える。過程では圧力も$${P_1}$$から$${P_2}$$に変化するものとする。このとき，関係式

$$
\begin{align*}
P_1V_1^{\gamma}&=P_2V_2^{\gamma}
\end{align*}
$$

が成立することを示し，$${\gamma}$$の数値を決定せよ。

---

a. 

$$
\begin{align*}
W&=-\int_{V_1}^{V_2}{\rm d}VP\\
&=-nRT\int_{V_1}^{V_2}\frac{{\rm d}V}{V}\\
&=-nRT\ln\left(\frac{V_2}{V_1}\right)
\end{align*}
$$

b. (a)の過程のエントロピー変化をボルツマンの関係式を用いて計算すると，

$$
\begin{align*}
\Delta S&=k\ln\left(\frac{\Omega_2}{\Omega_1}\right)\\
&=Nk\ln\left(\frac{V_2}{V_1}\right)
\end{align*}
$$

となる。
一方，等温過程において内部エネルギーが変化しないことに注意すると，

$$
\begin{align*}
\Delta Q&=-W
\end{align*}
$$

が成立するため，式(2.2.19)を用いたエントロピー変化は

$$
\begin{align*}
\Delta S&=\frac{\Delta Q}{T}\\
&=-\frac{W}{T}\\
&=nR\ln\left(\frac{V_2}{V_1}\right)\\
&=\frac{N}{N_0}N_0k\ln\left(\frac{V_2}{V_1}\right)\\
&=Nk\ln\left(\frac{V_2}{V_1}\right)
\end{align*}
$$

と計算される。

c. 等積過程のエントロピー変化をボルツマンの関係式を用いて計算すると，

$$
\begin{align*}
\Delta S&=k\ln\left(\frac{\Omega_2}{\Omega_1}\right)\\
&=\frac{3Nk}{2}\ln\left(\frac{T_2}{T_1}\right)
\end{align*}
$$

となる。
一方，等積過程では$${W=0}$$より，

$$
\begin{align*}
{\rm d}Q&={\rm d}E\\
&=\frac{3}{2}nR{\rm d}T
\end{align*}
$$

となるため，式(2.2.19)を用いたエントロピー変化は

$$
\begin{align*}
\Delta S&=\int_1^2\frac{{\rm d}Q}{T}\\
&=\frac{3}{2}nR\int_{T_1}^{T_2}\frac{{\rm d}T}{T}\\
&=\frac{3}{2}nR\ln\left(\frac{T_2}{T_1}\right)\\
&=\frac{3Nk}{2}\ln\left(\frac{T_2}{T_1}\right)
\end{align*}
$$

と計算される。

d. $${{\rm d}Q=0}$$のとき，

$$
\begin{align*}
{\rm d}U&={\rm d}W\\
\therefore \frac{3}{2}nR{\rm d}T&=-P{\rm d}V
\end{align*}
$$

が成立する。
状態方程式の熱力学変数を微小変化させると，

$$
\begin{align*}
V{\rm d}P+P{\rm d}V&=nR{\rm d}T\\
&=-\frac{2}{3}P{\rm d}V\\
\frac{{\rm d}P}{P}+\frac{5}{3}\frac{{\rm d}V}{V}&=0\\
\ln P+\frac{5}{3}\ln V &={\rm const.}\\
PV^{\frac{5}{3}}&={\rm const.}\\
\therefore \gamma&=\frac{5}{3}
\end{align*}
$$

Problem 2.2

ある系が以下の性質を満たすとき，系の状態方程式，及びヘルムホルツの自由エネルギーを求めよ。
i. 等温膨張($${V_1\rightarrow V_2}$$)において系がする仕事は

$$
\begin{align*}
W&=RT\ln\left(\frac{V_2}{V_1}\right)
\end{align*}
$$

で与えられる。
ii. 体積が$${V_1\rightarrow V_2}$$，温度が$${T_1\rightarrow T_2}$$に変化する過程においてエントロピー変化が

$$
\begin{align*}
\Delta S&=k\ln\left\{\left(\frac{V_1}{V_2}\right)\left(\frac{T_2}{T_1}\right)^{\alpha}\right\}
\end{align*}
$$

で与えられる，ここで$${\alpha}$$はある定数である。

---

温度一定の条件では圧力は体積のみの関数と見なせるため，

$$
\begin{align*}
W&=RT\ln\left(\frac{V_2}{V_1}\right)\\
&=\int_{V_1}^{V_2}{\rm d}VP(V)\\
P(V_2)&=\frac{{\rm d}}{{\rm d}V_2}\int_{V_1}^{V_2}{\rm d}VP(V)\\
&=\frac{RT}{V_2}\\
\therefore PV-RT&=0
\end{align*}
$$

つまり，系は理想気体である。
$エントロピーが$${S(T,V)=k\ln\left\{\left(\frac{V_0}{V}\right)\left(\frac{T}{T_0}\right)^{\alpha}\right\}}$$で与えられること，及び理想気体の内部エネルギー$${U}$$は温度のみの関数となることを利用すると，

$$
\begin{align*}
U(T)&=\alpha k T
\end{align*}
$$

となる。
以上より，ヘルムホルツの自由エネルギー$${F(T,V)}$$は，

$$
\begin{align*}
F(T,V)&=\alpha kT-kT\ln\left\{\left(\frac{V_0}{V}\right)\left(\frac{T}{T_0}\right)^{\alpha}\right\}\\
&=kT\left[\alpha-\ln\left\{\left(\frac{V_0}{V}\right)\left(\frac{T}{T_0}\right)^{\alpha}\right\}\right]
\end{align*}
$$

となる。

Problem 2.3

理想気体に対するカルノーサイクルを$${P-V}$$平面ではなく$${T-S}$$平面上での熱力学サイクルとして描き，その熱力学サイクルで囲われる領域の面積がサイクル中に気体が外部に行う仕事に一致することを示せ。

---

熱力学サイクルは図１のようになる。

図１：T-S平面上での理想気体のカルノーサイクル

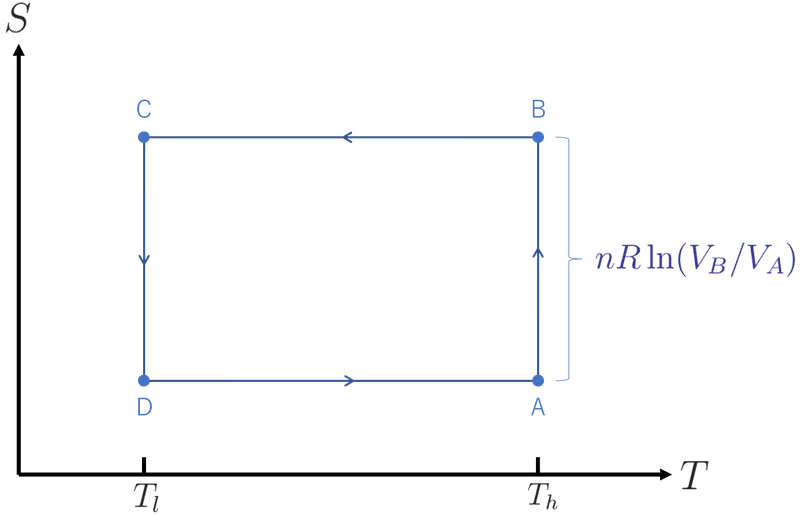
サイクルが囲う領域の面積は$${(T_h-T_l)\times nR\ln(V_B-V_A)}$$となる。

Problem 2.4

図2で示される熱力学サイクルを考える。この熱力学サイクルとカルノーエンジンの熱効率を比較せよ。どちらがより効率的か？

図２： 熱力学サイクル（参考文献より転載）

---

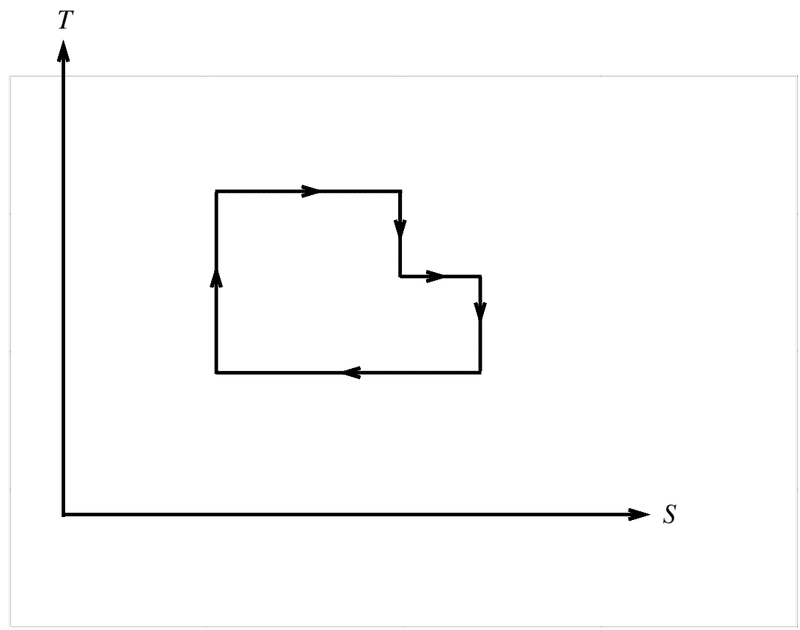
Problem 2.3で見たように，$${T-S}$$平面上でサイクルが囲う面積は系が外界にする仕事に等しい。そのため，サイクルの形状が長方形になるカルノーエンジンの方が，図２の熱力学サイクルより外界にする仕事が大きく，熱効率が高い。

Problem 2.5

以下の運動方程式に従う一次元系を時間発展する一粒子のアンサンブルを考える。

$$
\begin{align*}
\dot{x}&=-\alpha x
\end{align*}
$$

ここで，$${x(t)}$$は時間$${t}$$における粒子の位置であり，$${\alpha}$$は定数である。この系の圧縮率は0とならないため，アンサンブルの分布関数$${f(x,t)}$$は下記のリウヴィル方程式に従う。

$$
\begin{align*}
\frac{\partial f}{\partial t}-\alpha x\frac{\partial f}{\partial x}&=\alpha f
\end{align*}
$$

ここで，$${t=0}$$のときに分布関数がガウス型であったと仮定する。

$$
\begin{align*}
f(x,0)&=\frac{1}{\sqrt{2\pi\sigma^2}}{\rm e}^{-x^2/2\sigma^2}
\end{align*}
$$

a. この初期条件を満たすリウヴィル方程式の解を求めよ。まず，$${f(x,t)={\rm e}^{\alpha t}\tilde{f}(x,t)}$$とし，$${\tilde{f}(x,t)}$$が圧縮率0の場合のリウヴィル方程式に従うことを示せ。次に$${g(0)=1}$$を満たす$${g(x)}$$を指数の$${x^2}$$にかけ，$${g(t)}$$の具体的な表式を求めよ。

b. 分布関数の時間発展を定性的に描画し，なぜそのような挙動となるか説明せよ。

c. 解が確率分布としての規格化条件

$$
\begin{align*}
\int_{-\infty}^{\infty}{\rm d}xf(x,t)&=1
\end{align*}
$$

を満たすことを示せ。

---

a.

$$
\begin{align*}
\frac{\partial }{\partial t}\left({\rm e}^{\alpha t}\tilde{f}(x,t)\right)-\alpha x\frac{\partial }{\partial x}\left({\rm e}^{\alpha t}\tilde{f}(x,t)\right)&=\alpha \left({\rm e}^{\alpha t}\tilde{f}(x,t)\right)\\
\alpha{\rm e}^{\alpha t}\tilde{f}(x,t)+{\rm e}^{\alpha t}\frac{\partial \tilde{f}(x,t)}{\partial t}-\alpha x{\rm e}^{\alpha t}\frac{\partial \tilde{f}(x,t)}{\partial x}&=\alpha {\rm e}^{\alpha t}\tilde{f}(x,t)\\
\therefore \frac{\partial \tilde{f}(x,t)}{\partial t}-\alpha x\frac{\partial \tilde{f}(x,t)}{\partial x}&=0
\end{align*}
$$

$${\tilde{f}(x,t)=\exp(-\frac{g(t)x^2}{2\sigma^2})}$$とおくと，

$$
\begin{align*}
\frac{x^2}{2\sigma^2}\left\{2\alpha g(t)-\frac{{\rm d} g(t)}{{\rm d}t}\right\}\tilde{f}(x,t)&=0\\
\therefore g(t)&=\exp(2\alpha t)
\end{align*}
$$

$$
\begin{align*}
\therefore f(x,t)&=\frac{1}{\sqrt{2\pi(\sigma{\rm e}^{-\alpha t})^2}}\exp\left(-\frac{1}{2(\sigma{\rm e}^{-\alpha t})^2}x^2\right)\\
&=\mathcal{N}\left(0, (\sigma{\rm e}^{-\alpha t})^2\right)
\end{align*}
$$

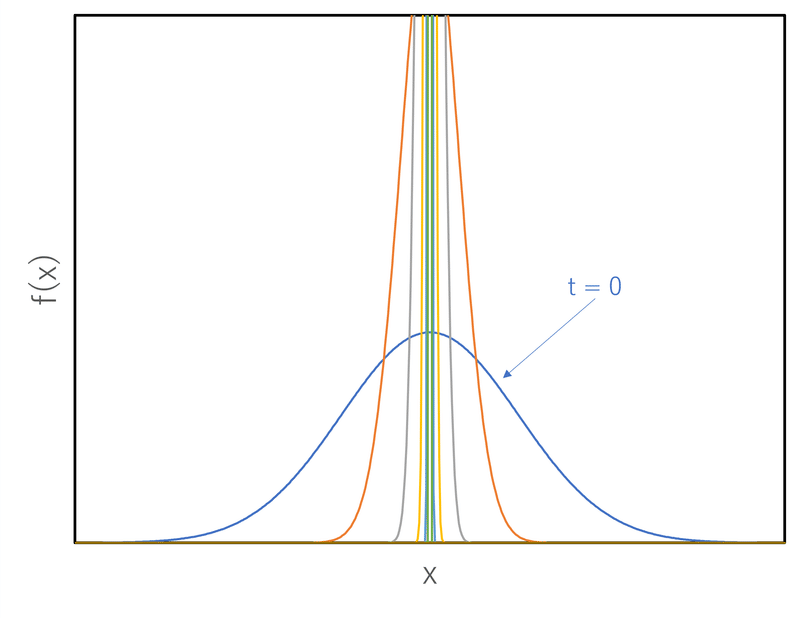
b. $${\alpha>0}$$の場合，ガウス分布の分散は指数関数的に小さくなるため，$${t\rightarrow \infty}$$で$${\delta(x)}$$に収束する。時間発展の様子を図3に示す。

図３：α > 0の場合の時間発展の様子

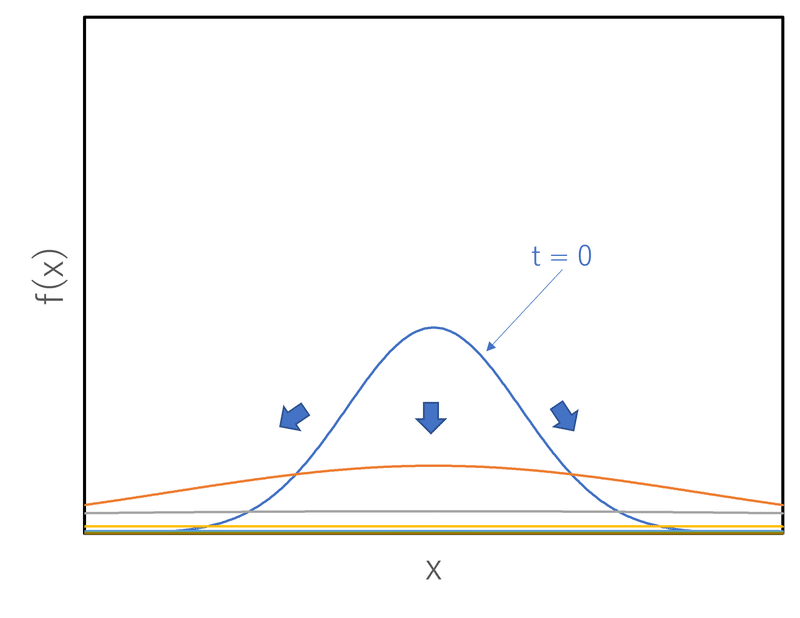
一方，$${\alpha<0}$$の場合，ガウス分布の分散は指数関数的に大きくなるため，時間発展につれて一様分布に漸近する。時間発展の様子を図4に示す。

図４：α < 0の場合の時間発展の様子

c. 

$$
\begin{align*}
\int_{-\infty}^{\infty}{\rm d}xf(x,t)&=\int_{-\infty}^{\infty}{\rm d}x\mathcal{N}\left(0, (\sigma{\rm e}^{-\alpha t})^2\right)\\
&=1
\end{align*}
$$

Problem 2.6

Gibbsは位相空間での分布関数$${f(\mathbf{x},t)}$$を用いて以下のエントロピーの表式を定義した。

$$
\begin{align*}
S(t)&=-k\int{\rm d}\mathbf{x}f(\mathbf{x},t)\ln f(\mathbf{x},t)
\end{align*}
$$

ここで，式(2.5.13)で与えられるリウヴィル方程式を満たすと仮定する。

$$
\begin{align*}
\frac{\partial}{\partial t}f(\mathbf{x},t)+\eta(\mathbf{x},t)\cdot\nabla f(\mathbf{x},t)&=0\\
\eta(\mathbf{x},t)&=\dot{\mathbf{x}}
\end{align*}\tag{2.5.13}
$$

このように定義されたエントロピーは時間の関数であることを明示するため$${S(t)}$$と表記している。

a. 任意の分布関数に対してエントロピーが定数であること，すなわち$${{\rm d}S/{\rm d}t=0,\ S(t)=S(0)}$$であり，任意のアンサンブルに対して$${S(t)}$$は増加できないことを示せ。これは熱力学第二法則の破綻を意味するか？
ヒント：積分に対する$${{\rm d}/{\rm d}t=0}$$の適用に注意せよ。

b. 分布$${f(\mathbf{x},t)}$$は微視的（fine-grained）分布関数として知られる。$${f(\mathbf{x},t)}$$は位相空間の各点で完全に定義されるため，位相空間の微細構造の詳細情報の全てを含んでいるが，現実的にはそれら詳細情報を把握する解像度を得ることはできない。そのため，以下の操作によって定義される粗視化（coarse-grained）分布$${\bar{f}(\mathbf{x},t)}$$を考えることにする：$${\bar{f}(\mathbf{x},t)}$$を定義できる最小セル$${C}$$に位相空間を分割する。各セルは更に小さい体積$${\Delta \mathbf{x}}$$を有するサブセルに分割される。サブセルの中点は$${\mathbf{x}}$$に位置し，サブセルには確率$${f(\mathbf{x},t)\Delta\mathbf{x}}$$が含まれる。$${t=0}$$では$${\bar{f}(\mathbf{x},0)=f(\mathbf{x},t)}$$であるとする。$${t>0}$$における$${\bar{f}(\mathbf{x},t)}$$を定義するため，各時間$${t}$$において，$${f>\bar{f}}$$を満たすサブセルから$${f<\bar{f}}$$を満たすサブセルへ確率を移動させることにする。粗視化エントロピーは$${\bar{f}(\mathbf{x},t)}$$を用いて

$$
\begin{align*}
\bar{S}(t)&=-k\int{\rm d}\mathbf{x}\bar{f}(\mathbf{x},t)\ln \bar{f}(\mathbf{x},t)
\end{align*}
$$

と定義される。ここで積分は，分割された位相空間のセル$${C}$$を全て足しあげることを意味する。今回の粗視化において，$${\bar{S}(t)\geq\bar{S}(0)}$$（等式は平衡状態のときのみ成立する）が成立することを示せ。
ヒント：ある１つのサブセルから他のサブセルへの確率移動に対して$${\bar{S}}$$の変化が非負であることを示せ。これは，粗視化エントロピーが時間に対して非負であることの十分条件である。

---

a.

$$
\begin{align*}
\frac{{\rm d}S(t)}{{\rm d}t}&=-k\int{\rm d}\mathbf{x}\frac{{\rm d}f(\mathbf{x},t)}{{\rm d}t}\ln f(\mathbf{x},t)-k\int{\rm d}\mathbf{x}f(\mathbf{x},t)\frac{{\rm d}\ln f(\mathbf{x},t)}{{\rm d}t}\\
&=-k\int{\rm d}\mathbf{x}\frac{{\rm d}f(\mathbf{x},t)}{{\rm d}t}\\
&=0\\
\therefore \frac{{\rm d}S(t)}{{\rm d}t}&=0
\end{align*}
$$

リウヴィル方程式を満たす分布関数は時間に対して状態数（情報量）が変化しないため，熱力学第二法則と理論的に矛盾はしていない。ただし，そのような分布関数を扱うことは現実的には不可能であり，理論上でしか存在しえない架空のモデルを取り扱っていることに相当する。

b.  $${\bar{f}(\mathbf{x},t)}$$を以下のように定義する。

$$
\begin{align*}
\bar{f}(\mathbf{x},t)&:=\sum_{\mathbf{x}_i\in \mathcal{C}}p(\mathbf{x}_i,t| \mathcal{C})f(\mathbf{x}_i,t)\\
\sum_{\mathbf{x}_i\in \mathcal{C}}p(\mathbf{x}_i,t| \mathcal{C})&=1
\end{align*}
$$

ここで，$${f(\mathbf{x}_1,t)>\bar{f}(\mathbf{x},t), f(\mathbf{x}_2,t)<\bar{f}(\mathbf{x},t)}$$となっており，$${f(\mathbf{x}_1,t)}$$の重み係数を$${f(\mathbf{x}_2,t)}$$に移動させる過程を考える。

$$
\begin{align*}
p'(\mathbf{x}_1,t| \mathcal{C})&:= p(\mathbf{x}_1,t| \mathcal{C}) - \lambda\\
 p'(\mathbf{x}_2,t| \mathcal{C})&:= p(\mathbf{x}_2,t| \mathcal{C}) + \lambda\\
0&\leq \lambda \leq p(\mathbf{x}_1,t| \mathcal{C})
\end{align*}
$$

確率を移動させた後の粗視化された分布関数を$${\bar{f}'(\mathbf{x},t)}$$とおくと，

$$
\begin{align*}
-k\bar{f}'(\mathbf{x},t)\ln\bar{f}'(\mathbf{x},t)&\geq-k\bar{f}'(\mathbf{x},t)\left(\sum_{\mathbf{x}_i\in \mathcal{C}}p(\mathbf{x}_i,t| \mathcal{C})\ln f(\mathbf{x}_i,t)-\lambda\ln f(\mathbf{x}_1,t)+\lambda\ln f(\mathbf{x}_2,t)\right)\\
&=-k\bar{f}'(\mathbf{x},t)\left(\sum_{\mathbf{x}_i\in \mathcal{C}}p(\mathbf{x}_i,t| \mathcal{C})\ln f(\mathbf{x}_i,t)\right)+k\lambda\ln\left\{\frac{ f(\mathbf{x}_1,t)}{f(\mathbf{x}_2,t)}\right\}\\
&\geq 0
\end{align*}
$$

が成立する。
以上より，今回仮定した$${\bar{S}(t)}$$の時間発展において，$${\bar{S}(t)\geq\bar{S}(0)}$$が成立する。

Problem 2.7

位相空間$${(p_x,p_y,p_z,x,y,z)}$$を用いて3次元空間を運動する単粒子の状態を考える。極座標$${(r,\theta,\phi)}$$及びその正準共役な運動量$${p_r,p_{\theta},p_{\phi}}$$への正準変換を導き，また位相空間の微小体積要素$${{\rm d}\mathbf{p}{\rm d}\mathbf{x}}$$が以下の関係式を満たすことを示せ。

$$
\begin{align*}
{\rm d}p_x{\rm d}p_y{\rm d}p_z{\rm d}x{\rm d}y{\rm d}z&={\rm d}p_r{\rm d}p_{\phi}{\rm d}p_{\theta}{\rm d}r{\rm d}\theta{\rm d}\phi
\end{align*}
$$

---

$$
\begin{align*}
x&=r\sin\theta\cos\phi\\
y&=r\sin\theta\sin\phi\\
z&=r\cos\theta\\
\end{align*}
$$

より，それらを時間微分すると，

$$
\begin{align*}
\dot{x}&=\dot{r}\sin\theta\cos\phi+r\dot{\theta}\cos\theta\cos\phi-r\dot{\phi}\sin\theta\sin\phi\\
\dot{y}&=\dot{r}\sin\theta\sin\phi+r\dot{\theta}\cos\theta\sin\phi+r\dot{\phi}\sin\theta\cos\phi\\
\dot{z}&=\dot{r}\cos\theta-r\dot{\theta}\sin\theta
\end{align*}
$$

となる。
粒子の質量を$${m}$$として運動エネルギー$${K}$$を極座標で表すと，

$$
\begin{align*}
K&=\frac{m}{2}\left(\dot{x}^2+\dot{y}^2+\dot{z}^2\right)\\
&=\frac{m}{2}\left(\dot{r}^2+r^2\dot{\theta}^2+r^2\dot{\phi}^2\sin^2\theta\right)\\
\end{align*}
$$

以上より，極座標$${(r,\theta,\phi)}$$の正準共役な運動量$${p_r,p_{\theta},p_{\phi}}$$は以下で与えられる。

$$
\begin{align*}
p_r&=\frac{\partial K}{\partial \dot{r}}\\
&=m\dot{r}\\
&=m\left(\frac{\partial r}{\partial x}\dot{x}+\frac{\partial r}{\partial y}\dot{y}+\frac{\partial r}{\partial z}\dot{z}\right)\\
&=\frac{xp_x+yp_y+zp_z}{\sqrt{x^2+y^2+z^2}}\\
p_{\theta}&=\frac{\partial K}{\partial \dot{\theta}}\\
&=mr^2\dot{\theta}\\
&=mr^2\left(\frac{\partial \theta}{\partial x}\dot{x}+\frac{\partial \theta}{\partial y}\dot{y}+\frac{\partial \theta}{\partial z}\dot{z}\right)\\
&=\frac{zxp_x+xyp_y+(x^2+y^2)p_z}{\sqrt{x^2+y^2}}\\
p_{\phi}&=\frac{\partial K}{\partial \dot{\phi}}\\
&=mr^2\sin^2\theta\dot{\phi}\\
&=mr^2\sin^2\theta\left(\frac{\partial \phi}{\partial x}\dot{x}+\frac{\partial \phi}{\partial y}\dot{y}\right)\\
&=\frac{-yp_x+xp_y}{x^2}\\
\end{align*}
$$

次に正準変換に対応するヤコビアンを計算する。

$$
\begin{align*}
\frac{\partial x}{\partial r}&=\sin\theta\cos\phi,&\frac{\partial x}{\partial \theta}&=r\cos\theta\cos\phi,&\frac{\partial x}{\partial \phi}&=-r\sin\theta\sin\phi\\
\frac{\partial x}{\partial p_r}&=0,&\frac{\partial x}{\partial p_{\theta}}&=0,&\frac{\partial x}{\partial p_{\phi}}&=0\\
\frac{\partial y}{\partial r}&=\sin\theta\sin\phi,&\frac{\partial y}{\partial \theta}&=r\cos\theta\sin\phi,&\frac{\partial y}{\partial \phi}&=r\sin\theta\cos\phi\\
\frac{\partial y}{\partial p_r}&=0,&\frac{\partial y}{\partial p_{\theta}}&=0,&\frac{\partial y}{\partial p_{\phi}}&=0\\
\frac{\partial z}{\partial r}&=\cos\theta,&\frac{\partial z}{\partial \theta}&=-r\sin\theta,&\frac{\partial z}{\partial \phi}&=0\\
\frac{\partial z}{\partial p_r}&=0,&\frac{\partial z}{\partial p_{\theta}}&=0,&\frac{\partial z}{\partial p_{\phi}}&=0\\
\frac{\partial p_x}{\partial p_r}&=\sin\theta\cos\phi,&\frac{\partial p_x}{\partial p_{\theta}}&=\frac{\cos\theta\cos\phi}{r},&\frac{\partial p_x}{\partial p_{\phi}}&=-\frac{\sin\phi}{r\sin\theta}\\
\frac{\partial p_y}{\partial p_r}&=\sin\theta\sin\phi,&\frac{\partial p_x}{\partial p_{\theta}}&=\frac{\cos\theta\sin\phi}{r},&\frac{\partial p_x}{\partial p_{\phi}}&=\frac{\cos\phi}{r\sin\theta}\\
\frac{\partial p_z}{\partial p_r}&=\cos\theta,&\frac{\partial p_x}{\partial p_{\theta}}&=-\frac{\sin\theta}{r},&\frac{\partial p_z}{\partial p_{\phi}}&=0\\
\end{align*}
$$

より，

$$
\begin{align*}
\frac{\partial(x,y,z,p_x,p_y,p_z)}{\partial(r,\theta,\phi,p_{r},p_{\theta},p_{\phi})}&=\begin{Vmatrix}
\sin\theta\cos\phi&r\cos\theta\cos\phi&-r\sin\theta\sin\phi&0&0&0\\
\sin\theta\sin\phi&r\cos\theta\sin\phi&r\sin\theta\cos\phi&0&0&0\\
\cos\theta&-r\sin\theta&0&0&0&0\\
\frac{\partial p_x}{\partial r}&\frac{\partial p_x}{\partial \theta}&\frac{\partial p_x}{\partial \phi}&\sin\theta\cos\phi&\frac{\cos\theta\cos\phi}{r}&-\frac{\sin\phi}{r\sin\theta}\\
\frac{\partial p_y}{\partial r}&\frac{\partial p_y}{\partial \theta}&\frac{\partial p_y}{\partial \phi}&\sin\theta\sin\phi&\frac{\cos\theta\sin\phi}{r}&\frac{\cos\phi}{r\sin\theta}\\
\frac{\partial p_z}{\partial r}&\frac{\partial p_z}{\partial \theta}&0&\cos\theta&-\frac{\sin\theta}{r}&0\\
\end{Vmatrix}\\
&=\begin{Vmatrix}
0&0&-r\frac{\sin\theta}{\sin\phi}&0&0&0\\
\sin\theta\sin\phi&r\cos\theta\sin\phi&r\sin\theta\cos\phi&0&0&0\\
\cos\theta&-r\sin\theta&0&0&0&0\\
\frac{\partial p_x}{\partial r}&\frac{\partial p_x}{\partial \theta}&\frac{\partial p_x}{\partial \phi}&\sin\theta\cos\phi&\frac{\cos\theta\cos\phi}{r}&-\frac{\sin\phi}{r\sin\theta}\\
\frac{\partial p_y}{\partial r}&\frac{\partial p_y}{\partial \theta}&\frac{\partial p_y}{\partial \phi}&\sin\theta\sin\phi&\frac{\cos\theta\sin\phi}{r}&\frac{\cos\phi}{r\sin\theta}\\
\frac{\partial p_z}{\partial r}&\frac{\partial p_z}{\partial \theta}&0&\cos\theta&-\frac{\sin\theta}{r}&0\\
\end{Vmatrix}\\
&=\frac{-r\sin\theta}{\sin\phi}\begin{Vmatrix}
\sin\theta\sin\phi&r\cos\theta\sin\phi&0&0&0\\
\cos\theta&-r\sin\theta&0&0&0\\
\frac{\partial p_x}{\partial r}&\frac{\partial p_x}{\partial \theta}&\sin\theta\cos\phi&\frac{\cos\theta\cos\phi}{r}&-\frac{\sin\phi}{r\sin\theta}\\
\frac{\partial p_y}{\partial r}&\frac{\partial p_y}{\partial \theta}&\sin\theta\sin\phi&\frac{\cos\theta\sin\phi}{r}&\frac{\cos\phi}{r\sin\theta}\\
\frac{\partial p_z}{\partial r}&\frac{\partial p_z}{\partial \theta}&\cos\theta&-\frac{\sin\theta}{r}&0\\
\end{Vmatrix}\\
&=\frac{-r\sin\theta}{\sin\phi}\begin{Vmatrix}
0&r\frac{\sin\phi}{\cos\theta}&0&0&0\\
\cos\theta&-r\sin\theta&0&0&0\\
\frac{\partial p_x}{\partial r}&\frac{\partial p_x}{\partial \theta}&\sin\theta\cos\phi&\frac{\cos\theta\cos\phi}{r}&-\frac{\sin\phi}{r\sin\theta}\\
\frac{\partial p_y}{\partial r}&\frac{\partial p_y}{\partial \theta}&\sin\theta\sin\phi&\frac{\cos\theta\sin\phi}{r}&\frac{\cos\phi}{r\sin\theta}\\
\frac{\partial p_z}{\partial r}&\frac{\partial p_z}{\partial \theta}&\cos\theta&-\frac{\sin\theta}{r}&0\\
\end{Vmatrix}\\
&=\frac{r^2\sin\theta}{\cos\theta}\begin{Vmatrix}
\cos\theta&0&0&0\\
\frac{\partial p_x}{\partial r}&\sin\theta\cos\phi&\frac{\cos\theta\cos\phi}{r}&-\frac{\sin\phi}{r\sin\theta}\\
\frac{\partial p_y}{\partial r}&\sin\theta\sin\phi&\frac{\cos\theta\sin\phi}{r}&\frac{\cos\phi}{r\sin\theta}\\
\frac{\partial p_z}{\partial r}&\cos\theta&-\frac{\sin\theta}{r}&0\\
\end{Vmatrix}\\
&=r^2\sin\theta\begin{Vmatrix}
\sin\theta\cos\phi&\frac{\cos\theta\cos\phi}{r}&-\frac{\sin\phi}{r\sin\theta}\\
\sin\theta\sin\phi&\frac{\cos\theta\sin\phi}{r}&\frac{\cos\phi}{r\sin\theta}\\
\cos\theta&-\frac{\sin\theta}{r}&0\\
\end{Vmatrix}\\
&=r^2\sin\theta\left\{\frac{1}{r^2}\left(\sin\theta+\frac{\cos\theta}{\sin\theta}\right)\right\}\\
&=\sin^2\theta+\cos^2\theta\\
&=1\\
\therefore {\rm d}p_x{\rm d}p_y{\rm d}p_z{\rm d}x{\rm d}y{\rm d}z&=\frac{\partial(x,y,z,p_x,p_y,p_z)}{\partial(r,\theta,\phi,p_{r},p_{\theta},p_{\phi})}{\rm d}p_r{\rm d}p_{\phi}{\rm d}p_{\theta}{\rm d}r{\rm d}\theta{\rm d}\phi\\
&={\rm d}p_r{\rm d}p_{\phi}{\rm d}p_{\theta}{\rm d}r{\rm d}\theta{\rm d}\phi
\end{align*}
$$

参考文献

• Mark Tuckerman, Statistical Mechanics: Theory and Molecular Simulation (Oxford Graduate Texts)