ノーベル平和賞の計算note①

大学生になったら始めることといえばアルバイトだろう。アルバイトが禁止の高校も多いだろうし、禁止でなくとも学生の過半数がバイトをしているという高校も少ないだろう。というわけで私も大学生のご多分に漏れず細々と塾講師アルバイトをしており、専門でもない英語や数学の授業をしている。普段使わないような脳の領域を使うことで頭の体操をしている感覚を得ているからだろうか、個人的には英語よりも数学の授業をしている方が好きだ。さて、最近バイト先で面白い問題を解く機会があったので備忘録代わりに載せておく。数学に覚えのある方はぜひ挑戦してみて欲しい。タイトルは計算note①と称したが②が出るかどうかは分からない。

図1

問題：図1のような△ABCについて、点D,E,FはそれぞれBC,CA,AB上の点であり、DEとABの交点をX、CAとFDの交点をY、BCとEFの交点をZとする。このとき3点X,Y,Zが一直線上にあることを証明せよ。ただし、AD,BE,CFは△ABCの内心を通っており、また△ABCは二等辺三角形ではないものとする。

文系大学生にはかなり荷が重い問題だ。方針を立てるのにも一苦労するのではないだろうか？受け持ちの生徒たちが黙々とテスト勉強をする傍ら、私も生徒のテスト範囲と照らし合わせて発狂しながらペンを走らせていた。以下に私の思考を載せておくので、自力で解きたいという方はここで一度スクロールするのをとめると良いだろう。余談だが、当然このような平面図形をデジタルで描くのは初めてだったので大苦戦を強いられた。なんか図形歪んでない？というのはご愛嬌ということで一つ手をうってもらいたい。

まずは解答の方針だがメネラウスの定理の逆を使って証明を進める。メタい話だが問題を持ち込んだ生徒の試験範囲が数学Aの一部であったため、この方針自体はすぐに立てることが出来た。全くの自力でメネラウスの定理の逆に行き着いた方はおそらく相当数学に覚えがある方ばかりだろう。

メネラウスの定理？逆とは？という方のために詳しく解説を載せておく。知ってるよという方は図4のところまで飛ばしてほしい。

メネラウスの定理とその逆とは下記のような定理である。

図2

メネラウスの定理
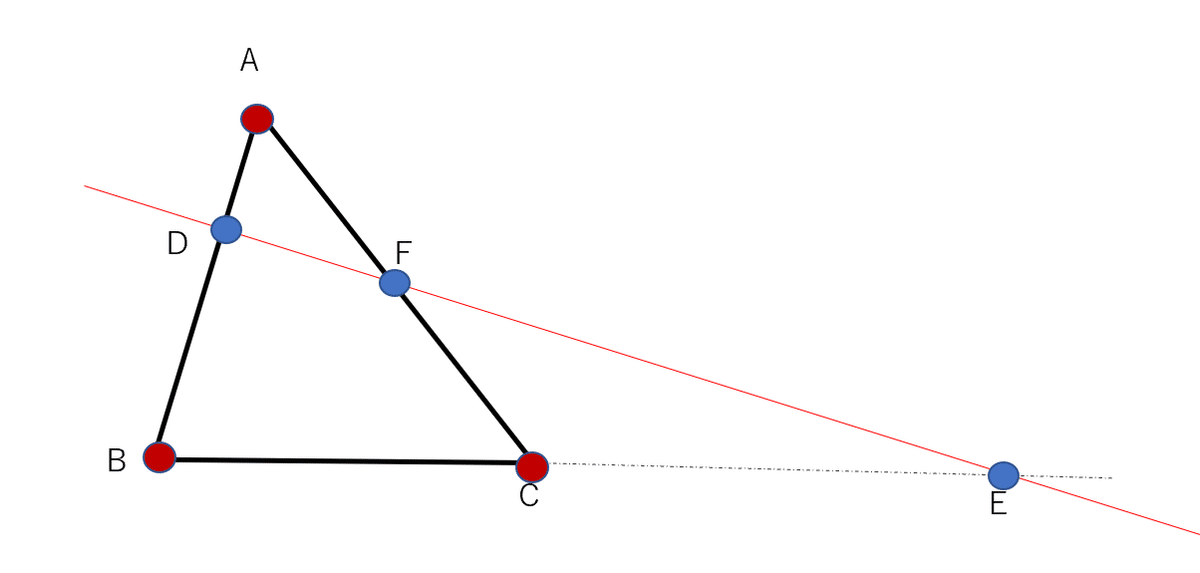
一つの直線が三角形の各辺またはその延長線と交わるとき、(図2で言えば赤い直線と三角形ABC)、三角形の辺を内分または外分する比の値の間には、次の等式が成り立つ。

$$
\frac{AD}{DB}×\frac{BE}{EC}×\frac{CF}{FA}=1
$$

「公式、、、覚える、、、うぅ、頭が……」という人は、図2で赤丸で示した三角形の頂点と青丸で示した辺の分点を頂点Aから「頂点(赤)→分点(青)→頂点(赤)→分点(青)…」といった具合に指で追いかけてみると分かりやすいだろう。

メネラウスの定理の逆
図2のように△ABCの辺AB,BC,CAまたはその延長上にそれぞれ点D,E,Fがあるとき、

$$
\frac{AD}{DB}×\frac{BE}{EC}×\frac{CF}{FA}=1
$$

を満たすならば、三点D,E,Fは一直線上にある。

今回の問題のように3点が一直線上に存在することを証明するためには、メネラウスの定理の逆を用いて、
「メネラウスの定理の等式が成立するため、メネラウスの定理の逆より3点X,Y,Zは一直線上に存在する」といった証明方針になるわけだ。
「しかし、ちょっと待てよと、今回の図1でどうやってメネラウスの定理を適用するんだ？」と思った方も多いだろう。確かに明らかに見慣れた形とは違うが果たしてどうなのか？

なぜ見慣れた形ではないのかというと、今回の問題はメネラウスの定理の拡張を用いた問題だからである。かく言う私も中学・高校で習った覚えがない(忘れているだけかもしれないが…)のだが、そこまで難しい話ではない。メネラウスの定理の拡張とは下記のとおりである。

図３

メネラウスの定理の拡張
一つの直線が三角形の各辺の延長線と交わるとき、(図3で言えば赤い直線と三角形ABC)、三角形の辺を外分する比の値の間には、次の等式が成り立つ。

$$
\frac{AD}{DB}×\frac{BE}{EC}×\frac{CF}{FA}=1
$$

定理の等式は全く同じだし、定理の文言も一般的なメネラウスの定理をほぼコピペした。図2と図3で何が違うのかと言えば、赤い直線が△ABCの内部を通っているか、外部を通っているかである。そして、メネラウスの定理は拡張の場合でも逆は成立するので、今回の問題では拡張したメネラウスの定理の逆を適用することになる。

メネラウスの定理のまとめ
同一平面上にある直線は平行でない限り必ず一点で交わる。したがって、三角形の辺と平行ではない直線が三角形の内部を通っていれば内分点2つと外分点1つが、三角形の外部を通っていれば外分点3つが出来上がる。このようにして作られた分点と三角形の頂点を結ぶ線分の比についての定理がメネラウスの定理となるわけだ。

図4

さて本題に戻る。まずは図4を見ながら示すべきメネラウスの等式を考えよう。ABの延長線上にX、BCの延長線上にZ、CAの延長線上にYがあることを確認して、AX→XB→BZ→ZC→CY→YAと進むと「頂点(赤)→分点(青)→頂点(赤)→分点(青)…」の順に一周できる。したがって示すべき等式は

$$
\frac{AX}{XB}×\frac{BZ}{ZC}×\frac{CY}{YA}=1　
$$

となるわけだ。この等式(＊)が必ず成立することを示せば晴れて証明終了となる。今回の問題は辺の長さに関する具体的な情報は何一つないので、(＊)を示すためにもメネラウスの定理を用いる。(＊)でかけられている3つの項は一般的なメネラウスの定理にも登場することに気づいた方は多いだろう。例えば一番最初の項は△ABCでメネラウスの定理を用いたときの

$$
\frac{AX}{XB}×\frac{BD}{DC}×\frac{CE}{EA}=1　
$$

にも登場する。「図形が複雑でどこに注目すればいいかわからないが（#^ω^）」という方も落ち着いてほしい。

図５

結局メネラウスの定理で使う分点は一直線上にあるわけだから、Xが分点であると見た以上、図5の青丸のようにしか分点は配置されえない。したがって、分点D,Eを巻き込むようにメネラウスの定理の等式を立てることが出来るのだ。

図6

図6のように見て、分点F,Eを巻き込んで式を立てると

$$
\frac{BZ}{ZC}×\frac{CE}{EA}×\frac{AF}{FB}=1　
$$

が成立し、

図7

図7のように見て、分点F,Dを巻き込んで式を立てると

$$
\frac{CY}{YA}×\frac{AF}{FB}×\frac{BD}{DC}=1　
$$

が成立するのだ。

さて、ここまでくればもう一歩。図5~図7を見ながら立てた三つの等式の左辺と右辺を全てかけると以下のようになる。

$$
\frac{AX}{XB}×\frac{BD}{DC}×\frac{CE}{EA}×\frac{BZ}{ZC}×\frac{CE}{EA}×\frac{AF}{FB}×\frac{CY}{YA}×\frac{AF}{FB}×\frac{BD}{DC}=1
$$

これを少し並び替えて整理すると

$$
\frac{AX}{XB}×\frac{BZ}{ZC}×\frac{CY}{YA}×\frac{BD}{DC}×\frac{CE}{EA}×\frac{AF}{FB}× \frac{BD}{DC}×\frac{CE}{EA}×\frac{AF}{FB}=1
$$

となる。この等式を(＊＊)とする。

お気づきの方も多いだろう。そう、メネラウスの定理の相方ことチェバの定理の出番である。チェバの定理より

$$
\frac{BD}{DC}×\frac{CE}{EA}×\frac{AF}{FB}=1
$$

が成立するため、(＊＊)の等式は、

$$
\frac{AX}{XB}×\frac{BZ}{ZC}×\frac{CY}{YA}×1×1=1
$$

$$
\frac{AX}{XB}×\frac{BZ}{ZC}×\frac{CY}{YA}=1
$$

となり、(＊)の式が示された。
したがって、メネラウスの定理の逆よりX,Y,Zは一直線上に存在する。
(証明終ry

終了できません。残念だったな！
いやぁ困ったことになったねぇ。
なぜ私が困っているのか、勘の良い方はもうお気づきだろう。問題文をもう一度よく読みかえそう。

問題：図1のような△ABCについて、点D,E,FはそれぞれBC,CA,AB上の点であり、DEとABの交点をX、CAとFDの交点をY、BCとEFの交点をZとする。このとき3点X,Y,Zが一直線上にあることを証明せよ。ただし、AD,BE,CFは△ABCの内心を通っており、また△ABCは二等辺三角形ではないものとする。

内心と二等辺三角形ではないという話はどこへ行った…？
意気揚々と答案を書き上げた私は途方に暮れてしまった。生徒から突き刺さる「え、先生こんなのも分からないんですか？数弱なんですか？」という視線、は別になかったが、問題文に書かれていることは問題を解くために必須の条件であると見てよい。よく見返してみたが、ここまで書いた答案におそらく不備はない。なぜなのか…

この謎に一瞬で気が付いた人は相当に数学のできる人だろう。かく言う私はこれに気づくのに短くない時間を要した。そのヒントは、この記事の中にすでに仕込んであるのだがお気づきになった人はいるだろうか。

もう一度メネラウスの定理のまとめを見てみよう。

メネラウスの定理のまとめ
同一平面上にある直線は平行でない限り必ず一点で交わる。したがって、三角形の辺と平行ではない直線が三角形の内部を通っていれば内分点2つと外分点1つが、三角形の外部を通っていれば外分点3つが出来上がる。このようにして作られた分点と三角形の頂点を結ぶ線分の比についての定理がメネラウスの定理となるわけだ。

図1

太字部分を踏まえてもう一度、図1を見てみよう。生徒の持っていた問題用紙には最初からこの図が描かれていたわけだが、例えばABとDEは絶対に平行ではないといえるのだろうか？もし平行だったら点X存在しないけど大丈夫ソ？
といったように、正直小馬鹿にされたような気分だったが、どうやら問題文後半の但し書きは三点X,Y,Zの存在を約束するための条件のようだ。これに言及しないと減点は免れない……かどうかは少し微妙である。先ほども言ったように図がすでに問題用紙に描かれていたので、出題の時点でX,Y,Zの存在を前提として出題されていることもありうる。ようするに、三点X,Y,Zの存在についての証明の有無は問われていない可能性もあるわけだ。

とはいえ一応これについても考えておこう。こちらはさほど難しくはない。結局ABとDEが平行でなければ、点Xの存在は約束される。というわけでこのことを示すためには

$$
CE:EA\ne CD:DB
$$

であることを示せばよい。
AD,BE,CFは内心を通っているから、各線分は内角の二等分線である。したがって角の二等分線の定理より

$$
CE:EA=BC:AB
$$

$$
CD:DB=CA:AB
$$

この二つの比例式の右辺を見る。△ABCは二等辺三角形ではないので、同じ長さの辺は存在しない、したがって

$$
BC\ne CA
$$

より

$$
BC:AB\ne CA:AB
$$

したがって、

$$
CE:EA\ne CD:DB
$$

であることが分かったので、

$$
AB\nparallel DE
$$

となり、ABとDEの交点となるXは確かに存在する。
同様にして

$$
CA\nparallel FD
$$

$$
BC\nparallel EF
$$

であることも分かるので、Y,Zも確かに存在する。

これらのことを証明することによって初めて図5～図7のようにメネラウスの定理を使うことができるのだが、この内容が解答に求められていたかどうかは不明である。なぜなら解いた後に生徒に模範解答を見せてもらったのだが、普通に角の二等分線の定理を使いながらメネラウスの等式を証明していたからだ。ざっとしか見ていないのでここに再現できないのだが、私が変な解き方をしたばかりにこんな面倒な作業をしなければいけなかったようだ。この世は理不尽である。

とはいえ久しぶりに頭を使う問題に出会うこととなった。解いた感想としては、一見相当難しそうに見えるが、メネラウスの定理の本質(三角形の辺と直線によってできる分点の関係)を理解していれば、答えにたどり着ける良問なような気がした。中学・高校のときにもう少しこういったことに目を向けていれば、数学への意識も変わっていたのだろうか？

最後に解答の清書をまとめておくが、ほとんど上記のコピペなので新しい情報はない。ここまでお付き合いいただき感謝する。積極的に数学に関わっているわけではないので、面白い問題とかを教えてくださると5%くらいの確率でnoteにするかもしれません。
それではまた…

(証明)
点X,Y,ZはAB,CA,BCの外分点であるため、

$$
\frac{AX}{XB}×\frac{BZ}{ZC}×\frac{CY}{YA}=1　
$$

の等式(＊)が成立すれば、メネラウスの定理の逆より△ABCの各辺の外分点であるX,Y,Zは一直線上に存在する。
ここで△ABCでメネラウスの定理を用いると下記の3つの等式が成立する。

$$
\frac{AX}{XB}×\frac{BD}{DC}×\frac{CE}{EA}=1　
$$

$$
\frac{BZ}{ZC}×\frac{CE}{EA}×\frac{AF}{FB}=1　
$$

$$
\frac{CY}{YA}×\frac{AF}{FB}×\frac{BD}{DC}=1　
$$

ただし、AD,BE,CFは内心を通っているから、各線分は内角の二等分線である。したがって角の二等分線の定理より

$$
CE:EA=BC:AB
$$

$$
CD:DB=CA:AB
$$

この二つの比例式の右辺を見る。△ABCは二等辺三角形ではないので、同じ長さの辺は存在しない、したがって

$$
BC\ne CA
$$

より

$$
BC:AB\ne CA:AB
$$

したがって

$$
CE:EA\ne CD:DB
$$

であることがわかったので

$$
AB\nparallel DE
$$

となり、ABとDEは必ず一点で交わるため、Xは確かに存在する。
同様にして

$$
CA\nparallel FD
$$

$$
BC\nparallel EF
$$

であることも分かるので、Y,Zも確かに存在し、上記の3つの等式の成立は約束される。
この3つの等式の左辺と右辺をそれぞれかけて整理すると、

$$
\frac{AX}{XB}×\frac{BD}{DC}×\frac{CE}{EA}×\frac{BZ}{ZC}×\frac{CE}{EA}×\frac{AF}{FB}×\frac{CY}{YA}×\frac{AF}{FB}×\frac{BD}{DC}=1
$$

$$
\frac{AX}{XB}×\frac{BZ}{ZC}×\frac{CY}{YA}×\frac{BD}{DC}×\frac{CE}{EA}×\frac{AF}{FB}× \frac{BD}{DC}×\frac{CE}{EA}×\frac{AF}{FB} =1
$$

となる。この等式を(＊＊)とする。
ここで△ABCでチェバの定理より

$$
\frac{BD}{DC}×\frac{CE}{EA}×\frac{AF}{FB}=1
$$

の等式が成立するため、等式(＊＊)は

$$
\frac{AX}{XB}×\frac{BZ}{ZC}×\frac{CY}{YA}×1×1=1
$$

$$
\frac{AX}{XB}×\frac{BZ}{ZC}×\frac{CY}{YA}=1
$$

と変形でき、等式(＊)の成立が示された。
したがってメネラウスの定理の逆より△ABCの各辺の外分点であるX,Y,Zは一直線上に存在する。(証明終了)