分数の割り算の説明は難しい。

なぜ難しいのかというと、割り算というのは考え方が2つあり、答えの数字が同じだとしても、意味が異なるので、分かりづらいのだ。例えば、　6÷2　という簡単な割り算を考えてみる。答えはもちろん　3　である。けれど、この　3　が曲者なのだ。その理由を解説していく。

仮に（割られる数）÷（割る数）とした場合を考える。

割り算をする目的としては、（割られる数）の中に（割る数）がいくつ入っているのかを考えたり、（割られる数）を（割る数）等分した一つ分はいくつなのかを考えるといったことがある。

6÷2　の場合であれば、6の中に2が3つ入っている。6を2等分した一つ分は3である。といった具合だ。

どちらも答えは３であるが、頭の中の考え方で違いが出てくる。つまり、同じことを言っていたとしても、頭の中の考え方が違うので、ごちゃごちゃになることが多い。小学生の時にこれがごっちゃになってしまうと、算数が途端に嫌いになってしまうので、ここは気を付けたいところだ。

そして、さらにややこしいのが、割り算を掛け算の式に直すときは、再び計算式が同じであるということだ。どちらも、2×3＝6　である。2が3つあるのと、3が2つあるのだ。小学校の頃、これを図にして考えるとき、図が違うのに計算式が同じになることに違和感を感じてしまうので、わざわざ（掛ける数）と（掛けられる数）という教え方をしてしまう（この考え方は日本語の受け身などの勉強を兼ねている）のでややこしい話になってしまう。数学は答えを導く考え方が何通りもあるものなので、どちらでもいいのだ。6が知りたいので、6が出ればいいというシンプルな答えでいい。

さて、問題はこれが分数になった場合である。

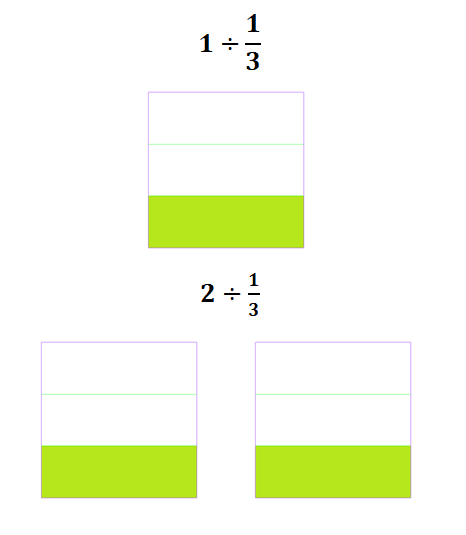
緑の部分が3分の1であることはわかると思う。さて、÷（3分の1）とは何なのかを考えていこう。この場合、1の中に（3分の1）がいくつ入っているのかを考えるとわかりやすい。図を見てみると、1の中には（3分の1）が3つ分あるので、答えは3である。下の場合も同じだ。2の中に（3分の1）はいくつあるのか。6つあるので、答えは６である。

これを考えていこう。

『いくつあるかという世界。』

この〇〇の中に◆◆はいくつあるのかというのはどういうふうに考えているのかを考えていこうと思う。

まず初めに、物の数を数えるときは、1つ2つ3つと、１つずつ数えていると思う。これが、１つずつではなく、◆◆ずつ数える世界に変わるわけだ。

例えば、10（10かどうかは数えてみるまで分からない）数えるときは、1つずつ数えて、数え切ったときにいくつ数えたのかを考えているわけだ。この場合、数え切ったときに10回数えたので、10あったことがわかるわけだ。

これが（3分の1）だとどうなるのかというと、（3分の1）を基準に、（3分の1）ずつ数えていくので、上の式だと、（3分の1）（3分の2）（3分の3＝１）と1まで数えたとき、3回数えたので、答えは　３　になる。同様に、下の場合も考えると、（3分の1）（3分の2）（3分の3=1）（3分の4）（3分の5）（3分の6=2）で、6回数えたので、答えは　６　になるというわけ。

疑問に思わず当たり前にやっていることを、「なぜ？」と思い考えてみると、意外と物事が分かったりするときがあるので、疑問に思うのはオススメだ。

さて、もっと簡単に分かる方法はないのかというのが考えどころだ。

「逆数を掛ければいい。」ということの説明。

分数の入っている式を、分数のない形にしてみるとわかるかもしれない。

書き換えると、　1÷（1÷3）というふうになる。（）は『でんこうせっか』で優先順位が高いので、（）を先に文章に直しつつ考えてみるとこうなる。

1を3つに分けたもの（1÷3）は、1の中にいくつ入っているか。

1を3つに分けたのだから、3つあるよね。説明終了だ。次に　2÷（1÷3）のときも同様に考えると、1を3つに分けたものは、２の中にいくつ入っているか。

1の中に3つあり、それが2つあるので、2×3＝6　になるよね、ということ。つまり、これが逆数を掛けるということに繋がる。

÷（1÷3）というのは ×3 と同じことなんだということが分かった。

これで、逆数にして計算するということができるようになったわけだ。この考え方は、のちのちすごく出てくるので、小学生のうちに覚えることができれば、高校生までの数学は余裕である。

ここを考えずに、「なるものはなる！」で進んでしまうのでよく詰まるわけだ。「なるものはなる！」というのは、大学生になってから使おう！