
EMaT(工学系数学統一試験)勉強方法!
この記事を見る人↓
EMaTの勉強法が分からない人
EMaTの温度感が知りたい人
こんにちは。山大生です。
自分がEMaTを受ける際に、「よし、どうやって勉強したらいいのかな、、、」ってネットで調べても何も出てこなかったので、自分なりに記事にしてみました。
皆さんのお役に立てれば幸いです!
(時間のない方は、目次で見たいとこへ飛んでください!)
EMaTとは
概要はざっとこんな感じ。
以下は2023年度のものなので情報が異なる場合があります。
必ずEMaTホームページ等で確認してください!
受付期間:10月
試験日:毎年12月の第2土曜日
試験時間:13時10分~16時10分(4科目全て受けた場合)
※途中退室あり
会場:大学の講義室
試験はすべてマーク式!
受験者入室:12時30分~13時10分
受験分野数:開始時間~終了時間
2分野:13時30分~14時50分
3分野:13時30分~15時30分
4分野:13時30分~16時10分
分野は「微分積分」「線形代数」「常微分方程式」「確率・統計」の4つです。
EMaTを受けるメリット
もちろん賞を頂けるメリットもありますが、山口大学の院試の際に数学の点数としても使えます。
広島大学では、推薦入試、学部3年次生特別選抜にも使われるようです。
解いてみた
筆者の成績
興味ないかもですが、自分の得点はこちらです。
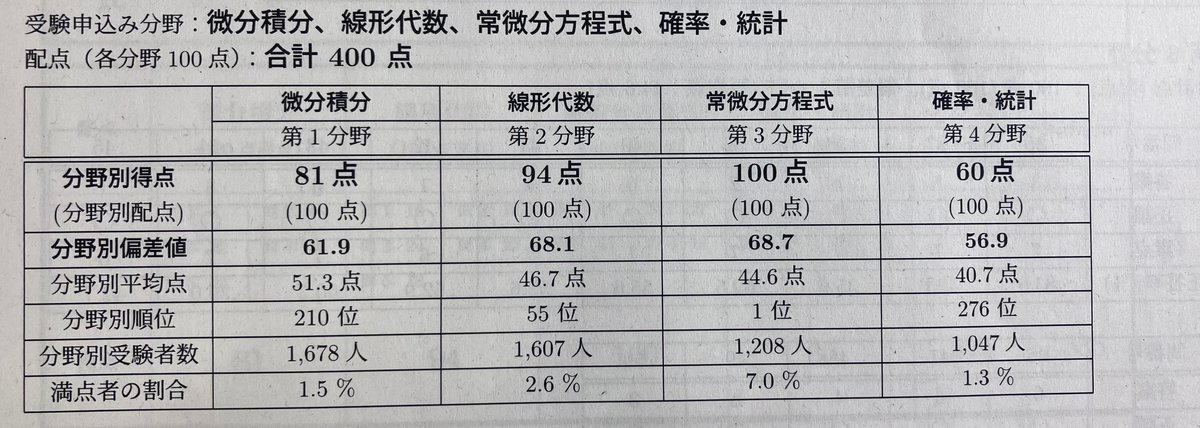
合計得点が8割(320点)を超えると学部長から優秀賞がもらえます。ついでに図書カード3000円ももらえます。
特定の分野で好成績を収めても賞がもらえるみたいです。
また、前回受けた結果よりかなり高い成績を取っても賞がもらえるみたいです。すみませんが詳しいことはわかりません。
所感
正直、普段の授業をまじめに受けていれば(ここ大事)短期間でもきちんと対策すると8割は越えられるなと思いました。
中間試験やTOEICと時期が被っているのがきついですね。
点数を見たらわかると思うのですが、時間が無さ過ぎて確率統計はちょっと捨てました。
筆者の場合の勉強スケジュール
実際に自分がしたことは以下の通りです。
11月の1か月間、テスト勉強と並行しながらEMaT勉強
1週間ごとに各分野の対策(4年分解く、見直し、復習)
EMaT前日に苦手なところの再確認・解きなおし
さらに、週3のバイトと、TOEICの受験、毎日授業にも真面目に出ていたので今思うと凄いことをしていたのかもしれません。
最後の1週間に「確率統計」の勉強をしていたのですが、テスト対策に時間を追われ(確率を勉強する気にならなかったのは秘密)基本的な部分しかできなかったです。
後悔としては、10月から地道に勉強していれば楽だったなと。
対策方法
基本的に過去問問いときゃどうにかなります。
もちろん解きっぱなしはいけませんが。
点数が取れやすい分野
常微分方程式、線形代数、微分積分、確率統計の順番に点数が取れやすいと思います。常微分方程式が一番簡単です。
満点者の割合もこの順番に多いです。
時間がない方は、捨て問を作るのもありです。
取れるところで確実に取りましょう。
1 過去問を入手
まず、大学の事務室等にEMaTの過去問題集(4年分)が置いてあるので、それを入手するか、以下のサイトから過去問を入手してください。
点数を取りたいなら4年分は解きましょう。
2 実際に解いてみる
おそらく最初は全然解けないと思いますが、頑張って解こうとしてください。(初めから答えを見ながら解かないでという意味です)
解いたら必ず分からなかった部分を復習してください。
関連しているところを教科書で復習しておこう、、とかそんなことは言いません。間違った部分が解けるようになればそれでいいです。そこまでしなくても8割取れると思います。
3 傾向と対策
過去問を4年分解けば、各分野傾向があることが分かると思います。
よく出るなと感じた部分をそれぞれの分野でまとめてみました。
微分積分
問1:極限を求める問題では、
ロピタルの定理、lim[x->±0](sinx/x)=1 が出やすいです。
微分積分では、問1が一番難しいと思います。
本番で解けないなと思ったらすぐ次に進むことをお勧めします。
また、問2~5では、ヤコビアン、極値、2変数関数などが出ます。
4年分の問題が自分の力で解けるようになっておけば基本的には大丈夫ですが、たまに思考力が問われます。誘導もあるので、誘導にうまく乗れるように練習しておきましょう。
線形代数
行列式の計算、一次独立・従属、次元、線形写像、ベクトルのなす角を使った計算等が出ます。考えて解く問題もありますが、基本的にどの年も似たようなことを問われています。
逆行列A^−1の(1,2)成分を求めよみたいな問題も頻出です。
実際に逆行列を行列から求めてもいいですが、時間がかかるので公式丸暗記でもいいから押さえておきましょう。
分からなさすぎる人は教科書などを使って丁寧に勉強してもいいかもしれません。(もちろん出た分野、自分が問題を解いていて何を言っているか分からなかった部分だけの勉強でOKです。全部復習しようとしたらきつい上に効率悪いです)
常微分方程式
この分野が一番点数取りやすいのでこの分野だけでも頑張りましょう。
いきなり例題ですが、このような問題がスラスラ解けるなら楽勝です。
(多分勉強していないと無理だと思います)
例題:y''+2y'-8y=4x-3 を解け(答えは下)
(y=○○の形にしてねって意味)
未定係数法、、、山大生なら常微分方程式の授業で習いましたが覚えていましたか?
覚えていないようでしたら下のサイトなどを参考に定着させてください。
ちなみに例題の答えは、
y=(1/4)-(1/2)x+Ce^(2x)+C'e^(-4x) (C,C':任意定数)
です。
確率・統計
出るものは決まっています(n回目)。
平均、分散、ポアソン分布、確率密度関数、条件付き確率、、、
自分自身がきちんと対策できていなかったので、大したことは言えません。ごめんなさい。
簡単な問題で落とさないこと、これだけです。
さいごに
皆さんの力になれたかは分かりませんが、
ハート押してもらえると嬉しいです。
見てくださりありがとうございました!
この記事が気に入ったらサポートをしてみませんか?
