FM音源のモジュレータ共有が残念な音色になる理由を簡単な数学で説明する
ヤマハの名器DX7に代表されるFM音源に搭載されている「アルゴリズム」(解法が無い時点でアルゴリズムと呼べないと思うのでカッコ書きにしてある)には様々なものがある。この「アルゴリズム」には問題点がいくつかある。並び順に規則性が全くなく、1番のアルゴリズムが妙に使いづらいなど、配置に検討の余地がある。オペレータのスワップができないので、音を作り替える手間がかかるのもかなり面倒だ。さらに言えば、いきなり6オペレータという選択肢を見せられるので、ユーザーは困惑するし、余計なオペレータを使用することで音色を台無しにすることもあっただろう。
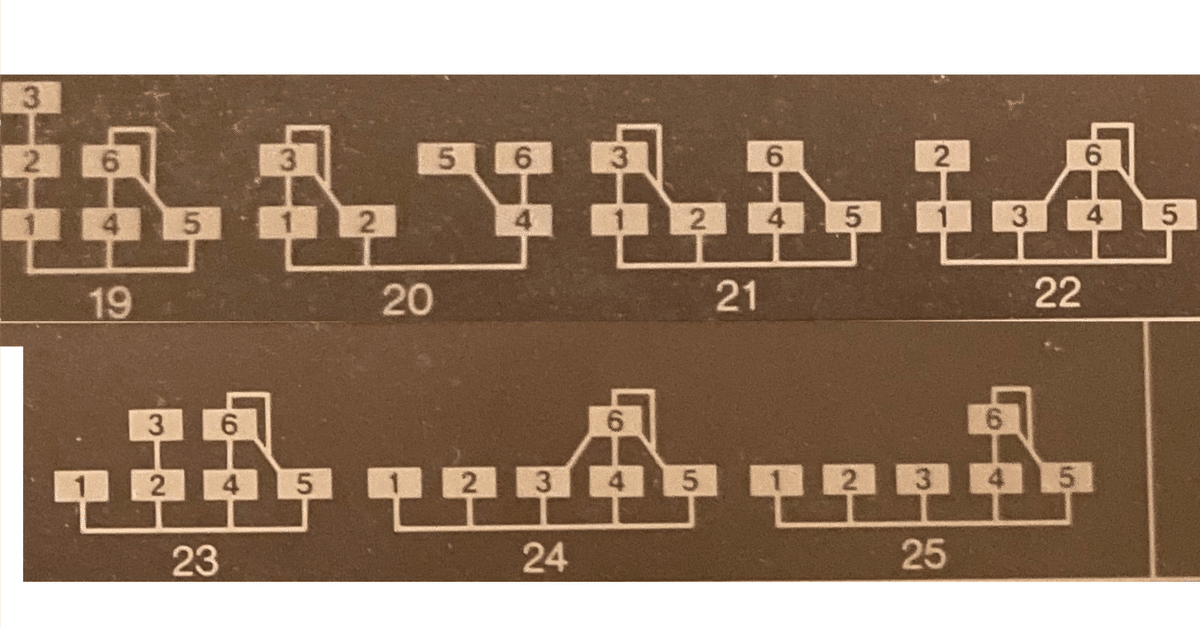
その中でも最も問題と思われるのがDX7の「アルゴリズム」一覧の19番~25番である。これらに共通する「1つのモジュレータが複数のキャリアを偏重する」構図を分かりやすく「モジュレータ共有」と呼ぶことにしよう。
この「アルゴリズム」は避けるべきである。これらを使うことでFM音源やスピーカーを痛めるみたいな危険は無いが、メリットがほぼ皆無と言ってよい。その理由は数学的に説明できる。とはいっても、難しい計算は一切無いので、文系や音大の方も安心して読んで欲しい。
要点をまとめると
モジュレータの強度と時間変化が共有されるので、変化のバリエーションに乏しくなる。
キャリア1とキャリア2の周波数が近い(厳密にはもう少し条件があるのだが)場合、うなり(音量の変化)になるのでLFOをキャリアにかけた方が有用である。
キャリア1とキャリア2の周波数が離れている場合は、お互いの倍音の穴を埋める形になり、耳に障る音になる。
1番は直感的に理解できるだろう。2番以降は数学的な説明が必要になる(が、難しい数式は出てこない)ので少し付き合ってほしい。
説明1:FM音源の倍音とは?
そもそも、FM音源の倍音はどのように決まるのだろうか。サイン波を使用した場合に関して、チョウニング博士がFM合成を発案した際に理論的に求められている。
$${f_n = f_c + n×f_m}$$
ここでnは任意の整数、$${f_c}$$はキャリアの周波数、$${f_m}$$はモジュレータの周波数である。ここでnが負の値をとるが、その場合は逆相のサイン波と考えられる。nが0の場合は当然キャリアの周波数がそのまま出ている。例えば、$${f_c = 5, f_m = 8}$$とした場合、$${-3 ≦ n ≦ 3}$$の範囲では$${f_n = -19, -11, -3, 5, 13, 21, 29}$$ となる。アナログシンセと違い、変調強度は倍音周波数に関わりが無いので、安定したサウンドが得られる。
倍音の振幅は第1種ベッセル関数 $${J_n(x)}$$という複雑な関数(ここで$${x}$$は変調強度)で求められるが、今回は全くと言っていいほど重要でないので、$${k = - n}$$が整数の場合、ベッセル関数$${J_k(x) = (-1)^nJ_n(x)}$$が成り立つことだけを覚えておけばいい。つまり1減るごとに符号が入れ替わることを除けば線対称である(数学的に妥当とは言えない説明で申し訳ない)。
説明2:うなりはなぜ起こるの?
うなりは音波の干渉である。高校物理で波の干渉をやった方も多いだろう。簡単に言えば2つの周波数がある場合、その周波数の差がうなりの周波数になる。つまり、100Hzと102Hzのサイン波が重なった場合は2Hzの周期でうなりが発生する。
勘の良い方ならお気づきかもしれないが、説明1で紹介したFM音源の倍音でもうなりが起こる。例えば$${f_c = 5.1}$$, $${f_m = 8}$$とした場合、$${-3 ≦ n ≦ 3}$$の範囲では$${f_n = -18.9, -10.9, -2.9, 5.1, 13.1, 21.1, 29.1}$$ だ。$${f_c = 5}$$, $${f_m = 8}$$ のFM波形と合わせると、正負両方とも0.1の周期(あえて単位は付けない)でうなりが発生していることが分かる。
しかしうなりと認知できないほど高い周波数だったらどうなるだろう。$${f_c = 500, f_m = 800}$$の場合$${f_n = …, -1900, -1100, -300, 500, 1300, 2100, 2900, …}$$で、$${f_c = 300, f_m = 800}$$の場合$${f_n = …, -2100, -1300, -500, 300, 1100, 1900, 2700, …}$$となる。両者のキャリアの音量が同じ場合、300Hzと500Hzなどのシリーズが同じ倍音は全く同じ振幅になる。つまり不自然な倍音の連なりが生まれる。
元波形自体で相殺などが発生する場合
「要点をまとめると」の2番で「少し条件がある」と言ったが、それに該当する場合が見出しのとおりである。例えば$${f_c = 1, f_m = 1}$$の場合は$${f_n = …, -2, -1, 0, 1, 2, 3, 4, …}$$という具合なので、正負の周波数が干渉することになる。例えば$${f(0) = 1}$$と$${f(-2) = -1}$$では打ち消し合う(ここで$${f(n)}$$はn番目の倍音の周波数。どうやらマイナスの数を小さくすることができないのでこのような書き方をしている)。この辺りは計算が難しいので、説明のために作成したodfを参考に、手作業で計算してもらいたい。
相殺・強調が発生する周波数比率は$${f_c : f_m = n : 1}$$ および $${n : 2}$$である。ここではシンプルに$${1 : 1}$$の場合を考えるが、他の場合も同じだ。
$${f_c = 1 + a, f_m = 1}$$とすると、$${f_c : f_m = 1 : 1}$$の倍音と対応しない倍音が出てくる。例えば$${f(-1) = a$$ となるが、aが十分低い場合は可聴域外の超低音であり、実用上は無視できる。
まずは倍音$${n}$$が正の場合を考える。$${f_c = 1, f_m = 1}$$の場合は$${f(n)}$$に打消しの作用があり、$${f_c = 5, f_m = 8}$$と違い$${f(n)}$$が$${f_c = 1 + a, f_m = 1}$$と対応しない。つまり、各々の倍音で、それぞれの振幅に合ったうなりが起こっている。
$${f_c = 1 + a, f_m = 1}$$ の倍音が負の場合もうなりが起こる。この場合、$${f_c = 1, f_m = 1}$$の$${f(n)}$$と$${f_c = 1 + a, f_m = 1}$$の$${f(-n -2)}$$が干渉することになる。
長いこと議論してきたので、複雑怪奇なカオス(実際制御不能だ)が発生しているような気がするが、「うなる」の一言で片づけられる。
なんでこんな「アルゴリズム」が生まれたのか
このように、中学程度の数学センスと物理知識があれば、モジュレータ共有「アルゴリズム」を採用する理由がほとんど無いことが理解できることはお分かりいただけただろう。おそらく今までのもやもやが晴れてスッキリしたFM音源プログラマーもいらっしゃるはずだ。
では何でこんな「アルゴリズム」が生み出されたのだろうか? 「キーボードマガジン2013年Summer」35ページによると、ヤマハの西元哲夫さんが決めたようだ。
いろんな音作りを私自身やってみて、これくらいの数だったらいいだろう、というのが32種類なんです。
要は地道な研究、努力と蓄積である。西元さんの経歴が詳しく乗っているわけではないので分からない部分はあるが、おそらく理系ではなく、ミュージシャン側の人物ではないだろうか。間違っていたらごめんなさい。
音楽を嗜むものとして、理屈的に正しいことが常に正しいことではないということは知っている。ただ、楽器作りには理屈をないがしろにしないでほしかったとも思うのだ。
この記事が気に入ったらサポートをしてみませんか?
