ABC335をpythonで解く
週1で記事を書こうと思うと、ABCの解説?らしき記事を書くのが楽だということに気づいてしまった。僕が解けた問題を解説?する。解けなかった問題は気が向いたら追記する。
問題文はAtCoder Beginner Contest 335(Sponsored by Mynavi) - AtCoderを見てください。画像はcarbonで作ってます。コードのコピーは出来ない?ので、もしコピーしたい場合はmuseのAtCoder提出結果まで来てください。
A
最後の文字の3以外に4を足したものを出力。

B
これで大体行くかなー、って感じのコードを書いたらまんまこれでAC。

C
頭の位置を覚えておけば、パーツiの位置はi-1ターン前の頭の位置にあることになる。初期状態として頭は(N,0)から(1,0)まで移動してきたところで開始したと考えれば楽に書ける。

D
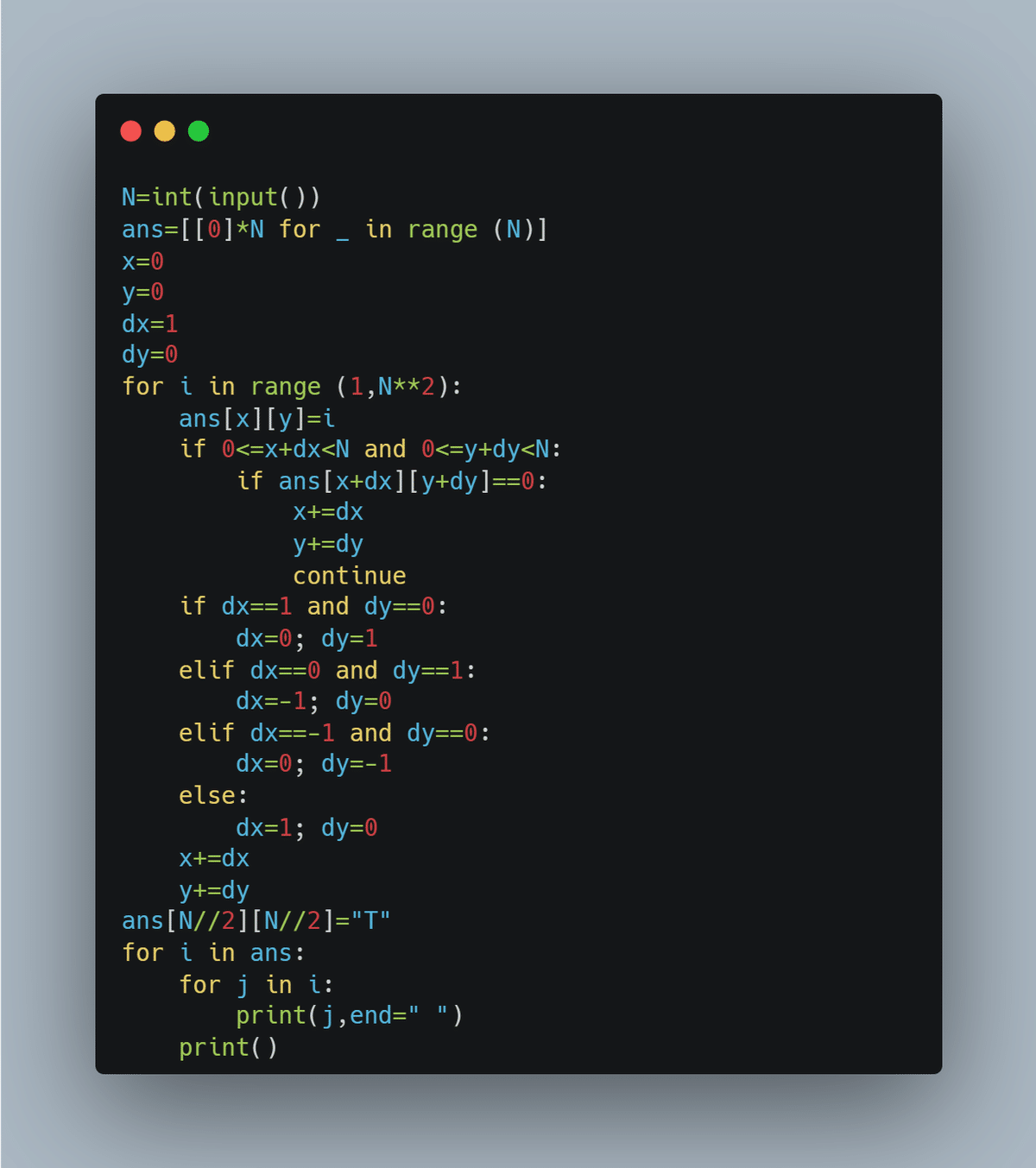
ABCでは珍しい構築問題。ぐるぐる渦巻き状に数字を埋めていく感じにすればok。
E
Aの大きさが小さいことを最優先に、今までに通ってきたパスに含まれる整数の種類数が多いことを第二優先に設定して、ダイクストラの要領で探索する。

F
前からパターン数求めていくdp解を普通に実装すると以下のようになる。O(N**2)解なのでTLEになるだろう。どうやって短縮するか分からなかったのでここでギブアップ。

公式解説を見ると、平方分割するとO(N**(3/2))になってTLEにならないらしい。というわけで以下のように書いた。上で説明していなかったが、pata[i]にはマスiで終わるようなパターン数を貯めている。
dpを配る際、A[i]の値がN**(1/2)以下になる場合はpataを更新せずに取り敢えずamaripata[A[i]-1][i%A[i]]に貯めておく。
すると、冒頭でpata[newi]を眺めたとき、A[oldi]がN**(1/2)以下であるようなoldiの中に本来pata[newi]が受け取っていなければならなかったパターン数pata[oldi]が含まれている可能性があるので、pata[newi]+=amaripata[j-1][newi%j]を1からN**(1/2)までのjに対して行い、受け取る必要がある。
この、冒頭でpata[i]にamaripataの情報を加える作業にO(N**(1/2))かかり、また、A[i]の値がN**(1/2)より大きかった場合のdpを配る作業にO(N**(1/2))かかるので、1回のループにかかる時間をO(N**(1/2))に抑えられる。賢い。
ちなみにamaripataをdictで書いたらTLEになったので横着せずにリストで書こう。

G
ガチガチの数学問題。詳しい証明は公式解説に任せ、雰囲気を書く。
mod Pの世界において、1以上P未満の整数A[i]のn乗が1になるような最小の自然数nは、必ずP-1の約数になり、このnをA[i]の位数という。
各A[i]の位数を求める上でポイントなのは、n,mをP-1の約数として、もしA[i]の(P-1)/n乗も(P-1)/m乗も1になるとしたら、A[i]の(P-1)/(lcm(n,m))乗も(多分)1になるということです。
だから、初期状態M=P-1とし、P-1の各素因数pに対し、もしA[i]のM/p乗が1になったらMをM/pで置き換える作業を繰り返したら、残ったMがA[i]の位数になっているのです。結構雑な作業で位数って求められるんですね。代数すげー。
また、答えを求めていく上でポイントになるのは、位数nの整数A[i]を1乗したもの,2乗したもの,……,n乗したものを列挙すると、位数がnの約数になっているような整数A[j]はこの列挙された中に必ず含まれ、位数がnの約数でないような整数A[j]は必ず含まれないことです。代数すげー。
つまり、位数nの整数がAに何個あるのかを貯めたものを作れば、Pの約数の個数の2乗のオーダーで答えを求められます。

試しに書いてみたけど、全然解説してないやん。まあ取り敢えず記事を書いたので偉い。(ホンマか?)
この記事が気に入ったらサポートをしてみませんか?
