
プログラミングで苦労しないためのノウハウ
はじめに
皆さん、こんにちは。
今回は、私がプログラミングの際に気を付けていることを、僭越ながら、紹介させていただこうと思います。
自分自身の備忘も兼ねています。
プログラミングとは
そもそものプログラミングに関する説明は、以下の記事にて行っておりますので、よかったら参照下さい。
参考までに、小職のプログラミング歴について…
尚、私がおおよそ、どのくらいの期間、何をやってきたかを紹介させていただきます。
先ず、金融系の保守運用開発にて、システムエンジニアとして、プログラミングを8年程行ってきました。
その後、機械学習ブームの波に乗る形で、データサイエンティスト/AIエンジニアとして、プログラミングを9年程行ってきました。
それだけやって、ようやく半人前になれた位かと思っております。
最近では、大きなストレス無く、プログラミングを楽しめています。
プログラミングのノウハウについて
半人前の私ですが、かつての同僚に教えてもらったノウハウや、自分自身で編み出したノウハウなどが、それなりに溜まってきていますので、ここに記載させていただきたいと思います。
特に前者が、紹介させていただきたい/残したい内容となります。
尚、私が最近使用しているプログラミング言語がpythonである為、以降の記載はpythonをベースとさせていただきます。
ノウハウは、抽象的に書かせていただくと、大きく以下となります。
(1)いきなりプログラミングを始めず、先ずは紙に書く
(2)debugをしやすいnotebook環境にて、結果を確認しながらプログラミングを進めていく
(3)実装途中で、しつこいくらいに確認を挟む
(4)いきなり関数を書かずに、先ずは直列1ストリームで書く
(5)よく使う関数を、自分の引き出しにストックしておく
(6)極力、for文やif文を使わないようにする
(7)分かり易さのために、不要なコードを敢えて書く
以上。
以降で、1つずつ紹介をさせていただきます。
ノウハウ(1) : いきなりプログラミングを始めず、先ずは紙に書く
プログラミングを行う際に、やってしまいがちなのは、「え〜っと、〇〇が△△になって…」という想像をしながら、とりあえずポツポツとコードを書き始めてしまうことです。
もし、頭の中のイメージが、非常に鮮明である場合には、そのような着手の仕方でも良いかと思います。
例えば、同様のプログラム内容を、何度も記載した経験があるような場合です。
逆に、少しでもイメージがボヤけているような場合には、いきなりコードを書き始めず、先ずは、紙などに考えを整理することをオススメします。
例えば、2変数の連立方程式を、加減法で解く場合で考えてみましょう。
加減法をご存知でない方は、以下の記事が分かりやすいので、参照いただけたらと思います。
この解法実施を、プログラムによって自動化したいと思います。
その際、実際に解き始めるとスラスラと解ける方でも、プログラムに解き方を実装しようとすると、手が止まる方が多いかと思います。
そうした際には、先ず、紙に解き方を書いてみることをオススメする形です。
(問題)
4x - 3y = -9
3x - 7y = 17

こうすると、何を、どういう順番で行う必要があるか、思考がクリアになると思います。
プログラミングをする上では、それが大事です。
こうして思考をクリアにした上で、書いてみたプログラムが、例えば、以下となります。
import numpy as np
# 左辺の係数と、右辺の値を、変数にセットする…
f_1 = np.array([4, -3, -9])
f_2 = np.array([3, -7, 17])
# x項の係数を、お互いに掛け合う…
f_1_ = f_1 * f_2[0]
f_2_ = f_2 * f_1[0]
# 式同士の引き算を行う…
diff = f_1_ - f_2_
# yを求める
y = diff[2] / diff[1]
# 求まったyの値を、何れかの式に代入するイメージで、xを求める…
x = ((-f_1[1] * y) + f_1[2]) / f_1[0]
print('x =', x)
print('y =', y)この行為を、システム開発では一般的に、設計と呼びます。
設計は、緻密に行えば行う程、プログラミングの手戻り/ミスを抑える効果があります。
机上にて、想定を整理することにも役立ちます。
設計のアプローチは一般的に、ケーススタディやペルソナと言いますか、実際に幾つかの問題を手で解いてみて、そこから共通の解き方を導出する形が多いかと思われます。
一方、設計には時間を無限にかけられると言いますか、大枠の解き方を導出するのは簡易であるものの、想定を漏れなく洗い出すことが困難であったりします。
つまり、プログラムを実装してから、沢山の問題でテストしてみて、動作を保証する方が、効率が良いということです。
その辺りのトレード・オフとの向き合いについては、経験を重ねて、良いバランスを取れるようになると、良いかと思います。
設計を行うことのメリット
- プログラミングの誤りを、事前に抑えることができる
- プログラミングにかける時間を、短縮することができる
設計を行うことのデメリット
- 事前の想定を考察することに時間をかけ過ぎてしまうことがある
(ある程度の複雑さからは、プログラムでテストをする方が効率が良い)
ノウハウ(2) : debugをしやすいnotebook環境にて、結果を確認しながらプログラミングを進めていく
先程、紹介したプログラミングを再掲します。
import numpy as np
# 左辺の係数と、右辺の値を、変数にセットする…
f_1 = np.array([4, -3, -9])
f_2 = np.array([3, -7, 17])
# x項の係数を、お互いに掛け合う…
f_1_ = f_1 * f_2[0]
f_2_ = f_2 * f_1[0]
# 式同士の引き算を行う…
diff = f_1_ - f_2_
# yを求める
y = diff[2] / diff[1]
# 求まったyの値を、何れかの式に代入するイメージで、xを求める…
x = ((-f_1[1] * y) + f_1[2]) / f_1[0]
print('x =', x)
print('y =', y)設計によって、このプログラムが、比較的スラスラと書けるようになると、前章で説明しました。
しかし、実際には、これらのコードを一気に実装するのは難しかったりします。
「あれ、ここまでのコードで、どこまでの処理が表現できてるんだ…?」と、頭の整理が付いていかなくなってしまったりします。
思考としては、将棋の先の手を幾つも想定することと、似ているかと思います。
想定が積み上がりすぎると、考えるのが辛くなってきます。
そこで、私のオススメは、jupyter notebookを使用することです。
jupyter notebookを使用すると、思考の積み上げは、比較的簡単に行うことができます。
尚、インストール方法と使用方法の説明については、別の記事に書いておりますので、よかったら参照下さい。
先程のプログラムを実装するような場合、jupyter notebookでは、任意の処理の単位にて、区切ることができます。
そして、任意の処理の単位での結果を、随時可視化すると、思考の積み上げが楽になります。
例えば、以下のような形です。

途中結果が逐一確認できるので、「よし、ここまでは上手くいっている…。さて、ここから…。」という風に、考えを進めていけるのです。
そうして、考えを進めていった後、各セルに書いてあるコードを集約して、以下の形にまとめれば、先程紹介したプログラムができあがる形となります。

ノウハウ(3) : 実装途中で、しつこいくらいに確認を挟む
尚、プログラムをまとめ上げる前でも後でも、可能な限り、プログラムの結果は確認することをオススメします。
BUGが予期せず、潜み込むためです。
当然のように、ミスをしないと思っている箇所でも、或いは、そうやって油断している箇所ほど、BUGを埋め込んでしまったりします。
プログラムの出力確認は、理想的には、全ての出力内容に対して行うことが望ましいです。
前述の処理などは、そのようにしています。
一方で、出力が複数件に渡る場合や、出力要素数が多数に渡る場合については、それが難しくなる時があると思います。
その際は、代表の数件を覗いたり、統計量を確認するなどすることをオススメします。
例えば、pythonのnumpyライブラリに用意されている、「np.random.rand()」関数の出力について、検証してみることにしましょう。
「np.random.rand()」関数は、0〜1までの数字を、確率の偏り無く、完全ランダムに出力する関数です。
優秀な老舗ライブラリである為、間違いは無い筈ですが、これを自分がコーディングしたものとして、試しにチェックしてみましょう。
先ず、値域が本当に0〜1に収まるか確認してみましょう。
試しに、100個生成してみます。
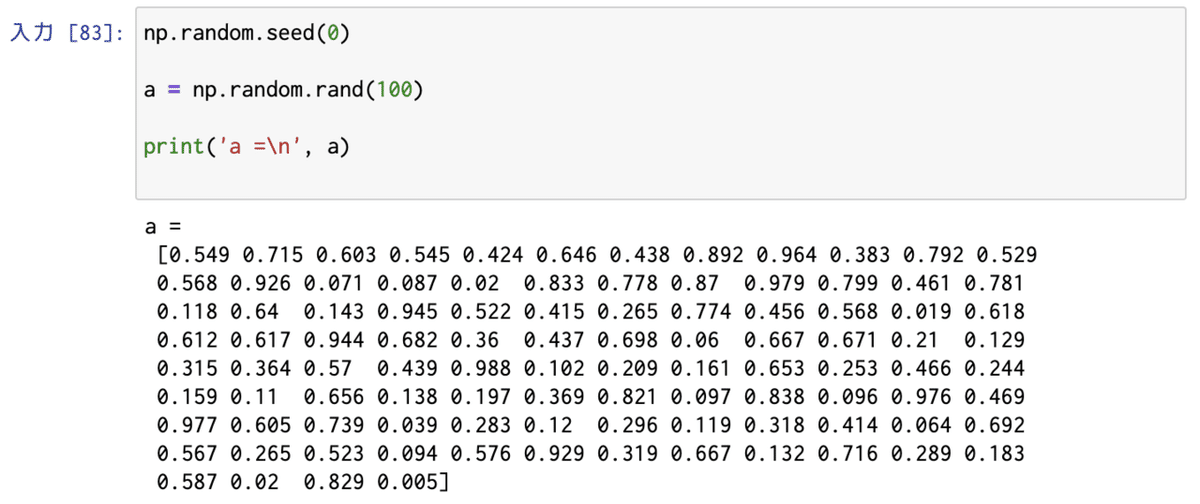
この位のデータ件数であれば、目検で確認できないことはありません。
とりあえず、100個生成した限りでは、値域が0〜1にちゃんと収まっているようです。
更に確証を得る為、1,000個、10,000個などでも確認したいところですが、その位のデータ件数になってくると、目検で確認することが難しくなってきます。
例えば、10,000件の内、100件を無作為に取り出して、それが合っていれば良しとする、という判断基準も悪くないですが、可能であれば厳密に担保をしたいところです。
そこで、統計量を用います。
統計量の最も一般的な指標は、最小値、最大値です。
それが分かれば、値域の検証は事足ります。
やってみます。

乱数を10,000個作った際の、最小値は約0.0001、最大値は約0.9999ということが分かりました。
更に件数を増やして、乱数を100,000,000個(1億個)作った際でも、確認してみます。

乱数を100,000,000個(1億個)作った際の、最小値は約0.00000001、最大値は約0.99999999ということが分かりました。
やはり、値域については、厳密に問題が無さそうです。
次に、確率の偏りが無いという仕様を疑ってみましょう。
本当に偏りが無いかどうか。
有名な統計量である、平均値でそれを推し量ってみます。
例えば、0〜1の数字が偏り無く生成されるのであれば、平均値は0.5に近くなる筈です。
サイコロの出目の平均が、3.5に収束してくるのと同じ要領です。

最大値/最小値を同じ要領で計測してみると、平均値は約0.4999であることが分かりました。
どうやら0.5に収束している様子です。
しかし、ひょっとすると、0.5を中心とした偏りが発生しているかもしれません。
つまり、本当は偏りがあるんだけど、平均としては0.5となっている可能性です。
その点について、確認を取るには、最強の確認方法である図示化を行います。

用いたのは、matplotlibという図示化ライブラリにある、histという関数です。
細かく区切った値域毎の、該当件数を図示化してくれるものです。
この図を見ると、なるほど、確かに等間隔に乱数を発生してくれていそうだ、というのが見て取れます。
こういった確認を、プログラムの実装を進める毎に、随時実施することをオススメします。
また、jupyter notebookは、上記のような確認を、随時実施しやすい実装形式となっています。
ただし、見てもらって分かるように、精緻に確認しようとすればする程、或いは、確認対象や確認ポイントが複雑である程、確認に労力を要することとなります。
確認精度と、実装速度のトレードオフ、とも言えるでしょう。
その意味では、アルゴリズムを把握した上で、「どんな確認が取れれば、この処理は担保ができるか…?」という確認ポイントを、なるべく軽くするように考えを巡らすことが肝要です。
そこのカンコツは、プログラマーの腕前の差別化ポイントになろうかと思います。
尚、この確認は、料理でいうところの味見のようなものです。
或いは、飲食系職の経験のある方に言わせると、毒味でもあるだろうということです。
また、一流の料理人ほど、味見は欠かさずに行うようで、プログラマーとしても、出力内容確認は欠かさず行うことが一流への近道であろうと、個人的に思うところです。
ノウハウ(4) : いきなり関数を書かずに、先ずは直列1ストリームで書く
プログラミングには、関数というものがあり、それも思考整理には便利です。
pythonにおける関数については、以下などが分かりやすいかと思いますので、ご存知でない方は参照下さい。
例えば、先程の処理を関数化すると、以下のように書けます。
def solve_renritsu(f_1, f_2):
# x項の係数を、お互いに掛け合う…
f_1_ = f_1 * f_2[0]
f_2_ = f_2 * f_1[0]
# 式同士の引き算を行う…
diff = f_1_- f_2_
# yを求める
y = diff[2] / diff[1]
# 求まったyの値を、何れかの式に代入するイメージで、xを求める…
x = ((-f_1[1] * y) + f_1[2]) / f_1[0]
return x, y
# 左辺の係数と、右辺の値を、変数にセットして、解く…
f_1 = np.array([4, -3, -9])
f_2 = np.array([3, -7, 17])
x, y = solve_renritsu(f_1, f_2)
print('x =', x)
print('y =', y)solve_renritsuという関数を用意して、それを呼び出すことで連立方程式が解ける形です。
定義を一度してあげれば、何度でも再利用が可能なので、以下のように別問題への適用も簡単に行なえます。

或いは、関数は定義範囲/スコープが自由ですので、以下のように記載することもできます。
def solve_y(f_1, f_2):
# x項の係数を、お互いに掛け合う…
f_1_ = f_1 * f_2[0]
f_2_ = f_2 * f_1[0]
# 式同士の引き算を行う…
diff = f_1_ - f_2_
# yを求める
y = diff[2] / diff[1]
return y
def solve_renritsu(f_1, f_2):
# yを求める
y = solve_y(f_1, f_2)
# 求まったyの値を、何れかの式に代入するイメージで、xを求める…
x = ((-f_1[1] * y) + f_1[2]) / f_1[0]
return x, y
# 左辺の係数と、右辺の値を、変数にセットして、解く…
f_1 = np.array([4, -3, -9])
f_2 = np.array([3, -7, 17])
x, y = solve_renritsu(f_1, f_2)
print('x =', x)
print('y =', y)こうすることのメリットとしては、どこか別の処理にて、solve_yが再利用される場合などです。
一方で、ソースが読みづらくなったと感じる人もいるかと思います。
或いは、コードに誤りを含んでしまった場合で、想定外の結果が出力されてしまった時に、どこにコードの誤りがあるのかを追いづらかったりします。
ここに関して、私のオススメとしては、先ずはnotebookなどにて、関数を極力使わずに実装をすることです。
もう少し言えば、先ずは極力、段落下げ/ネストをせずに実装を行うことをオススメします。
といいますのも、いきなりキレイなコードを書こうとして、関数を実装し始める方がいらっしゃる為です。
ここは、実装方針の柔らかいところで、一概に言えないのですが、個人的な所感としては、そのアプローチはコードの誤りを混入させやすいかと思います。
そして、コードの誤りを追いづらく。
更に言えば、自分以外の方が実装した関数を拝借する場合に、単なるI/Oとして、中身を確認せずに使用してしまう傾向が強くなるかと思います。
尚、これは、かつての現場の先輩から、教えていただいたノウハウになります。
著名な研究者の方だったのですが、アルゴリズム理解について、徹底しておりました。
実際に、私がデータサイエンティスト/AIエンジニアとして働く上で、このエクササイズは糧となっています。
ノウハウ(5) : よく使う関数を、自分の引き出しにストックしておく
前章の関数の話については、段階があるという話をさせていただきました。
先ずは、関数無しで記載する流れが経て、次に、汎用的な共通処理を関数化するという流れです。
しかし、何れの場合においても、必ずその流れに沿うことをオススメする訳ではありません。
初めて向き合うアルゴリズムについては、そうすることでミスを減らしたり、理解が深まったりという効能があるという形です。
例えば、何度も繰り返し実施してきていて、要領を得ている処理については、積極的に関数を適用すべきだと思います。
その意味では、関数化に至るまでには、幾つかの段階があるかと思います。
例えば、以下などです。
(い) 先ず、最初の実装時は、関数化せず
(ろ) その後、一定の取組内で、ある一定の処理が、複数回実行された為、関数化
(は) 更にその後、別の取組においても、その関数を用いた為、Evernoteなどのメモツールに、関数コードを保存
(に) 更にその後、また別の取組においても、その関数を用いたが、少し機能を足す必要があった為、汎用的に改良
(ほ) 更にその後、自分以外のメンバーから、その関数を使いたいというリクエストがあった為、リファクタリングを行い、GitHubリポジトリにて公開
私がオススメしないのは、いきなり(ほ)を始めたりすることです。
または、初めて向き合うアルゴリズムについて、(い)や、(い)に相当する検証をスキップして、(ろ)以降に取り組むことです。
尚、上記にEvernoteの記載がありますが、私のオススメになります。
ネットに繋がっていれば、いつでもどこでも引っ張り出せるので便利です。
ただし、言わずもがな、機密情報などをEvernoteで取り扱うことはオススメしません。
あくまで、generalな関数の管理についてのオススメになります。
ノウハウ(6) : 極力、for文やif文を使わないようにする
プログラムを書いていて、頭がゴチャゴチャしてくる理由のTOP1は、個人的に関数があっちこっちに飛ぶことかと思います。
次いで、TOP2/3が、for文とif文かと思います。
for文と、if文は、プログラムで行いたい自動化のコアとなる概念です。
それらは、自動化を、複数対象に適用するための繰り返しという概念と、人間が下す判断を模倣するための条件分岐という概念になります。
また、AIについては、誤解を恐れずに言えば、if文による判断をより高度に人間らしくするための機能となります。
そんなfor文とif文についてですが、処理が流てきた際の想定については、頭で想像するしかありません。
例えば、以下のような場合です。

20個ずつの乱数を持つ、2つのベクトルに対して、各要素が0.5以上であるか、その逆であるかを判断しているif文があります。
そして、そのif文を、データ要素毎に適用するためのfor文があります。
この時、for文のネストや、if文のネスト以下の処理は、セルの中から取り出すことができません。
もし、if文の分岐によって処理が異なるようなアルゴリズムを適用する場合、上記の1セル内にアルゴリズムを詰め込む必要があります。
詰め込むアルゴリズムが複雑である程、セルに書き込む処理が多くなり、思考整理が難しくなってきます。
では、思考整理をしやすくするためには、どのように対処すればよいでしょうか。
ヒントは、特にpythonにおけるif文の仕組みを理解することにあります。
それは、if文に記載されている条件式の返り値が、booleanであるということです。
printしてみると、分かりやすいです。

各要素は、TrueかFalseのboolean型であり、if文はTrueであれば通し、Falseであれば弾くということを行っています。
尚、このbooleanの値は、numpy型の配列であれば、事前に計算することができます。
以下のような形でです。

また、先程のif文は、&演算子を使うと、ネストを1つ減らすことができます。

そして、「(a[i] >= 0.5) & ~(b[i] >= 0.5)」というbooleanについても、事前に一括導出ができます。

このbooleanを使って、選定されたaとbに絞り込むためには、以下のように行います。

for文とif文とを使わずに、同じ結果を得ることができました。
これは、numpy配列を用いることで実現が可能となる処理です。
イメージとしては、料理を1皿ずつコツコツと仕上げるか、お皿を大量に並べて一気に作り上げていくのか、という違いになります。
一概に、今回のような実装方法が適用できないケースもあろうと思いますが、できる限り処理を区切って結果確認という形に持っていくことで、コードの誤りを未然に防ぐことができると思います。
或いは、読みやすいコードに仕上げることができるかと思います。
尚、numpyを使って、処理をまとめ上げますと、一般的に高速化が実現されます。
それについては、別途記事を書いていますので、よかったら参照下さい。
尚、for文に関しては、以下のような方法で確認を取ることも良いかと思います。

一度、繰り返しを外し、任意の添字をセットして、処理を行ってみる形です。
上手く処理が行えていそうであれば、繰り返しを適用します。
ノウハウ(7) : 分かり易さのために、不要なコードを敢えて書く
最後のプログラミングノウハウですが、これは私が若かりし時に、先輩から教えていただいたものとなります。
考え抜かれた独自のノウハウによって、プログラムへのバグ混入を未然に防ぐ、プロフェッショナルな方でした。
そのノウハウは、コードを実装した時点で、その確実性を徹底して向上するというものでした。
例えば、以下のようなコードがあったとします。
![]()
この結果は、幾つになるでしょうか?
答えは以下です。

これは、足し算よりも、掛け算を先に計算する為に、このような結果が出るものとなります。
仮に、演算子を無理やり左から順に計算させようとすると、以下となります。

これは、小学校の頃にやった算数でそう習っていると思いますので、当たり前の感覚だと思います。
それでは、このコードの結果はどうなるでしょうか?

結果は、以下となります。

「>=」や「<」の演算子と、「&」という演算子について、計算の順序が分からないというエラーになります。
このコードは、以下のように書き直さないと、エラーが解消しません。

つまり、計算のスコープを、括弧によって限定する形です。
先にbooleanを求めてもらった後で、「&」演算子を適用するように促します。
それでいうと、先程の足し算掛け算に関しても、プログラムの仕様はあれど、以下のように記載してあげることが親切だったりします。

尚、関連する話として、以下の記事は面白いと思いました。
(題名から、面白い…!w)
また、pythonのコーディング規約であるpep8には、その辺りについて明記されていないものの、規約等に準拠することでコードの可読性を下げることを推奨しない旨が、記載されていたりします。
この辺りのバランスは、時間をかけて成熟していただけたらと良いかと思います。
まとめ
以上で、プログラミングの個人的なノウハウの紹介を終えます。
まとめとしましては、以下になるかと思います。
(A) いきなり作り込み過ぎない
(B) テストは極力徹底する
(C)numpyをベースに最適化すると、思考も整理され、高速化もされる
以上です。
特に(C)に関しては、numpyの秀逸さに感嘆するところ、或いは、numpyが参考にしているであろうMATLABの秀逸さに感嘆するところです。
近年のAI系技術の躍進、特に、Deep Learningの躍進は、このMATALBからnumpyへと続くアルゴリズム感の上に成り立っていることは、間違いがなかろうと思います。
MATLABが好きな方は、以下のnumpyリファレンスが面白いので、是非参照なさって下さい。
おわりに
ここまで読んで下さった方、ありがとうございました。🙇
プログラミングを学んでいる方の後押となれましたら幸いです。
