
【薄膜】ぬれの強調に関わるフラクタル表面構造
今回は薄膜において、水をはじく効果を劇的に高めるフラクタル構造について解説します。
何となく興味を持った人、フラクタルや薄膜という言葉に釣られた人向けに作っているつもりです。つまり初学者向け。
今回の話は辻井薫先生の次の論文、本を基に作成しているので、事前に目を通しておくことを推奨します。
本文中では[]で囲った部分に参考文献のリンクを紐づけてあります。
間違いや疑義があればコメントしてください、速攻直します。
ぬれの基本
ではまず、濡れ性についておさらいしましょう。
固体表面での液体の広がる現象、これを「濡れ」といいます。
(濡れ広がるというよね)
ここで、濡れやすい、濡れにくいという「濡れ」を定量的に示す物理量が、固体表面の水滴がとる角度、「接触角」になります。
接触角はYoung(ヤング)の式と呼ばれる「静止した液滴の接触角と、液体、気体、固体の表面張力の関係を表した式」で示されます。

γは表面張力で、S(Solid:固体)、L(Liquid:液体)、SL(固体と液体)はそれぞれ固体の表面張力、液体の表面張力、固体と液体の界面張力を示します。
(本来ならばγsやγlも固-液、気-液で書くのでsgとかlgの界面張力なんですが、簡単にしたいのでこれにします)
表面張力と界面張力の区分けはかなり曖昧な感じがありますが、単体の張力であれば表面張力、固・液・気界面間での作用なら界面張力くらいの認識で良いです。
ちょっとした余談ですが、この分野を調べると時たま「表面エネルギー(表面自由エネルギー)」という言葉に出会うと思います。
これは固体での表面張力の表現として使用されているもので、表面張力とほぼ同義の言葉であるとお考え下さい。
これは単位でも分かるのですが、
表面自由エネルギー:[mJ/m^2]、表面張力:[mN/m]、J = N・m ですから
mN/m = (mJ/m)/m = mJ/m^2
という感じです。同じです、同じ。
ぬれ性議論において、実際はDupreの式というものをYoungの式と組み合わせたYoung-Dupreの式を用いて、固-液、固-固間の接着仕事を求めたりします。しかし、今回のフラクタル表面の話では使用しないので、参考を置いておきます。読んでみてください[1][2]
このYoungの式で、角度が10°以下であれば超親水、30°以下なら親水、150°以上なら超撥水、90°以上は撥水の扱いになります。
今更ですが、ここから先の接触角という言葉はすべて静的接触角とお考え下さい。
ここの接触角と親水、撥水の定義は媒体によりバラついていますが、そこまで重要な指標ではないのでここは何となくで覚えてもらって結構です。

撥水性を示す代表的な物質は、フルオロアルキル基を持つシリコーン、フルオロアルカンなどのフッ素材料になります。
-CF2-、-CF3で満たされており、非常に高い撥水能力を示します(パーフルオロアルキル~としてPFASという括りがある)

前者はシランカップリング剤として、強固な表面コーティングを与え、後者は界面活性剤として、撥水スプレーなんかに入っていたりします。
テフロンなんかも有名ですよね。
あ、因みに下の動画ですが、以前PFAS問題について多少取り上げたものです。気が向いたらどうぞ(雑ダイマ)
ですが、材料の表面張力は決まっており、最も低い表面張力を持つフッ素材料であっても、良い所120°近く[3]が限界になります。
この壁を越えて超撥水を実現するには、今まで利用してきた平滑表面ではなく構造を利用する必要があります。この構造利用はつまる所、凹凸を付ける、ということであり、現在見つかっている最高の構造が、タイトルにある「フラクタル表面」という事になります。
フラクタル構造がどんなものか、このnoteを見ている物好きな方なら殆どお分かりかと思いますが、同じ形が規則的に続いていき、一部が全体と自己相似な構造を持っている図形が「フラクタル」です。三角形をべたべたとくっつけて行ったらこうなりますよね(参照は下で)
フラクタル構造を機能性材料開発に用いて濡れ性を制御するのは、辻井らが1995年・応用物理学会誌 第64巻 第8号に掲載した「フラクタルの表面科学への展開」[4]が初出かと思われます(自分調べ)
辻井らによると、このフラクタル表面はアルキルケテンダイマー[5]と呼ばれるワックス材料で作成されているそうです。これは製紙用の中性サイズ材の原料として知られており、結晶化することでフラクタル構造が作成されることが確認されました。
この構造を用いることで表面積を増大させ、174°という圧倒的な接触角を得ることが出来ています。
このように構造を用いることで超撥水は実現できますし、フラクタル表面は着雪防止表面としても注目されていたりします。
180°に迫る超撥水でないにせよ、蓮の葉効果やモスアイに代表されるバイオミメティクスなど、表面微細構造自体は実用化されています。
しかしながら、フラクタル構造は注目されども、商用で実用化された例は現在までにありません。
表面汚染や強度の問題の解消が難しい事が原因です。これは微細構造全般に言える問題と言えます。
(蓮の葉構造が採用されるヨーグルトの蓋を削る前後の比較動画:[6]、[7])
アルキルケテンダイマーはワックス系ですから、摩耗や耐候性でに難があります。実際、この構造を破壊して同じように接触角を測定すると、109°程度の接触角しか示さない事が分かっています。今後金属のような材料でフラクタル表面を作成しても微細突起が経年劣化や摩耗で削られてしまうのは想像に難くありません。表面汚染で溝が埋まってしまうのも考え物です。
今後の研究に期待したいですね。
google schlorなんかでfractal surface wetとか調べてもいいかもですよ。
押さえておきたい濡れの理論について
では、ここからはより踏み込んだ話に移りたいと思います。
何故表面微細構造、凹凸が超撥水効果を示すかについてです。
そのためにはまず、次のYoungの式と同様に重要な、静的撥水性についての二つの理論を知る必要があります。
wenzel理論と、Cassie-Baxter理論と呼ばれています。
この2つの理論は前提として、表面は粗面で凹凸構造がある場合に適用される考え方です。
それぞれを見ていきましょう。
wenzel理論
まず一つ目のwenzel理論です。
このwenzel理論は、固体表面の凹凸が十分に小さい場合に適用されます。この微細凹凸の上に置かれた液体は、微細凹凸表面の隙間に浸透し、間を満たしていると考えます。
この「隙間を満たしている」状況では、凹凸構造によって、表面積が増える事に注目してみましょう。
凹凸構造により実表面積が倍に増えるという事は、固-気の表面積、固-液の表面積が増加していると考えられますよね?なので、その分ヤングの式の右辺をR倍します。

つまりここでこのような式となります。θrは粗面の接触角です。Rは見かけの面積に対する実際の面積で出すので、式は以下となります。
R=凹凸のある実際の表面積/見かけの表面積
Rは表面の粗さに伴い増加するので、常に1以上になります。
平らな面に着滴した水の接触角θを考えると
θ>90ではθr>θ
θ<90ではθr<θ
cosθが正か負かによって、cosθrはより大きな正か負の値になります。つまり、表面が粗くなれば濡れやすい表面はより濡れるようになり、はじく表面はよりはじくようになるということです。
ちょっとこれだけ聞くとよく分からないと思うので、計算してみましょう。
この平滑な表面を持つ板の上に水を落とすと、接触角が100°を示し、撥水とします。
ここに極微細な凹凸構造が出来たとして、見かけの表面積が10cm^2、凹凸表面積が15cm^2だとしてR=15/10=1.5となります。
ではこれをwenzel式に代入すると
cosθr=Rcosθ=1.5xcos100°≒-0.26
arccos(-0.26)ですから
θr=105°
という感じで、元の接触角よりも撥水になります。
では親水も見てみましょう。今と同じ条件で、接触角を60°とします。
cosθr=Rcosθ=1.5xcos60°=0.75
arccos(0.75)
θr=41°
となります。
表面が粗くなれば濡れやすい表面はより濡れるようになり、はじく表面はよりはじくようになるということがわかりましたか?
因みに、今設定した条件だと50°以下の接触角でRcosθ>1となり、この式は成立しなくなります。(cosθは取れる範囲が1≧cosθ≧-1なので…)
Cassie-Baxter理論
それでは次にCassie-Baxterの理論を見てみましょう。
この理論では、固体の平滑表面は、二種類の物質A、Bで出来ています。この表面は交互に並んでいて、つまるところのモザイク状の様相を呈しています。
つまり、2種類の物質ごとで液-固界面は変わりますから、これを式に表すと

となります。
この時fa,fbは物質A、Bの面積の割合(なので、fa+fb=1)で、θa,bはそれぞれの接触角です。
では、二種の物質で作られた平面で、一方が空気の時はどうなるでしょう?
この図のように、先程まであったBが抜けて空気が入り、凹凸面が出来ます。
この凹凸面はwenzel理論の時よりも深く、水は毛管現象で溝の奥まで到達できません。水滴の下に空気の層があることになります。
空気と水の接触角は180°であることから、θb=180°になります。
(大気中で水滴は表面積が最小になうとします。宇宙では水は球の形になりますよね)
まとめるとθb=180°、fa+fb=1よりfb=1-faなので
以下の式が得られます。
cosθr=fa cosθa + fb cos(180°)
=fa cosθa -1(1-fa)
=fa cosθa + fa - 1
となります。

この時、faの面積の比率が小さければ小さいほど空気側に偏ることになるので、式中では-1に値が近づきます。cosθ=-1は180°ですから、より撥水によるという事です。
これを満たす構造は、より空気を含んだ構造ですから、針の先端ように尖った小さい柱を立てた構造を作れば、その表面は180°に近い接触角が得られることを意味していると言えます。
これらの式にはいくつかの修正案があり、wenzelとCassie-Baxterの転移点、この凹凸形状による差異など細かく詰める部分は沢山あるのですが、今回は主題から逸れるので割愛します。
要点
ということで、以上の二つの理論をまとめると次のようになります。
■wenzel理論
・cosθr=rcosθで示される。
・十分に小さい微細凹凸がある時、ぬれやすい表面はさらにぬれやすく、ぬれにくい表面はさらにぬれにくくなる事を意味している。
■Cassie-Baxter理論
・cosθr=fa cosθa + fb cosθbで示される。
・二種類の物質A、Bでモザイク状の表面を構成している。
・この時、どちらかの材料が空気である場合、f・cosθ + f - 1で示される。
・より空気の面積率が高い、針の先端ように尖った小さい柱を立てた構造を作れば、その表面は180°に近い撥水性が得られることを意味している。
フラクタル表面について
それでは、ここまでの理論を押さえた上で、フラクタル表面の濡れ性についてみてみましょう。
前述のようにwenzelの理論では、微細凹凸で見かけの表面積よりも実表面積が増加しぬれやすい表面はさらにぬれやすく、ぬれにくい表面はさらにぬれにくくなります。

フラクタル表面は無数の微細凹凸を持っています。凹凸に次ぐ凹凸、つまり、考えうる理想的な凹凸表面と言えます。wenzel理論に当てはめれば、フラクタル表面は莫大な表面積を持ち、とても濡れの強調が強いと言えます。
ここで、フラクタル表面上での接触角をwenzel式より表すと

この時、Lとlはフラクタル構造が成り立つ最大と最小の大きさであり、Dはフラクタル次元を指します。
この(L/l)^D-2ですが、これはフラクタル図形で有名なコッホ曲線より導けるものです。
先程から図で出している正三角形の連続がまさにコッホ曲線ですね。知っている方もいらっしゃると思います。
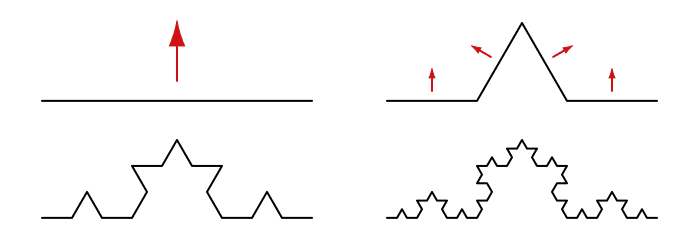
一本の線分を三等分して、真ん中を正三角形に折る。それぞれに出来た線分をまた三等分して真ん中を折る事を繰り返し、コッホ曲線を作成します。
この時、一回ごとに線全体の長さは4/3になりますから、(4/3)^nがコッホ曲線の因子になります。
この分子、分母が上記式のL、lに当たる事は分かって頂けるかと思います。
フラクタル次元Dの考え方についてですが、フラクタル図形の相似比が1:aである時、長さの比が1:b となる時のa^n=bとなるnのことをいます。なので、先程の図形ではa=3、b=4 となるので、
D=log4/log3で≒1.2618 、コッホ曲線は1.26次元の図形であることが分かります。[5]、[6]、[7]
コッホ曲線のようなフラクタル図形では入り組んだ折れ線の形をしています。
しかし、実際の粉体や薄膜の表面は二次元的ではなく、凹凸構造を持っています。
このことから、二次元的な長さだけではなく、三次元的な要素が絡み、2≤D<3 の次元 D で特徴づけられる凹凸表面のことをフラクタル表面としています。
上記式Dには2~3の非整数が入る事になります。
そして、-2を行っている理由についてですが、D=2 のときには0、0乗すれば値は1になります。この時、1は平滑面を表すように因子が設定されているためだから、だそうです。(P.789記載)
正直ここら辺は調べても確信が持てないので、分かる人は教えてください。
では、実際に計算してみましょう。
L=100μm、l=1μm、D=2.5としたとき
cosθr=(L/l)D-2cosθ =(100/1)2.5-2=(100)0.5=10
このようにwenzel理論の一般的な想定よりもはるかに大きな値を得ることが出来ます。
フラクタル次元Dが大きいほど、濡れに対する効果も大きくなることが分かると思います。
それだけ、フラクタル表面が秘めるポテンシャルはすさまじいものだという事が、何となくお判りいただけましたでしょうか。
実際はそこまで単純ではないという話
ここまでの式ではwenzel理論を元に話を続けていたので、液体は微細凹凸表面の隙間に浸透し、完全に固体表面と接触していると仮定されます。
ですが、実際の親水撥水の表面での現象はここまで理論に沿っては動きません。
撥水材料であれば、毛細管現象によって完全に微細凹凸に浸透出来ず空気層が出来ることで、Cassie-Baxter理論と同様の状態になります。親水材料では、毛管凝縮によって空気中の液体が表面に吸着して水の膜を形成します。
このことから辻井らは、フラクタル表面の濡れの理論はWenzelとCassie-Baxter理論を統一したものであるとしています。実際の式はブログ文頭の論文より見れますので、良ければご覧ください。
暇があればここに追記します。
終わりに
長くなりなりましたが、フラクタル表面について少しだけでも理解してもらえましたでしょうか?
今回挙げたフラクタル表面の作成はアルキルケテンダイマーでの結晶凝集で作られていますが、モノマーの電解酸化重合[8]や、陽極酸化,ナノインプリント技術[9]までもが使われているそうです。
強度面の解決や実際の運用が今後どうなっていくのか、楽しみですね。
次は気分が乗れば接触角系で用いられる式や表面自由エネルギーの理論式でも解説します。
参考文献
文中に番号付きで記載していますので、ここでは書く上で参考になったものをいくつか置いておきます。
一般に記載するような発表年度や参考にしたページ数、著者などは面倒なので今回は省きます。ユルシテ
■アルキルケテンダイマー(AKD)サイズ剤におけるアルキル鎖の化学構造が 紙質と操業性に与える効果
https://www.jstage.jst.go.jp/article/jtappij/61/10/61_10_1170/_pdf/-char/ja
・アルキルケテンダイマーの結晶性について参考にした
■新合成サイズ剤アルキルケテンダイマ―について
https://www.jstage.jst.go.jp/article/jtappij1955/12/5/12_5_335/_pdf/-char/ja
・アルキルケテンダイマーの概要を知るために使用した
■フラクタルの表面科学への展開
https://www.jstage.jst.go.jp/article/oubutsu1932/64/8/64_8_788/_pdf
・上にも書いてはあるが、フラクタル表面の考えについてもう少し詳細かつ、何故アルキルケテンダイマーに出会えたかなどが書いてある。
■フラクタル表面構造と親水性・撥水性の物理
https://www.jstage.jst.go.jp/article/jvsj2/58/11/58_15-RV-028/_pdf
・辻井氏と共同研究していた恩田氏の論文。よりフラクタル表面について踏み込んだ考察を行っている。割と必読。
■協和界面化学のホームページ【界面科学の世界】
https://www.face-kyowa.co.jp/science.html
・界面科学のぬれ、表面張力をさらうならここでいいと思っている。因みに協和界面科学は接触角計などの界面科学の機械メーカーで、防曇性評価装置という、定量性に欠ける防曇を評価できるという他にない珍しい機械を販売している。
■親水性・撥水性の表面科学 ~超親水性・超撥水性と動的撥水性~
https://www.jstage.jst.go.jp/article/jvsj2/58/11/58_15-RV-027/_pdf
・超親水や超撥水について簡潔にまとまっている。参考文献の量がえぐいのでどちらかというとそれ目当てで見ていた節がある。
■超撥水表面
https://www.jstage.jst.go.jp/article/fiber/65/6/65_6_P_200/_pdf
・2009年に繊維学会誌に投稿されたもの。辻井らのアルキルケテンダイマーのみならず、Y. Sheenらのラズベリー状粒子など、超撥水についての技術を包括的に論じている。必読
■固体表面の濡れ性に対する表面粗さの効果
https://www.jstage.jst.go.jp/article/revpolarography/54/2/54_2_115/_pdf/-char/ja
・濡れモデルの支配因子について書いてあり、表面形状ごとの安定性について記載していたりとなかなか面白い。
■部材表面の濡れと難着雪技術の研究動向について
https://thesis.ceri.go.jp/db/files/17978299715af11136e817c.pdf
・難着雪技術と濡れに関係があったんだ…と知る機会になった論文。
また追記すると思います。
この記事が気に入ったらサポートをしてみませんか?
