
近刊『代数幾何学入門―代数学の基礎を出発点として―』まえがき公開
2021年1月下旬発行予定、『代数幾何学入門―代数学の基礎を出発点として―』(永井保成 著)のご紹介です。
同書のまえがきを、発行に先駆けて公開します。
***
『代数幾何学入門―代数学の基礎を出発点として―』はじめに
著:永井保成
本書は、早稲田大学基幹理工学部数学科3年次および4年次向けの講義「代数学C」で著者が扱ってきた話題についての講義予稿をもとにして作られたものである。代数学の必修講義で群、環、加群および体についての基礎的な事項を習得した数学科学部生に対して、代数幾何学のいくつかの話題を、代数学の基礎理論の延長上に置く形で提示し、代数幾何学への興味を喚起するとともに、可換環論、表現論、ホモロジー代数といったさらに進んだ純代数的な理論の学習を動機づけることを目指している。
代数学とは何であるか。それに極めて大雑把に答えるとすれば、「数と式の演算」について論じる数学の分野であるということができるだろう。日本の高校で教えられる数学に即していえば、数と式にまつわる代数的な議論の題材はもっぱら整数と1変数の多項式である。そのため、大学の数学において、高校数学に含まれる代数学の知識の延長線上で自然とその視野に入ってくるのは、おおよそ整数論と方程式論(Galois理論)だといってもあながち間違いではない。確かに、高校数学の座標幾何でおなじみの平面上の直線や円、あるいは二次曲線などは代数多様体の最も初歩的な例であるが、これらは代数的な手法というよりは、むしろ解析的な観点から扱われるウェイトが高いようにも感じられる。
そのような事情で、日本の高校を卒業し、日本の大学の数学科で学ぶ学部生にとってみれば、抽象代数学の初歩的話題の発展形としては、その問題意識のわかりやすさも手伝って、整数論は非常に自然で魅力的な課題に見えるだろう。それは、抽象代数学の発達の歴史的経緯からいっても当然である。一方、代数幾何学もまた抽象代数学の発展、とくに20世紀前半から中葉までの可換代数学の発展の最も主要な動機であったにもかかわらず、学生たちからするとどうも代数幾何学はとっつきにくいものであるらしい。それもそのはず、一部の学生たちの間には、代数幾何学を勉強するとなれば、まずは「アティマク」(Atiyah–MacDonaldのIntroduction to Commutative Algebra [2])を読んで、そののちに「ハーツホーン」(HartshorneのAlgebraic Geometry [10])を読破しなければならない、すべてはそれからだ、というような「神話」があるらしい。数学の才能にとくに恵まれた人物ならいざ知らず、私のように極めて平凡な頭脳しか持ち合わせていない者にとっては、この2冊を読みこなすことはかなりの重労働で、しかも、このコースに沿って勉強し続けたとして、500ページ近くある「ハーツホーン」のはじめの300ページぐらいを読み終えて初めて、言葉本来の意味での「幾何学」としての代数幾何に触れることができるのである。それまでは、代数学の議論と、それを用いた集合と位相(をうんと面倒くさくしたようなもの)のやり直しのような議論が延々と続き、1年、2年といった単位の時間それに耐えなければならない。*これはまさに「修行」の一種といわねばならない。このような状況は、代数的整数論の初歩の段階で「奇素数pが二つの平方数の和になるのは、pを4で割った余りが1になることと同値です、ではちょっと実験してみましょう」などとわかりやすい題材で楽しく勉強しながら誰でも容易に理論的構成の動機を得ることができるのとは対照的だと思われてならない。
*公正のため述べておくが、Hartshorneは極めて幾何学的な問題意識を常にもっていた代数幾何学者であり、[10]にも随所に幾何学的な例が散りばめられてはいる。しかし、たとえば私が学生のころを思い返すと、むしろ基礎付けの部分で必要とされる議論の正当化をぎっしりと詰め込んだ練習問題の重さばかりが目についたように思う。
著者は、「アティマク+ハーツホーン」のコースが、そればかりずっとやり続けるとすれば若干克己的なニュアンスを帯びるとはいえ、不必要に困難な修行であるとはまったく考えていない。今日の代数幾何学の興味深い問題のほとんどは、それらを意味がある形で提示するためだけにもハーツホーンレベルの基礎付けが必要とされるからだ。これは、どうやら代数幾何学の構造的な問題であるらしい。たとえば、代数幾何学の入門的な教科書が好んで取り上げる定理の一つとして平面曲線に対するBézoutの定理があるが、この定理の主張を厳密に述べようとすれば、射影平面曲線の定義や既約性などの基本的な性質が必要であるし、二つの平面曲線の交点における重複度を定義するために、結局のところ、何かの形で局所環とArtin環の理論を導入することになる。ことほどさように、代数幾何学の領域で遊ぶには、まずその基礎的なルールの習得にかなりの労力を割くことはある程度避けがたい面がある。代数幾何学の入門的教科書にも良書はたくさんあり、上に述べたBézoutの定理など、比較的易しく面白い定理をわかりやすく紹介してくれる。しかし一般的な傾向として、やはりその中で基礎付け・準備の占める割合はかなり高く、そこで与えられる基礎付けは、より発展的な学習・研究のためには不十分である場合が多い。前提知識を仮定せず、読みやすい教科書にしようとすればするほど、そこでそれなりの時間を費やすことになる基礎付けの部分は、後々になって本質的には同じ内容をより技術的に改良された形で文字どおり逐一やり直すことになる傾向がある。もちろん、この種の「やり直し」にはそれ自身価値があるともいえるが、学生時代の人生の時間は有限であるから、なるべくなら無駄な重複なく効率的に済ませてしまったほうがよいという考え方もあるだろう。それを極端に推し進めれば、とるものもとりあえず「アティマク+ハーツホーン」の関門を突破して、すべてはそれからということになるのであろう。
数学にとっての「基礎付け」というのは、音楽の練習でいえば、音階練習や発声練習のようなものである。楽器を上手に弾き、歌を上手に歌うためには音階練習や発声練習は欠かすことができないのであるが、しかし、これらの営為そのものは音楽というよりはむしろ単なる訓練に類するものであり、それ自身たとえば鑑賞の対象になるような音楽的魅力を有してはいないし、それどころか、やり方によっては極めて非音楽的な行為にもなりうる。数学でも同様に、基礎付けは、さまざまな数学の問題を理解し研究を行っていくために欠かすことのできないものであり、基礎付けにおける工夫というのもまた数学の重要な一側面をなしてはいるが、それ自身が数学の本来の最終目的、根本的な動機ではありえないのではないかと思われるのである。ピアノの習い始めだからといって、音階練習ばかり1年間も2年間もさせられて「曲」を弾かせてもらえなければ、どんな音楽好きであってもピアノの練習が嫌いになってしまうだろう。音楽を習い続けていくためには、それぞれのレベルで可能な音楽的な題材が常に必要なのである。その比喩でいえば、代数幾何学という分野の存在を知り、その入口に立っている学部生が、基礎的なトレーニングの傍ら、代数幾何学の面白さを知り、なぜさまざまの代数学的なテクニックが必要とされるのかを知るための「レパートリーブック」のようなものとして、著者は本書を企図したといえば伝わるだろうか。つまり、代数幾何学の分野ではどんな問題に興味がもたれ、どのような方法でそれらが解決されているのかについて、技術的な習熟を仮定せずになるべく「生きた」話題を提供しようと試みている。これはまた、私が担当した「代数学C」の講義の中心的な狙いでもあった。本書は、代数幾何初心者向けの「レパートリー」として、大まかにいって以下の三つのテーマを内包している。
I.平面曲線の特異点解消と形式的ベキ級数による代数多様体の局所理論
II.有限群の不変式と商特異点
III.ホモロジー代数の手法の可換代数学・代数幾何学への応用
そして、それぞれの話題について単線的に学ぼうと思えば、以下の順序で各講を読んでも理解できるように配慮している。
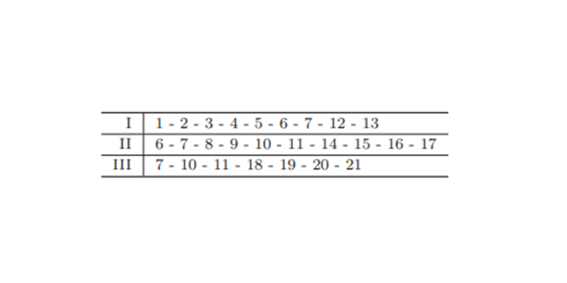
実際、著者はこれら三つのテーマそれぞれを題材にして半期1コマの講義を行ってきた。一方で、全体を通読しても違和感なく読み通せるはずである。また、これら三つのトピックは現代数学の文脈でいえば、可換代数学における局所環・次数環とそのホモロジー代数的扱いを基礎に展開されるものであり、その意味で一つの話題を取り扱っているといえる。専門家向けにいえば、この本はやや風変わりな代数幾何学風味の可換代数学の入門書だということになるだろう。
本文での解説は、学部レベルの代数学の基礎知識以外はなるべく自己充足的になるように努め、この本を手にとって読んでくれる読者に寄り添った丁寧な記述になるよう心がけた。各章末には若干の演習問題を用意した。基礎的な概念の理解を確かめるための簡単な問題もあるが、学部レベルの教科書としては労働量の多い実質的な問題も多く含まれている。本文の理解のために難易度の高い演習問題を解くことは必須ではないが、勇敢にもこれらの問題に取り組んだ読者には相応の見返りがあるだろう。代数学と幾何学の関連性について代数幾何学の立場から述べるにあたって避けることができないのが、Noether環および体上有限生成代数の次元論である。次元論自体一つの重要な可換環論のトピックであるが、本文中いくつかの場所で次元論の事実を用いるため、それに対する補足として、次元論の初歩的諸定理に対する最低限の解説を付録で与えた。紙幅の関係もあり、簡潔な叙述を与えることしかできなかったが、この部分はまさにスキーム理論を学ぶために必要とされる可換環論の知識であって、本書を付録も含めて消化すれば、いよいよ本格的な代数幾何学の勉強に踏み込んでいくことができるだろう。本書末尾にはさらなる探求のための読書案内を記した。本書を手に取った読者が、代数幾何学の面白さを発見し、より本格的な学習へと進まれることを願ってやまない。
永井保成(ながい・やすなり) 2005年東京大学大学院数理科学研究科博士課程修了。博士(数理科学)。
日本学術振興会特別研究員、韓国高等科学院研究員、マインツ大学数学研
究所研究員、東京大学大学院数理科学研究科特任助教を経て、2011年早
稲田大学理工学術院専任講師。その後、同准教授を経て、2017年より同
教授、現在に至る。
***
『代数幾何学入門―代数学の基礎を出発点として―』
https://www.morikita.co.jp/books/book/3421
著:永井保成
現代数学の華々しい分野として位置づけられている代数幾何学。しかし本格的に学ぼうとすると、膨大な量の理論を身に着ける必要があり、初学者が学習を進めていくのはハードルが高い分野でもあります。
本書は、学部レベルの代数学の知識だけを出発点として、代数幾何学を学ぶ入門書です。具体的な計算が数多く取り上げられており、幾何学的なイメージを膨らましながら読むことができます。また、代数幾何学で用いられる「代数学的なテクニック」がなぜ必要になるのかが懇切丁寧に説明されており、理論の流れが理解しやすいように配慮されています。
「『アティマク』や『ハーツホーン』を読まないと、代数幾何学は勉強できない」——そんな「神話」を覆す、画期的な入門書の誕生。
【目次】
第1講 平面曲線と特異点
1.1 平面曲線
1.2 平面曲線の特異点
第2講 形式的ベキ級数環
2.1 1変数形式的ベキ級数環
2.2 多変数の形式的ベキ級数環
2.3 平面曲線の接錐
第3講 ブローアップ
3.1 一般の体k上の平面曲線
3.2 射影直線
3.3 アフィン平面のブローアップ
3.4 全変換と狭義変換
3.5 ブローアップの繰り返し
第4講 Weierstrass多項式
4.1 平面曲線の摂動
4.2 Weierstrassの準備定理
4.3 形式的ベキ級数環のUFD性
第5講 平面曲線の特異点解消
5.1 最大接触度
5.2 平面曲線の特異点解消定理
第6講 アフィン代数多様体と座標環
6.1 アフィン代数多様体
6.2 座標環
6.3 接平面と特異点
第7講 加群
7.1 加群の定義
7.2 完全系列,5項補題とヘビ補題
7.3 Noether環とNoether加群
第8講 有限群の表現
8.1 有限群の表現
8.2 Maschkeの定理と既約分解
第9講 不変式環
9.1 不変量と不変式
9.2 有限群の表現から定まる不変式環
9.3 不変式環の有限生成性
第10講 次数加群とHilbert-Poincaré級数
10.1 次数加群
10.2 体上有限生成な次数環
10.3 Hilbert-Poincaré級数
第11講 テンソル積とHom加群
11.1 テンソル積
11.2 Hom加群
第12講 完備化
12.1 環の完備化
12.2 加群の完備化
12.3 Artin-Reesの補題
第13講 正則局所環
13.1 環の次元
13.2 正則局所環
13.3 アフィン代数多様体の非特異点の特徴付け
第14講 指標理論
14.1 有限巡回群の既約表現
14.2 Schurの補題
14.3 Hom表現
14.4 表現の指標
14.5 正則表現と群環
第15講 Molienの公式
15.1 対称式の環
15.2 Molienの公式
第16講 SL(2, C) の有限部分群
16.1 SL(2, C)とSU(2)
16.2 SU(2)とSO(3, R)
16.3 SO(3, R)の有限部分群
16.4 SU(2)の有限部分群
第17講 Klein-Du Val特異点
17.1 Klein-Du Val特異点
17.2 A型の場合
17.3 D型の場合
17.4 E_8型の場合
17.5 Klein-Du Val特異点の方程式と特異点解消
第18講 ホモロジー
18.1 複体のホモロジー
18.2 ホモロジー長完全列
第19講 加群の分解
19.1 射影分解
19.2 Tor加群
19.3 Tor長完全系列
第20講 二重複体
20.1 二重複体とその全複体
20.2 二重複体のTor加群への応用
第21講 Hilbertのsyzygy定理
21.1 次数付き極小自由分解
21.2 Tor加群との関係
21.3 Koszul複体
付録 A 局所化・整拡大
A.1 分数環・局所化
A.2 整拡大
A.3 整拡大の上昇定理と下降定理
付録 B Noether局所環の次元の理論
B.1 Artin局所環
B.2 Krullの単項イデアル定理
B.3 Krullの標高定理とパラメータ系
付録 C Noether正規化補題とHilbertの零点定理
C.1 体上有限生成代数と代数的独立性
C.2 Noetherの正規化補題
C.3 体上有限生成代数の次元論
文献案内 - あとがきにかえて
参考文献
索引
この記事が気に入ったらサポートをしてみませんか?

