
ABC185の解答
AtCoder Beginner Contest185を解き終わりましたので、私の解答をまとめていきます。
問題はこちらから。
難易度はこんな感じでした。
A:7(灰)
B:93(灰)
C:374(灰)
D:490(茶)
E:1468(水)
F:1053(緑)
Fが緑で少々驚きですね。結論としては「ライブラリを貼るだけ」なのですが、作問時にはそのライブラリ知識や使用法などの難易度がF相応であったと思われます。参加者のレベルが急激に上がっているってことでしょう。皆さんしっかりと勉強されています。私も負けないように頑張らねば。
それでは、解説を始めます。
A ABC Preparation
プログラミングコンテストを開催したいです。そのためには100,200,300,400点の問題がそれぞれ1つずつ必要なのです。現在、各問題の案をa1,a2,a3,a4ずつ持っています。さて、コンテストは最大で何回まで開催できるでしょう。
という問題です。
本問題では同じ案を繰り返し使うことができないそうです。ということで、今ある問題で実際にコンテストを開いてみます。
そうすると、a1,a2,a3,a4のなかで一番小さい数の問題案が真っ先に不足します。コンテストは4問構成なのでその時点で次回の開催はできなくなってしまいます。
ということで、問題の答えは、a1,a2,a3,a4の最小値となります。
実装です。
#include<bits/stdc++.h>
#define rep(i,n) for(int i =0;i<n;++i)
#define reps(i,s,n) for(int i =s;i<n;++i)
using namespace std;
using P = pair<int, int>;
using ll = long long;
int main()
{
int a1, a2, a3, a4;
cin >> a1 >> a2 >> a3 >> a4;
int ans = min({ a1,a2,a3,a4 });
cout << ans << endl;
return 0;
}min関数はmin(a1,a2)と2要素の比較となりますが、上記のように{ }で括って、リスト化することにより多要素の比較が簡単にできます。
でも、もしこれ以上要素が多くなったらおとなしく配列を使いましょう。
B Smartphone Addiction
最大容量 n のスマートフォンをもってお出かけします。現在、最大まで充電してます。お出かけ中は毎分1ずつ充電が減ってしまいます。また、途中で何度かカフェによります。カフェではコンセントが利用でき毎分 1 ずつ充電を回復できます。ただし、スマートフォンの最大容量以上には充電できません。さて、お出かけをして家に帰ってくるまでに充電が切れることがなかったかを判定してください。
という問題です。
まずは、制約を見てみましょう。
1 <= n <= 10^9
1 <= m <= 1000
1 <= t <= 10^9
(m : カフェに寄った回数 t : 家に帰った時刻)
です。m <= 1000ですので、
家→外→カフェ→外→カフェ→...→外→家
を一つずつ考えていっても計算が間に合いますね。そのため、愚直に書いてあげましょう。
カフェ i では、bi - ai だけ充電を回復して(nまで)、カフェ i から i+1に行く際には a(i+1) - bi だけ充電を消費します。
家からカフェ1に行く際と、カフェmから家に帰るまでに少し注意です。
実装です。
#include<bits/stdc++.h>
#define rep(i,n) for(int i =0;i<n;++i)
#define reps(i,s,n) for(int i =s;i<n;++i)
using namespace std;
using P = pair<int, int>;
using ll = long long;
int main()
{
ll n, m, t;
cin >> n >> m >> t;
ll mn = n;
vector<ll> a(m), b(m);
rep(i, m) cin >> a[i] >> b[i];
bool ok = true;
rep(i, m)
{
if (i == 0) n -= a[i];
else n -= a[i] - b[i - 1];
if (n <= 0) ok = false;
n += b[i] - a[i];
n = min(mn, n);
}
if (n - (t - b.back()) <= 0) ok = false;
if (ok) cout << "Yes" << endl;
else cout << "No" << endl;
return 0;
}上記の説明通りの実装になっています。
「注意です」と偉そうに書きましたが、私自身、本番は少し実装に悩みました。現在時刻を管理してあげてもよかったかもしれません。
C Duodecim Ferra
棒の分割方法を考えます。長さ l の棒を12分割します。このとき、分割後のそれぞれの長さは正整数となります。さて、分割の仕方は何通りありますか。
という問題です。
分割の区別が少しややこしいのですが、問題文の入力例2が13となるように、同じ長さの組であっても場所が変わるとそれらは区別されます。
こういう問題を見たときに、ぱっと解法が浮かばなくても「あーなんとなく、高校数学でやった記憶がふんわりあるわ」となった人は多いのではないでしょうか。
俗にいう「重複組み合わせ」ってやつですね。簡単のために数を減らして説明します。
問題
果物屋さんに行ったら、りんご、みかん、ぶどうがたくさん売っていました。あなたの袋には7個まで果物が入ります。さて、果物の買い方は何通りでしょうか。
今、適当に問題を考えました。これは、〇と|を使うと簡単に解くことができます。
7個の〇と2本の|にて、組み合わせは次図のように表現されます。
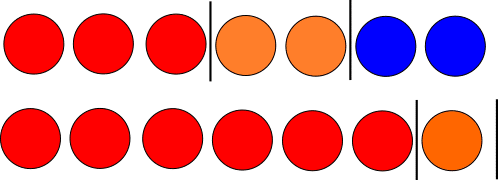
上 りんご:3、みかん:2、ぶどう:2
下 りんご:6、みかん:1、ぶどう:0
ですね。〇と|の位置をかえると全パターンが表現されます。そして、この組み合わせの数は
9C2 = 36
となります。
(〇と|が配置されるべき場所は7+2=9個。そのうち、|を置く場所を2つ選択する。上記例だと、上:4,7、下:7,9)
ただし、このままだと一個も買わない場合が発生します(図下:りんご6、みかん1、ぶどう0)。棒の分割問題では0は許されていないので、どうにかしましょう。
ということで、果物を選ぶ前にあらかじめ1つずつ買っておきましょう。
![]()

こうすれば、りんご2、みかん1、ぶどう4ですね。全部の果物を少なくとも1つ買うことができます。この場合の組み合わせの数は
6C2 = 15
です。総数から分割する数を引いてあげましょう。もっと言うと、買える果物の数-1です。
これで、果物の話はおしまいです。棒の話に戻りましょう。
こちらも果物と同様に考えると
(l-1) C 11
で答えが求まります。一発ですね。
さて、実装です。ここで注意なのが、問題文には「答えは2^64に収まる」という記述がありますが、計算過程での保障はされていないということです。そのためオーバーフローに気を付けましょう。
#include<bits/stdc++.h>
#define rep(i,n) for(int i =0;i<n;++i)
#define reps(i,s,n) for(int i =s;i<n;++i)
using namespace std;
using P = pair<int, int>;
using ll = long long;
ll comb(int n, int a)
{
ll r = 1;
rep(i, a)
{
r *= ((ll)n-i);
r /= ((ll)i+1);
}
return r;
}
int main()
{
int l;
cin >> l;
ll ans = comb(l-1, 11);
cout << ans << endl;
return 0;
}オーバーフローを防ぐために、「r*x」 と 「r/y」 をしていますが、この順番通りに処理を行うと「/y」の結果は必ず整数となり、切り捨て誤差が生じません。
その理由を簡単に、、、
割る数って「1,2,3,4,5,...」ってなりますよね。これが分母です。逆に分子は「n,n-1,n-2,n-3,...」です。まず、分母は1になります。1で割っても商は整数ですね。次に2です。2を割る前には分子には「n*(n-1)」がいます。こいつらは連続する2つの整数ですので、「(2*k)*(2*k-1)」もしくは「(2*k+1)*(2*k)」のいずれかです(kはnに対応する整数)。そのため、こいつらは素因数2を持つことが保証されます。同様の議論を3以降も続けていけば、答えには切り捨て誤差が含まれないことがわかります。
こんな感じです。ですので、割り算を先にやってはいけませんよ。
D Stamp
n マスが横方向に並んでいます。この中の m マスだけ青色で、あとは白色で塗られています。ここで、新しく赤色のスタンプを作ります。スタンプ幅は自分で決められます。このスタンプを用いて白色のマスを全部赤にしたいです。ただし、青色のマスを塗ること、マスからはみ出して塗ることは禁止です。さて、適切に幅を決めたとき、最小で何回スタンプを押せば、全部のマスが赤くなるでしょう。
という問題です。
この問題は2つの作業にわけることができます。
1.スタンプの幅を決める。
2.そのスタンプだと何手かかるか求める。
こんな感じで考えていきます。
まず1です。幅を決めましょう。
もちろん幅は大きいほうがいいです。大きければ大きいほど、一度に多くのマスを塗れます。ただし、余りにも大きすぎると青スタンプの隙間に入らなくなってしまって、全部のマスを塗れなくなります。
ということで、大きいほうがいいけど、青の隙間に入るいい感じの大きさが必要となります。
そのため、青スタンプが押されている間隔を調べていきましょう。このとき、左右の端のスタンプとマスの終端の隙間もお忘れなく。「0マス目とn+1マス目にも青スタンプがありますよ」と考えるとシンプルにまとめることができると思います。
これらの間隔の最小値がスタンプの幅となります。ただし、間隔が0のときはその間を赤で塗る必要はないので、1以上の最小値となります。
次に2.です。スタンプを押す回数を求めましょう。とはいいますが、1.にて全部の間隔を求めているので、それを使えば簡単です。例えば、スタンプ幅が2で間隔が8であれば、
8 / 2 = 4
ですね。間隔がスタンプ幅で割り切れないときは少し注意が必要で、間隔が3の時には
3 / 2 = 2 (切り上げ)
となります。これらの合計値が求める答えとなります。
実装です。
#include<bits/stdc++.h>
#define rep(i,n) for(int i =0;i<n;++i)
#define reps(i,s,n) for(int i =s;i<n;++i)
using namespace std;
using P = pair<int, int>;
using ll = long long;
const int inf = 1e9 + 5;
int main()
{
int n, m;
cin >> n >> m;
vector<int> a{ 0,n + 1 };
rep(i, m)
{
int ai; cin >> ai;
a.emplace_back(ai);
}
sort(a.begin(), a.end());
int mn = inf;
vector<int> d(m + 1);
rep(i, a.size()-1)
{
d[i] = a[i+1] - a[i] -1;
if (d[i] != 0) mn = min(mn, d[i]);
}
int ans = 0;
for (auto di : d)
{
ans += (di + mn - 1) / mn;
}
cout << ans << endl;
return 0;
}青色が0個の時もありますので、そういう場合も加味した実装をしてあげましょう。先にも述べましたが本実装では「0、n+1も青色で塗られてる」としました。
あとは切り上げ演算ですね。
(di + mn - 1) / mn
ちょこちょこと切り上げが要求される問題に出くわすので、式を覚えておくか、「そういえば簡単に切り上げられる書き方あったなー」と覚えておき、すぐに調べられるようになっておくと、役に立つと思います。
E Sequence Matching
長さ n の整数列 a と、長さ m の整数列 b があります。a,bからいくつか要素を取り除き、残ったものをそのままの順番でつなげて、a',b'を作ります。このとき、a'とb'の長さが等しくなるような取り方をします。a,bから取り除いた要素の合計数を x 、a'i ≠ b'i を満たす i の数を y としたとき、x+yの最小値はいくつでしょう。
という問題です。
どうやって解こうか悩んでいたところ、非常にわかりやすく解説をしてくださっている動画がありましたので、紹介します。
本記事のE解説もこの動画を参考にしながら書いていきます。ご了承ください。
まず「要素を消す」や「要素が不一致」だと考えにくいので、問題文を読み替えていきます。
どんな入力a,bからでも作成が可能で、 y = 0、つまり要素の不一致が存在しない整数列 z ってどのような整数列でしょうか。a,bともにこの整数列 z になるまでに消した要素の個数さえ求めてしまえば、その値が答えになると思いませんか?
この整数列 z は長さが 0 で空っぽの整数列となります。要素が一つもないので、要素の不一致は発生しないし、要素を全部消せばよいのでどんな入力からも作ることが可能です。
ということで、入力a,bを頭から消していって全部消すまでに何回消したかをカウントしていきましょう。これで「要素を消す」の操作(xの操作)を行うことができました。
操作はもう一つあります。「要素の不一致」ですね。
これは、要素が「不一致」であれば、ペナルティー"+1"で「一致」していればペナルティー"0"と言い換えることができます。ペナルティーがないということは、その数字をもともと存在しなかったものとして扱うことができるということです。無視しましょう。
上記の消す操作と対応させましょう。a,bともに先頭から1文字ずつ消していくのですが、a,bの先頭の文字が一致していたら、消すカウントを増やすことなく2文字を消去することができます。
さらに言うのであれば、もし不一致の場合でもペナルティーの1を払うことでa, b の2文字を消すことができるので、普通に消すよりもこっちの方がお得です。
以上により、
要素を消す:消した数を数える
要素の不一致:もし一致していたら数を増やさず消せる。不一致なら+1することで、a,bから一文字ずつ消すことができる。
という、整数列を消した数をカウントしながら消す問題に読み替えることができました。
あとは、この問題をdpにて解いてあげましょう。設計はこうです。
dp[i][j] : aからi文字、bからj文字消した時の消した回数
ぱっと見ると、「消した回数ってi+jじゃん」ってなりそうですが、要素が一致していたら、回数を増やさず i, j だけ増やすことができます。ここが問題の肝なのでしょう。
実装の前に入力例1を使って遷移を図で示します。少しでもイメージをつかんでいただけると嬉しいです。

スタートからゴールに至るまでに獲得得点?の少なくなる経路を選びましょう。その最小値が答えです。
実装です。
#include<bits/stdc++.h>
#define rep(i,n) for(int i =0;i<n;++i)
#define reps(i,s,n) for(int i =s;i<n;++i)
using namespace std;
using P = pair<int, int>;
using ll = long long;
const int inf = 1e9;
void chmin(int& a, int b) { a = min(a, b); }
int main()
{
int n, m;
cin >> n >> m;
vector<int> a(n);
vector<int> b(m);
rep(i, n) cin >> a[i];
rep(i, m) cin >> b[i];
vector<vector<int>> dp(n+1, vector<int>(m+1,inf));
dp[0][0] = 0;
rep(i, n+1)rep(j, m+1)
{
if(i < n) chmin(dp[i + 1][j], dp[i][j]+1);
if(j < m) chmin(dp[i][j+1], dp[i][j]+1);
if (i < n && j < m)
{
if (a[i] == b[j]) chmin(dp[i + 1][j + 1], dp[i][j]);
else chmin(dp[i + 1][j + 1], dp[i][j] + 1);
}
}
cout << dp[n][m] << endl;
return 0;
}i = n またはj = mの場合でも遷移が可能な点に注意しましょう。これを忘れると、i=n, j=mへの遷移がi=n-1, j=m-1からしか起こりえなくなります。
F Range Xor Query
整数が n 個与えられます。その後xorに関する2種類のクエリがいっぱい飛んできます。
1 : x番目の数 ax を ax xor yに置き換える。
2 : ax xor a(x+1) xor ... xor ayを出力(x<=y)
これらを適切に処理しましょう。
という問題です。
本問題に関しては、
Segment Treeをxorに拡張すれば答えが求まる
でおしまいです。
ただ、それだと私的に面白くないのでFenwick Tree(Binary Indexed Tree : BIT)における解答を書いてきます。ただし、C++でも時間が厳しかったので、他言語だと難しいかもしれません。また、Segment Treeによって解いた実装も最後の方にちょこっと載せておきます。
まず、BITとSegment Treeってなんだ?ということで、そちらの解説記事を載せておきます。
では、BITをもちいた解法を書いていきます。
まず、xorってなかなか面白い演算でして以下の論理式に従います。
0 0 → 0
0 1 → 1
1 0 → 1
1 1 → 0
入力が同じなら「0」、異なるなら「1」を出力してくれます。こいつは日常生活でも実は大活躍しています。例えば階段の電気です。上と下のスイッチがありますが、どちらを押してもオン、オフが切り替わりますよね。あの仕組みの正体はこいつです。すごいやつです。
さて、もうちょっと拡張しましょう。3入力です。
0 0 0 → 0
0 0 1 → 1
0 1 0 → 1
0 1 1 → 0
1 0 0 → 1
1 0 1 → 0
1 1 0 → 0
1 1 1 → 1
こうですね。2入力ずつ行えばこうなることがわかると思います。
この表およびスイッチの切り替えからもわかる通り、実はxor演算って1の数の偶数、奇数により判定が行われています。今回はこの性質を用いて問題を解きます。
少し問題に戻ります。この問題は「要素をxorした結果に書き換える」と「x~yの値のxor」の2つから構成されるのですが、愚直にやればどちらも簡単に求めることができます。ただし、2つ目の「x~yの値のxor」にとっても時間をかかることを対処する必要があります。
この点に対してBITとxorの性質を用いてアプローチをかけるのが今回の解法です。
入力例1を例にとります。
1 2 3ですね。これらをまず2進数表記します。
1 : 0 1
2 : 1 0
3 : 1 1
ですね。1~3のxorを取りましょう。このとき、各桁はそれぞれ独立に扱うことができます。ここ大事です。
1 : 0 1
2 : 1 0
3 : 1 1
sum : 2 2
xor : 0 0
ということで、答えは0です。sumの偶奇でxorの判定ができます。次に2~3で行うと、
2 : 1 0
3 : 1 1
sum : 2 1
xor : 0 1
で答えは1ですね。区間和を高速に取得することができれば、この手法で「x~yの値のxor」のクエリが処理できそうです。
ということで、ここでBITを用います。詳しくは別記事で書いていますのでそちらをご覧いただけるとありがたいです。
まず、桁数分のBITを用意します。制約より30桁分用意すれば十分です(上の場合ですと2個のBITを用意すれば十分ですが、入力の最大値は与えられないため、最大ケースの30桁分用意しておくと実装が簡単です)。
次に、各数字、各桁において「1」がたっていたら該当する場所に「1」を加算します。
あとは「x~y」の区間においてそれぞれの桁の1の数の数を求めて、その偶奇から、xor演算をしてあげましょう。xorの結果を10進数に戻すことを忘れないように。
これで「x~yの値のxor」のクエリができました。
次に「要素をxorした結果に書き換える」を考えていきます。
axとyのxorをするのですが、ここで必要なのは「xorの結果、axの各桁のビットが反転するか、そのままか」という情報だけです。
ということで、yを2進数表記してあげて、yの該当桁が0ならそのまま、1であれば、ビット反転(0なら1、1なら0)にしてあげましょう。これだけで「要素の書き換え」はおしまいです。
以上により、2種のクエリの処理ができました。
実装です。
#include<bits/stdc++.h>
#define rep(i,n) for(int i =0;i<n;++i)
#define reps(i,s,n) for(int i =s;i<n;++i)
using namespace std;
using P = pair<int, int>;
using ll = long long;
//0-indexed
template<typename T>
struct BIT {
int n;
vector<T> bit;
BIT(int n = 0) :n(n), bit(n + 1) {}
void add(int i, T x = 1) {
for (i++; i <= n; i += i & -i) {
bit[i] += x;
}
}
T sum(int i) {
T x = 0;
for (i++; i; i -= i & -i) {
x += bit[i];
}
return x;
}
};
int main()
{
int n,q;
cin >> n >> q;
vector<int> a(n);
vector<BIT<int>> b;
rep(i, 30) b.emplace_back(n);
rep(i, n)
{
cin >> a[i];
int ta = a[i];
int cnt = 0;
while (ta>0)
{
if (ta % 2 == 1) b[cnt].add(i,1);
ta /= 2;
++cnt;
}
}
rep(i, q)
{
int t, x, y;
cin >> t >> x >> y;
--t;
if (t == 0)
{
--x;
int ta = a[x];
int na = 0;
int cnt = 0;
while (ta > 0 || y > 0)
{
int tai = ta % 2;
if (y % 2 == 0) na += tai << cnt;
else
{
na += !tai << cnt;
b[cnt].add(x,tai == 0 ? 1:-1);
}
ta /= 2;
y /= 2;
++cnt;
}
a[x] = na;
}
else
{
--x; --y;
int sum = 0;
rep(j, 30)
{
int ts = b[j].sum(y) - b[j].sum(x-1);
sum += (ts % 2) << j;
}
printf("%d\n", sum);
}
}
return 0;
}最大桁数が30ですので何とかなりました。これを定数倍と呼んでいいのかはわかりません。
ここまでがBITによる実装です。
segment treeによる解法でも解きましたので併せて載せておきます。
#include<bits/stdc++.h>
#define rep(i,n) for(int i =0;i<n;++i)
#define reps(i,s,n) for(int i =s;i<n;++i)
using namespace std;
using P = pair<int, int>;
using ll = long long;
//0-indexed
template<class T, T (*op)(T,T), T(*e)()>
class segtree
{
private:
int n;
vector<T> v;
public:
segtree(int n_)
{
int x = 1;
while (n_ > x) x <<= 1;
n = x;
v.resize(2 * n - 1, e());
}
void set(int k, T x)
{
k += n - 1;
v[k] = x;
while (k > 0)
{
k = (k - 1) / 2;
v[k] = op(v[k*2+1],v[k*2+2]);
}
}
T get(int k) { return v[k + n - 1]; }
//[a,b)
T query(int a, int b) { return query_sub(a, b, 0, 0, n); }
T query_sub(int a, int b, int k, int l, int r) {
if (b <= l || r <= a) return e();
if (a <= l && r <= b) return v[k];
T c1 = query_sub(a, b, 2 * k + 1, l, (l + r) / 2);
T c2 = query_sub(a, b, 2 * k + 2, (l + r) / 2, r);
return op(c1,c2);
}
//display segtree value
void display(string text = "segtree value")
{
cout << text << endl;
int cnt = 0;
int end = 1 << cnt;
int l = v.size();
for (int i = 0; i < l; ++i)
{
cout << v[i] << " ";
if (i == end - 1)
{
++cnt;
end += 1<<cnt;
cout << endl;
}
}
cout << endl;
}
};
int op(int a, int b) { return a ^ b; }
int e() { return 0; }
int main()
{
int n,q;
cin >> n >> q;
segtree<int,op,e> sg(n);
rep(i, n)
{
int ai; cin >> ai;
sg.set(i,ai);
}
rep(i, q)
{
int t, x, y;
cin >> t >> x >> y;
--x;
if (t == 1) sg.set(x, op(sg.get(x), y));
else printf("%d\n", sg.query(x,y));
}
return 0;
}抽象化したsegment treeに
演算
int op(int a, int b) { return a ^ b; }
単位元
int e() { return 0; }
を与えています。確実にこちらの方がスマートですね。segment treeを使えるようにしましょう。
今回は学びの多い回でした。ライブラリを手足のように使えるようにして、次はコンテスト中に正解したいものです。
