
ABC184の解答
AtCoder Beginner Contest184が解き終わったので解答を書いていきます。
問題はこちらから。
難易度はこんな感じでした。
A 6(灰)
B 20(灰)
C 782(茶)
D 1276(水)
E 1418(水)
F 1423(水)
なかなか面白い難易度構成になってますね。解く問題を適切に選択できたかどうかが、成績に関わっているのではないのでしょうか?時間内に処理できる問題を見極めていきましょう。
ただ、テスト後はしっかりと全部復習しましょう。
ではいきます。
A Determinant
2*2行列の行列式は?
という問題です。行列式は
a*d - b*c
と与えてくれています。制約も緩いので、これに代入をしておしまいです。
#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define reps(i,s,n) for(int i=s;i<n;++i)
using ll = long long;
using namespace std;
using P = pair<int, int>;
int main()
{
int a, b, c, d;
cin >> a >> b >> c >> d;
cout << a * d - b * c << endl;
return 0;
}前回のA問題はReLUで今回は行列式と、なんか大学の物理、数学でよく聞くような単語がテーマになってますね。次あたりにxorの論理式とかでないですかね?
B Quizzes
n 問のクイズに答えます。はじめ x 点もっており正解なら+1、不正解なら-1されます。ただし、0より小さくなりません。さて、最終的な得点はいくつでしょう。
という問題です。
制約は
1 <= n <= 2*10^5
ですので、愚直にやりましょう。
正解なら+1
不正解なら-1(ただし持ち点が0のときはそのまま)
これで完了です。
#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define reps(i,s,n) for(int i=s;i<n;++i)
using ll = long long;
using namespace std;
using P = pair<int, int>;
int main()
{
int n, x;
string s;
cin >> n >> x >> s;
int ans = x;
rep(i, n)
{
char c = s[i];
if (c == 'o') ++ans;
else ans = max(ans - 1, 0);
}
cout << ans << endl;
return 0;
}0点にて不正解の処理をなんかうまく書きましょう。maxでもいいですし、ifでもいいですし、なんかうまくやりましょう。
C Super Ryuma
無限に広がる二次元平面上に「超竜馬」という将棋の駒があります。この駒の動きは以下の図の通りです。この駒が、始点(c1,r1)から終点(c2,r2)まで行くためには何手必要ですか?
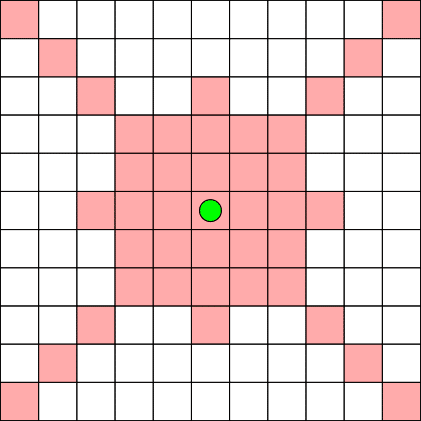
という問題です。
色々と考えようがある問題だと思います。可能な限りシンプルな方法で解いていきます。
これからいろいろと考えていくのですが、そのたびに
「始点が終点の右上にあるからー、こんどは左下にある場合ー」
って考えるのは大変なので、まずは、終点を第一象限にまとめてしまいます。幸いなことに盤面は無限遠であり、駒の動きが上下左右対称です。
始点を(0, 0)に移動して終点もそれに伴って動かします。
具体的には
c2 -= c1
r2 -=r1
c1 = 0
r1 = 0
こうです。そして、c2とr2の符号を正にします(x=0とy=0軸対称)。これ以降、説明のためにc2 = gx, r2 = gyとします。
これで第一象限のみを考えればよくなりました。少し楽になりますね。
これから必要な手数を数えていきます。
実を言うと?当たり前ですが?必要な手数は0 ~ 3手のいずれかとなります。
2回斜めに移動すれば大体の場所に行けます。が、将棋の角が目の前のマスに行けないように、斜め移動だけではどうしてもいけない場所が存在します。そういう時は2回+近くに移動の3回となるわけです。
ということで、必要な手数が0 or 1 or 2 or 3を判定しましょう。
0手のとき
gx = gy = 0のときです。簡単ですね。
1手のとき
まず、駒の移動を2つに分けます。
a:近くに移動(マンハッタン距離が3以下。縦横に3回の移動で行ける。)
b:斜めに移動(x = yとなる点に移動)
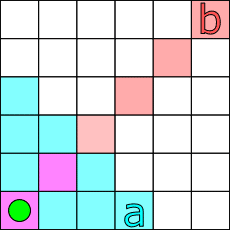
a,bの移動をどちらかの片方でも満たしていれば良いので、それを確認しましょう。
a:gx +gy <= 3
b:gx = gy
さて、これで半分終わりました。もうちょっと頑張りましょう。
2手のとき
ここが山場です。
まず、移動方法としては3通り考えられます。前述のa,b移動を用いると、
c:a移動2回
d:b移動2回
e:a移動1回とb移動1回
ですね。一つずつ見ていきます。
c:aはマンハッタン距離3だけ移動できますので、2回ですと6まで移動できます。したがって、
gx + gy <= 6
で判定できます。
e : b を2回用いるとどんな場所にも移動できそうですが、前述のとおりどうしても移動できない場所が存在します。これは、斜め移動はマンハッタン距離を±2する移動ということが原因です。例えば、正面のマスはマンハッタン距離が1ですので、どんなに頑張っても斜めだけではたどり着けません。
ということで、bを2回で行ける場所というのは、マンハッタン距離が偶数の場所です。判定は
(gx + gy) が偶数
でよいでしょう。
f : a, bを一回ずつ使います。どちらの移動を先に行っても良いのですが今回はb -> aとしましょう。まず、bの移動では x = y の好きなところに行けます。その後、a 移動ができますので、x = yの点からマンハッタン距離3以下の座標に到達することができます。判定としては、
abs(gx - gy) <= 3
ですね。この移動のイメージとしては、マンハッタン距離が偶数の場所はb移動2回ではいけないけど、もしも、その座標がx = y の近くにあればb -> aで何とかなるよ、っていう感じですかね。
これで、2手移動は完了です。
3手のとき
それ以外です。おしまい。
さて、最後に移動に何手かかるかを図で示します。この図と対応させると、上記の説明が理解しやすくなるかなと思います。

ようやく実装です。
#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
using namespace std;
using P = pair<int, int>;
using ll = long long;
int main()
{
int i1, j1, i2, j2;
cin >> i1 >> j1 >> i2 >> j2;
i2 -= i1;
j2 -= j1;
i1 = 0;
j1 = 0;
i2 = abs(i2);
j2 = abs(j2);
if (i2 == 0 && j2 == 0)
{
cout << 0 << endl;
return 0;
}
if (i2 + j2 <= 3 || i2 == j2)
{
cout << 1 << endl;
return 0;
}
if (i2 + j2 <= 6 || (i2 + j2) % 2 == 0 || abs(i2 - j2) <= 3)
{
cout << 2 << endl;
return 0;
}
cout << 3 << endl;
return 0;
}考察は長かったですが、実装はシンプルですね。
ただ、試験中にここまで綺麗に問題を整理できる場合ばかりでもないかと思います。私は色々と試行錯誤を重ねて泥臭くもacしました。ということで、コンテスト中のプログラムも載せておきます。試験中はacした人の勝ちなので、どんな形であれ諦めずに頑張りましょう。
#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define reps(i,s,n) for(int i=s;i<n;++i)
using ll = long long;
using namespace std;
using P = pair<int, int>;
int x[4] = { 0,0,-3, 3 };
int y[4] = { 3,-3,0,0 };
int main()
{
int r1, r2, c1, c2;
cin >> r1 >> c1 >> r2 >> c2;
int dx = r1 - r2;
int dy = c1 - c2;
bool ok = false;
if (dx == 0 && dy == 0)
{
cout << 0 << endl;
return 0;
}
if (abs(dx) + abs(dy) <= 3) ok = true;
if (abs(dx) == abs(dy)) ok = true;
if (ok)
{
cout << 1 << endl;
return 0;
}
vector<int> col1x, col1y,col2x,col2y;
rep(i, 5)
{
rep(j, 5)
{
col1x.emplace_back(r1 - i - 2);
col1y.emplace_back(c1 - j - 2);
col2x.emplace_back(r2 - i - 2);
col2y.emplace_back(c2 - j - 2);
}
}
rep(i, 4)
{
col1x.emplace_back(r1 + x[i]);
col1y.emplace_back(c1 + y[i]);
col2x.emplace_back(r2 + x[i]);
col2y.emplace_back(c2 + y[i]);
}
rep(i, col1x.size())
{
rep(j, col1x.size())
{
if (col1x[i] == col2x[j] && col1y[i] == col2y[j]) ok = true;
}
}
int rel = 0;
int jx;
int jy;
if (dx > 0) jx = r1 - abs(dx);
else jx = r1 + abs(dx);
if (dy > 0) jy = c1 - abs(dx);
else jy = abs(dx);
if (c2 - 4 <= jy && jy <= c2 + 4) ok = true;
if ((abs(dx) + abs(dy)) % 2 == 0) ok = true;
if (ok)
{
cout << 2 << endl;
return 0;
}
else
{
cout << 3 << endl;
return 0;
}
}D increment of coins
袋の中に「金、銀、銅」の3種類の硬貨がそれぞれa, b, c枚入っています。いずれかの硬貨が100枚になるまで次の操作を繰り返します。
「ランダムに袋から硬貨を取り出し、同じ硬貨を2枚戻す」
このときの、操作回数の期待値を求めましょう。
という問題です。
このまま考えてもイメージがしにくいので、もうちょっと簡単にしてみます。10枚たまったら終了としましょう。そして、初期値は「9, 9, 8」とします。この状態から終了までの遷移を図で示すと次のようになります。
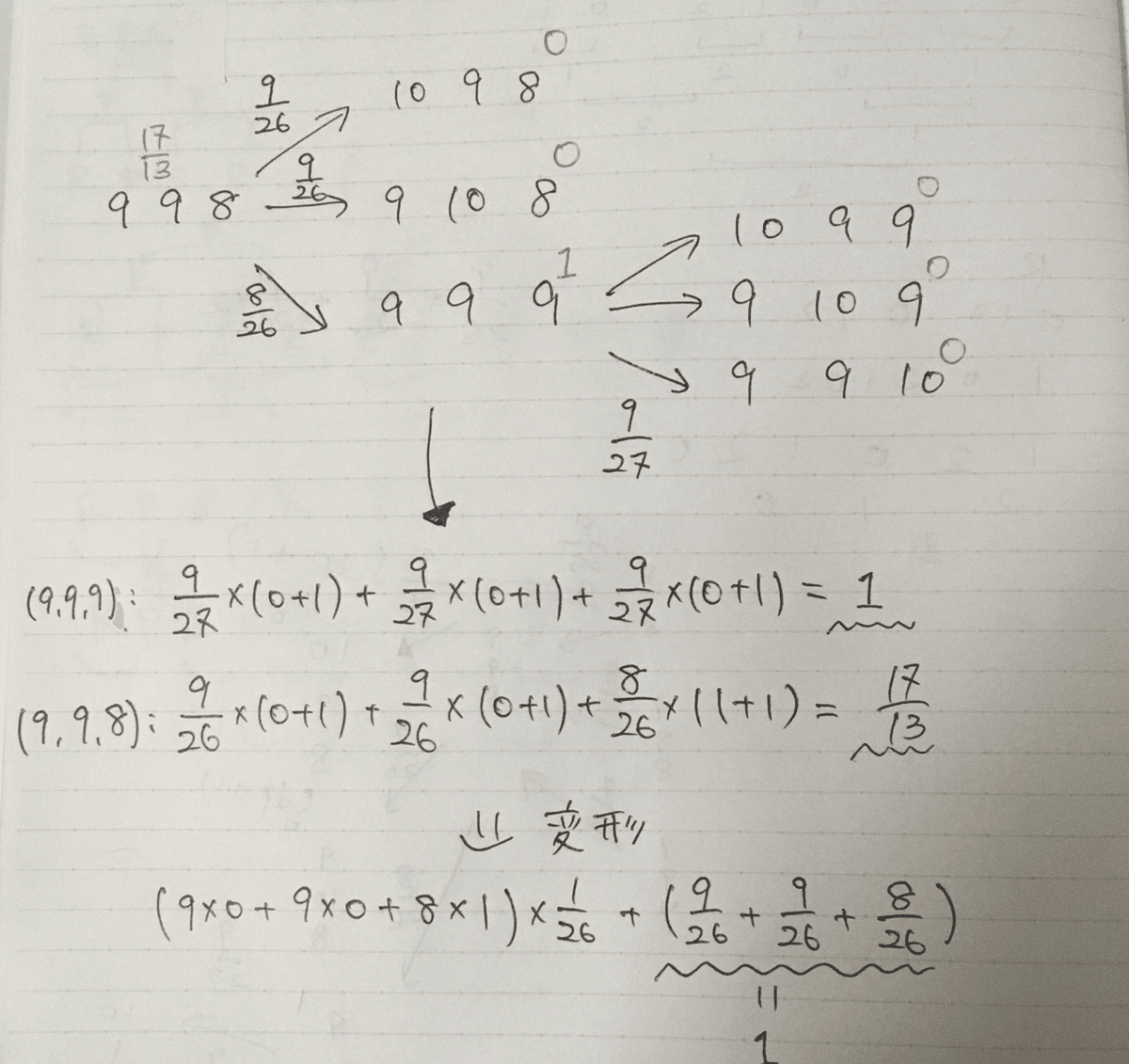
赤い数字はその状態における、終了までの操作回数の期待値です。10があるものは操作終了なので、0ですね。「9,9,9」の場合はどれを選んでも終了なので、操作回数は1となります。
次にこの 「1」 をどうやって求めたかを考えます。
「9,9,9」からは次の3つの状態に遷移することが可能です。
金貨を選ぶ→確率9/27で「10,9,9」となる。
銀貨を選ぶ→確率9/27で「9,10,9」となる。
銅貨を選ぶ→確率9/27で「9,9,10」となる。
遷移後の状態においては、既に「10」があるので操作回数の期待値は 0 となります。
ということで、「9,9,9」の矢印を逆向きにたどってあげましょう。遷移確率と遷移後の期待値により「1」を求めることができました (図中段)。
同様にして、「9,9,8」も求めることが可能です。
ということで、動的計画法dpにて目的の期待値を求めてあげましょう。
dp[i][j][k] : 金貨 i 枚, 銀貨 j 枚, 銅貨 k 枚のときの操作の期待値
金、銀、銅のいずれかが100の状態から、硬貨の数を減らすようにその期待値を更新してきます。更新式は図下段の変形した式をi,j,kで一般化したものになります。
dp[i][j][k]
= (dp[i+1][j][k] * i + dp[i][j+1][k] * j + dp[i][j][k+1] * k) / (i+j+k) + 1
あとは、0除算に気を付けましょう。
実装です。
#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
using namespace std;
using P = pair<int, int>;
const int MAX = 100;
double dp[MAX+1][MAX+1][MAX+1];
int main()
{
int a, b, c;
cin >> a >> b >> c;
for (int i = MAX - 1; i >= 0; --i)
{
for (int j = MAX - 1; j >= 0; --j)
{
for (int k = MAX - 1; k >= 0; --k)
{
if (i + j + k == 0) continue;
dp[i][j][k] += dp[i + 1][j][k] * i;
dp[i][j][k] += dp[i][j + 1][k] * j;
dp[i][j][k] += dp[i][j][k + 1] * k;
dp[i][j][k] /= ((double)i + j + k);
dp[i][j][k] += 1;
}
}
}
printf("%.10f\n", dp[a][b][c]);
return 0;
}解説を見たときに「なんで+1をするのか?」がいまいちわかってませんでした。でも、自分で式を変形してみたら、ひょこっと出てきました。そういうことだったんですね。
E Third Avenue
h * wの盤面があり、盤面にはそれぞれ、道(".")、岩("#")、スタート("S")、ゴール("G")と各種アルファベット("a~z")が書いてあります。この状態において、スタートからゴールまで移動します。可能な行動は以下の通りです。
上下左右の岩じゃないマスに移動(1秒)
現在のマスと同じアルファベットの書かれたマスにワープ(1秒)
さて、スタートからゴールまでの最短時間はいくつでしょう。
という問題です。
この問題は幅優先探索により答えを求めることができます。ということで、まずは簡単に幅優先探索を説明します。ひとまず、ワープ話の方向で進めます。
幅優先探索は次の図のように近くから一つずつ探索をしていくアルゴリズムです。まず、始点から距離が1の場所を確定させます。次に2の場所、3の場所、...といった感じです。こうすることで最短距離は8と求まりました。とっても簡単ですね。
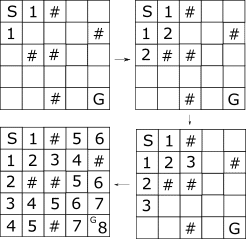
ここで大切なのは、2が確定する前に3を探索しないことです。「近くから」というルールを絶対に破ってはいけません。言葉をかえるとすれば「数字の小さい場所から探索、コストの更新は発生しない」ですかね(厳密でなかったらすみません)。これは、本問題を解く際に非常に大切な要素となります。
そのため、幅優先探索は「移動に要するコストが等しい」という条件を満たす問題にのみ用いることができます。コストが違う場合には、少し工夫をするか、別のアルゴリズムを調べましょう。
幸いなことに本問題はすべてのコストが「1」ですので、本手法で解くことが可能です。ワープを含めた図を見てみましょう。同じ色にワープできます。

ですかね。ということで6手で着きました。
さて、実装だ、といきたいのですが、このまま実装すると計算時間が間に合いません。ここまで、偉そうに書いてきましたが、どうやらダメみたいです。
どうしてダメかを説明していきます。
幅優先探索の実装にはqueueという構造を用います。queueはいわゆる「先れ先出し」のデータ構造です。上の図の環境を例にして動作を見ていきましょう。
まず、開始点(0, 0)をqueueに入力します。
queue{} <- (0,0)
入力が終了しましたら先頭の要素を取り出します。
(0,0)<- queue{}
(0, 0)から移動可能な点の座標をqueueに入力しましょう。
queue{}<-(1,0), (0,1)
先頭の(1,0)を取り出して探索し、次の探索点を入力します。ということを続けます。このとき、探索済みの場所は入力しません。
(1,0)<-queue{(0,1)}<-(2,0), (1,1)
(0,1)<-queue{(2,0), (1,1)}<-
(2,0)<-queue{(1,1)}<-(3,0)
さて、次は(1,1)のワープです。ですが今までと同じで大丈夫です。
(1,1)<-queue{(3,0)}<-(0,3),(1,2),(3,2)
これを探索点がなくなるまで、つまりqueueが空っぽになるまで行います。
ここまで動作を見てきました。さて、上記の処理において、盤面における数字が小さい順に処理されていることに気づいたでしょうか?
「先入れ先出し」を徹底すると、幅優先探索が実現されるのです。
本題に戻します。どうして時間切れになってしまうかです。
今回、緑のワープは3か所ありますが、(1,1)からワープをした際には、残りの2箇所(0,3), (3,2)がqueueに入力されます。そして、それらが取り出されたとき((0,3)を取り出してみる)には、それ以外の2箇所((1,1), (3,2))の探索を行います。
つまり、計算オーダーが同一ワープの数の2乗程度になります。
盤面が小さければまだ良いのですが、2000*2000の盤面がスタートとゴール以外全部、緑、となったら大変な気がしてきませんか。
以上が計算が間に合わない理由です。
じゃあ、どうするのかといいますと、一度ワープした色において、再びワープすることを禁止しましょう。そうすれば、計算オーダーは線形(1乗)になります。
私はここで、
「ワープを禁止してしまったら、もしも禁止後に今までよりも優れた経路でワープ地点まで行けた場合に、値が更新できないじゃないか」
という疑問を持ちました。日本語が怪しいですがなんとなく伝わるでしょうか。
ただし、この疑問はそもそもが間違っていました。先にも述べましたが幅優先探索では「近くから」「値が小さいものから」がとっても大切です。このルールに則る限り「さらに良い経路」なんてものは存在しないのです。
さて、ここまで長く書いてきましたが実装に移ります。
#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
using namespace std;
using P = pair<int, int>;
char g[2005][2005];
int dist[2005][2005];
int dj[] = { 0,0,1,-1 };
int di[] = { 1,-1,0,0 };
const int inf = 1e9;
int c2i(char c)
{
return c - 'a';
};
int main()
{
int h, w;
cin >> h >> w;
vector<vector<P>> warp(26);
//すべてのマスのコストを無限にしておく
rep(i, h)rep(j, w) dist[i][j] = inf;
int si, sj, gi, gj;
rep(i, h)rep(j, w)
{
char c;
cin >> c;
if (c == 'S')
{
si = i;
sj = j;
g[i][j] = '.';
dist[i][j] = 0;
continue;
}
else if (c == 'G')
{
gi = i;
gj = j;
g[i][j] = '.';
continue;
}
//ワープ地点のある座標をアルファベットごとに取得。
if (c != '.' && c != '#') warp[c2i(c)].emplace_back(i, j);
g[i][j] = c;
}
queue<P> q;
q.emplace(si, sj);
while (!q.empty())
{
P p = q.front();
int ti = p.first;
int tj = p.second;
q.pop();
//上下左右
rep(i, 4)
{
int ni = ti + di[i];
int nj = tj + dj[i];
if (nj < 0 || w - 1 < nj) continue;
if (ni < 0 || h - 1 < ni) continue;
if (g[ni][nj] == '#') continue;
//コストが小さければ書き込む(未探索)
if (dist[ti][tj] + 1 >= dist[ni][nj]) continue;
dist[ni][nj] = dist[ti][tj] + 1;
q.emplace(ni, nj);
}
//ワープ移動
char c = g[ti][tj];
if (c != '.' && c != '#')
{
auto pv = warp[c2i(c)];
for (auto p : pv)
{
int ni = p.first;
int nj = p.second;
if (dist[ti][tj] + 1 >= dist[ni][nj]) continue;
dist[ni][nj] = dist[ti][tj] + 1;
q.emplace(ni,nj);
}
//一度ワープしたら、ワープ地点の情報を削除する。
//ワープ禁止
warp[c2i(c)].clear();
}
}
int ans = dist[gi][gj];
if (ans == inf) ans = -1;
cout << ans << endl;
return 0;
}私は本問題を通して経路探索について少しだけ詳しくなれました。まだまだ、ふわっとしている部分はありますが、こればっかしは問題を解くしかないのでしょう。類題?として、abc176dに「コスト 0or1の幅優先探索」がありますので、そちらを解いてみるのも良いかと思います。
F Programming Contest
解くのに ai 分かかる問題が n 問あります。0問以上を選んで、その時間の総和が t 以下となるように問題を解きます。このときの時間の総和の最大値を求めよ。
という問題です。
比較的シンプルな問題ですね。なんといっても題名がとってもシンプルですね。そのままといいますか。
愚直にやればとっても簡単です。全パターン試しましょう。n 問に対して、i 問目を選ぶ、選ばないとしてあげれば、2^nで全部試せます。ただ、いつも通り制約を見ますと、
1 <= n <= 40
です。「あれ、案外小さいぞ」と思ったのですが、計算してみると
2^40 ≃ 10^12
です。ちょっと厳しいですね。工夫しましょう。今回は「半分全列挙」という手法を用います。
小さい例を挙げて説明します。
「1,2,3,4」, t=8
を全パターン試しましょう。2^4=16通りあります。いきます。
0
1
2
3
4
1+2=3
1+3=4
1+4=5
2+3=5
2+4=6
3+4=7
1+2+3=6
1+2+4=7
1+3+4=8
2+3+4=9
1+2+3+4=10
ですね。出てきた数字をまとめると。
{0,1,2,3,4,5,7,6,8,9,10}
ですね。t=8ですので、答えは8と求まりました。
次に「半分全列挙」します。名前の通り半分にして全列挙します。
適当に半分にします。
「1,2,3,4」→「1,2」「3,4」
それぞれ、全パターン試します。
0
1
2
1+2=3
と
0
3
4
3+4=7
さて、いったんまとめます。
{0,1,2,3}
{0,3,4,7}
少し問題からは逸れますが、上と下の全ての組み合わせをとってみます。
0+0=0
0+3=3
0+4=4
0+7=7
1+0=1
1+3=4
1+4=5
1+7=8
2+0=2
2+3=5
2+4=6
2+7=9
3+0=3
3+3=6
3+4=7
3+7=10
まとめると、
{0,1,2,3,4,5,6,7,8,9,10}
です。分けない場合と同じものが実現されてますね。ただ、このままだと計算量は減ってません。
問題に戻ります。半分にしても同じものが実現されることが分かったので、計算量を減らしていきましょう。
まず、片方をソートします。今回は大丈夫ですね。説明のために片方の昇順を崩します。
t=8
{0,1,2,3}
{7,3,0,4}
ここから2分探索にて適切な値を求めていきます。と書きましたが、そんなに大変ではないです。
まず、ソートされていないほうから値を取り出します。「7」ですね。上の 集合から 7 とペアになっても t を超えない値をスマートに取り出します。
t - 7 = 8 - 7 = 7
ですので、1以下であれば大丈夫です。幸運なことに上の集合はソートされていますので、lower_boundやupper_boundを用いれば、あっという間に1以下の一番大きい数が取り出せます。
今回は 1 です。7 + 1 = 8 を保存しておきましょう。もし、2回目以降でしたら、大きいほうを取りましょう。
これを7->3->0-.>4と集合の要素全部で行います。
その中の最大値が答えです。
分けてあげることで、計算量は
2^20 ≃ 10^6
に落ちるので、なんとか間に合います(ソートやら探索がありますが、これよりは小さいです)。
さて、実装です。
と移りたいのですが、公式放送にて選択した値の和集合、
{0,1,2,3,4,5,7,6,8,9,10}
や
{0,1,2,3}
{0,3,4,7}
を簡単に作る方法が説明されていましたので紹介します。
まず
{0,1,2,3,4,5,7,6,8,9,10}
の作り方です。0だけの配列を用意して、「1,2,3,4」を頭から足したものを後ろに付け加えていきます。これだけです。

重複が生じますが問題ありません。これで、
{0,1,2,3,4,5,7,6,8,9,10}
が完成です。次は半分にしたものを作りましょう。
今回は0の配列を2つ用意します。上記の操作を1つ目の配列、2つ目の配列と交互に行えば分けた集合が完成します。

今までの説明では「1,2」「3,4」で分けましたが、この例だと「1,3」「2,4」で分けてます。統一したかったのですが、ここまで解説を書いてだいぶ疲れたので修正を諦めました。すみません。
さて、実装に移ります。
#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
using namespace std;
using P = pair<int, int>;
using ll = long long;
int main()
{
int n, t;
cin >> n >> t;
vector<int> a(n);
rep(i, n) cin >> a[i];
vector<ll> s1, s2;
s1 = s2 = { 0 };
//和の集合を作成
rep(i, n)
{
int m = s1.size();
rep(j, m)
{
s1.emplace_back(s1[j] + a[i]);
}
swap(s1, s2);
}
sort(s1.begin(), s1.end());
ll ans = 0;
for (auto x : s2)
{
if (x > t) continue;
int idx = upper_bound(s1.begin(), s1.end(), t - x) - s1.begin();
ans = max(ans, x + s1[idx-1]);
}
cout << ans << endl;
return 0;
}上記の説明において「集合」という言葉を重複を許したものにも用いていますが厳密には正しくありません。平易な言葉で表現するために、このような記述をしています。ご了承ください。
本問題は「半分全列挙」を知っているかどうかという点が重要でした。私は知りませんでした。でも、これで皆さんも理解できた、もしくは拙い説明のせいで理解できなくても、「こんな手法があったなー」という状態になったのではないのでしょうか。次は解けるはずです。
だいぶのんびり記事を書いてしまいました。abc184っていつやりましたっけ?
「UnionFindの記事書かなきゃ」と毎回言ってるように、アルゴリズムの説明を早く書かないとなーと思う日々です。そうすれば、本記事のように解説を書く際にも「eは幅優先!このページ見て!」とできるので更新速度が上がるはずです。いつか書きます。
この記事が気に入ったらサポートをしてみませんか?
